-
Články
- Časopisy
- Kurzy
- Témy
- Kongresy
- Videa
- Podcasty
Analýza dat v neurologii
L. Vybrané komentáře k odhadům a interpretaci poměru šancí
Autori: L. Dušek; T. Pavlík; Jiří Jarkovský
; J. Koptíková
Pôsobisko autorov: Masarykova univerzita, Brno ; Institut biostatistiky a analýz
Vyšlo v časopise: Cesk Slov Neurol N 2015; 78/111(2): 240-243
Kategória: Okénko statistika
Tento jubilejní díl seriálu budeme věnovat dílčím komentářům zaměřeným na vybrané problémy spojené s odhady šance (O) a poměru šancí (OR) v asociačních studiích. Uzavíráme tak kapitoly, na které nebyl dostatečný prostor v předchozích dílech seriálu, a také odpovídáme na nejčastější otázky, které v této souvislosti zaznívají v literatuře či na přednáškách.
Pro srozumitelnost v úvodu opakujeme nejjednodušší tabulku četností 2 × 2 s typickým značením četností v jednotlivých polích a, b, c, d (viz též díl seriálu 49) (tab. 1).
Tab. 1. Výpočet relativního rizika (RR) a poměru šancí (OR) na základě tabulky četností 2 × 2. 
Jak postupovat v případě, kdy se v tabulce četností objeví políčko s nulou?
Pro výpočet poměru šancí je tato situace vážnou komplikací, což je patrné již z výše uvedených vztahů pod tabulkou četností. Pokud nulová četnost nastane v buňkách b, c, pak poměr šancí nelze spočítat, neboť nemůžeme dělit nulou. Jsou‑li nulové buňky a, d, pak OR sice spočítat můžeme, ale nevyhnutelně vyjde nulové, což nedává interpretační smysl. Do publikací v obou případech píšeme poznámku „OR not defined due to zero cells in frequency table“. Nastane‑li taková situace, je třeba prověřit, zda skutečně jde o kategorie vzácné až nemožné, kde je nulová četnost objektivní fakt, anebo jde o chybu vzorkování. S takovou chybou se setkáváme především u malých vzorků, které snadno podhodnotí výskyt některé vzácnější kategorie.
Jak se u asociačních prospektivních a retrospektivních studií liší cílový parametr, end‑point?
V zásadě se neliší, oba experimentální plány sledují stejný cíl. Jednoduše řečeno, jde o to posoudit vliv expozice (tedy experimentálního zásahu, léčby, vliv nějakého znaku, prediktoru, rizikového faktoru) na výskyt zkoumaného jevu (typicky nemoci). Výskyt nemoci je tedy cílovým parametrem, přičemž ho měříme jako relativní četnost ve skupině exponovaných a neexponovaných jedinců. Rozdíl mezi prospektivním a retrospektivním plánem je pouze ten, že se na daný problém dívají z opačné strany. Pouze prospektivní plán ovšem umožňuje reprezentativní odhad prevalence zkoumaného jevu, proto je možné u něj odhadovat relativní riziko (RR) jeho výskytu. Retrospektivní plány již při zařazování jedinců do studie rozhodují o poměru případů a kontrol, relativní výskyt případů tedy není nezávislý odhad, ale výsledek náběru probandů.
Existuje nějaké jednoduché pravidlo, kdy použít OR a kdy RR?
Ano, existuje. Jak bylo vysvětleno v dílech 48 a 49 našeho seriálu, nejlepší doporučení jsou tato:
- RR nemá smysl a může být silně zavádějící u retrospektivních studií (studie případů a kontrol, retrospektivní kohortové studie); zde je naopak dobře interpretovatelný odhad OR.
- U prospektivních observačních studií (kohortové, průřezové) lze sice odhadnout OR i RR, z hlediska interpretace je ale lepší RR, neboť pracuje s reprezentativním odhadem rizika (pravděpodobnosti) výskytu jevu v exponované a neexponované skupině; to samé platí u prospektivních randomizovaných studií.
- Rovněž následné metaanalýzy, je‑li to možné, srovnávají preferenčně odhady RR. U studií, kde to jde, je možné hodnotu RR aproximovat (přepočítat) z odhadu OR (např. při splnění předpokladu vzácných onemocnění).
Proč je v literatuře stále častěji používán OR, a to i u prospektivních kohortových studií?
Důvodů je více. V první řadě můžeme uvést snadný způsob výpočtu a jeho dobrou dostupnost v běžných softwarových nástrojích. Více sofistikovaný důvod je, že odhad OR je běžný výstup složitějších modelovacích technik, které jsou velmi efektivní pro hodnocení komplikovaných tabulek četností. Zejména jde o logistickou regresi, které se budeme věnovat v některém z dalších dílů našeho seriálu. Tato modelovací technika umožňuje odhady i vícerozměrně adjustovaného poměru šancí, a tedy odfiltrování současného vlivu více zavádějících faktorů. Právě proto bývá využívána i pro kohortové prospektivní studie.
Odhad OR má také řadu dalších numerických výhod, které ho často favorizují před RR. Například platí následující vztah:
- ORriziko = 1/ORprotekce nebo jiným označením ORneúspěch = 1/ ORúspěch
Jinými slovy jednoduchou inverzí můžeme přepínat odhad OR pro hodnocení neúspěchu nebo úspěchu, a to nejen vlastní bodový odhad OR, ale i hraniční hodnoty jeho intervalu spolehlivosti. Výhodou je, že můžeme velmi lehce měnit interpretaci stejného odhadu z pohledu rizikovosti nebo naopak protekce dané sledovaným faktorem. Při publikaci výsledků, kde zpracováváme více odhadů OR, pak můžeme snadno nastavit jejich „směr“ tak, aby vypovídaly konzistentně. Odhad RR takovou vlastnost nemá, a tudíž musíme již při primárním výpočtu velmi pozorně sledovat, zda hodnotíme „úspěch“ či „neúspěch“, nebo „rizikový vliv faktoru vs. protektivní vliv faktoru“. Ukázku takových recipročních výpočtů dokumentujeme na příkladu 1.
Příklad 1. Ukázka recipročního přepočtu poměru šancí a relativního rizika v asociační studii. 
V příkladu 2 dále popisujeme situaci, kdy hodnotíme asociaci více potenciálních prediktorů vůči cílovému parametru „nemoc: ano/ ne“. Hodnotíme tedy více tabulek četností a výsledkem je více odhadů OR. Pro čtenáře je vhodné a přehledné, pokud zkoumané prediktivní faktory mají stejný „směr“, tudíž vyjadřují buď rizikový, nebo naopak protektivní účinek. Toto sladění provedeme u odhadů OR velmi snadno pomocí výše uvedeného vztahu mezi OR pro úspěch a OR pro neúspěch. Příklad 2 také dokumentuje, že stejně lze postupovat i u hranic intervalu spolehlivosti.
Příklad 2. Přepočet hodnot poměru šancí (OR) z „šance protekce“ na „šanci rizika“. 
Je možné jednoduše srovnat hodnoty RR a OR? A za jakých situací?
Zjednodušeně shrnuto má takové přímé srovnání smysl v podstatě jen ve dvou modelových situacích:
- U retrospektivních studií (typicky studie případů a kontrol) při platnosti předpokladu vzácného onemocnění (viz díl 48 a 49 seriálu), kdy lze hodnotu OR aproximovat na RR.
- U prospektivních studií (typicky observační kohortové nebo průřezové studie, případně i randomizované klinické studie), kde můžeme současně odhadovat RR i OR; v takovém případě:
- hodnoty OR a RR se absolutně shodují pouze v případě, kdy žádná asociace mezi zkoumaným jevem a expozicí neexistuje, potom platí OR = RR = 1,
- hodnoty OR jsou vždy extrémnější (tj. vzdálenější od hodnoty 1, a to oběma směry) než odpovídající hodnoty RR; tento rozdíl narůstá s rostoucí prevalencí zkoumaného znaku ve zdrojové tabulce četností – u běžně se vyskytujících znaků (prevalence větší než 5 – 10 %) nelze odhady RR a OR vzájemně zaměňovat.
V jakém vztahu je odhad rizika a odhad šance?
V literatuře je většinou pojednáváno o srovnání a vzájemné aproximaci OR a RR (viz odstavec výše). Srovnání šance výskytu jevu A (OA) a rizika jevu A (PA) je ale stejně důležité. Připomeňme, že rizikem zde označujeme pravděpodobnost nastání nějakého jevu či události. Šance nastání jevu a jeho riziko ve smyslu pravděpodobnosti jsou vzájemně spojeny již definičním vztahem:
- OA = PA/ (1 – PA), a tedy recipročně PA = OA/ (1 + OA).
Z těchto vztahů opět vidíme, že u vzácných jevů, kde je PA nízké, bude hodnota OA blízká až rovna hodnotě PA. U běžných jevů budou hodnoty číselně nesouměřitelné, neboť platí:
- PA je pravděpodobnost, a tudíž může nabývat hodnot pouze v intervalu 0 až 1;
- naopak OA nabývá hodnot od 0 až do nekonečna.
Výše uvedené omezení možných hodnot rizika (PA) se následně promítá i do omezení rozsahu hodnot poměru rizik, tedy relativního rizika RR. Relativní riziko je totiž poměrem rizik, tedy pravděpodobností, a ty jsou limitovány rozsahem možných hodnot 0 až 1. Tudíž i hodnoty RR jsou omezeny, a proto také hodnoty OR vycházejí „extrémněji“, tedy jsou číselně vzdálenější od referenční hodnoty 1 než hodnoty RR. Uvažujme hodnotu rizika v kontrolní skupině stejnou jako v příkladu 1, tedy 0,4. Potom je maximální možná vypočtená hodnota RR = 2,5, protože riziko v čitateli poměru RR nemůže překročit 1, a tedy 1/ 0,4 = 2,5. Hodnota rizika v kontrolní skupině tak determinuje maximální možnou hodnotu RR; s klesajícím rizikem v kontrolní skupině roste maximální možná hodnota RR. Hodnoty poměru šancí takové omezení nemají. Srovnání různých hodnot RR a OR uvádíme v tab. 2, ze které je patrné, že:
- s rostoucí prevalencí sledovaného rizikového jevu narůstá rozdíl mezi OR a RR; OR je přitom vždy vzdálenější od hodnoty 1;
- i v případě, kdy je hodnota RR téměř rovna 1, může OR nabývat hodnoty > 1;
- hodnota OR na rozdíl od RR souvisí s absolutním rozdílem rizika mezi kontrolní a experimentální skupinou, s rostoucí diferencí rizik roste i OR;
- RR nesouvisí s absolutním rozdílem rizik; tedy i při stejné absolutní diferenci rizika mezi kontrolní a experimentální skupinou může RR nabývat různých hodnot.
Tab. 2. Srovnání různých odhadů relativního rizika (RR) a poměru šancí (OR) z asociačních tabulek četností 2 x 2. 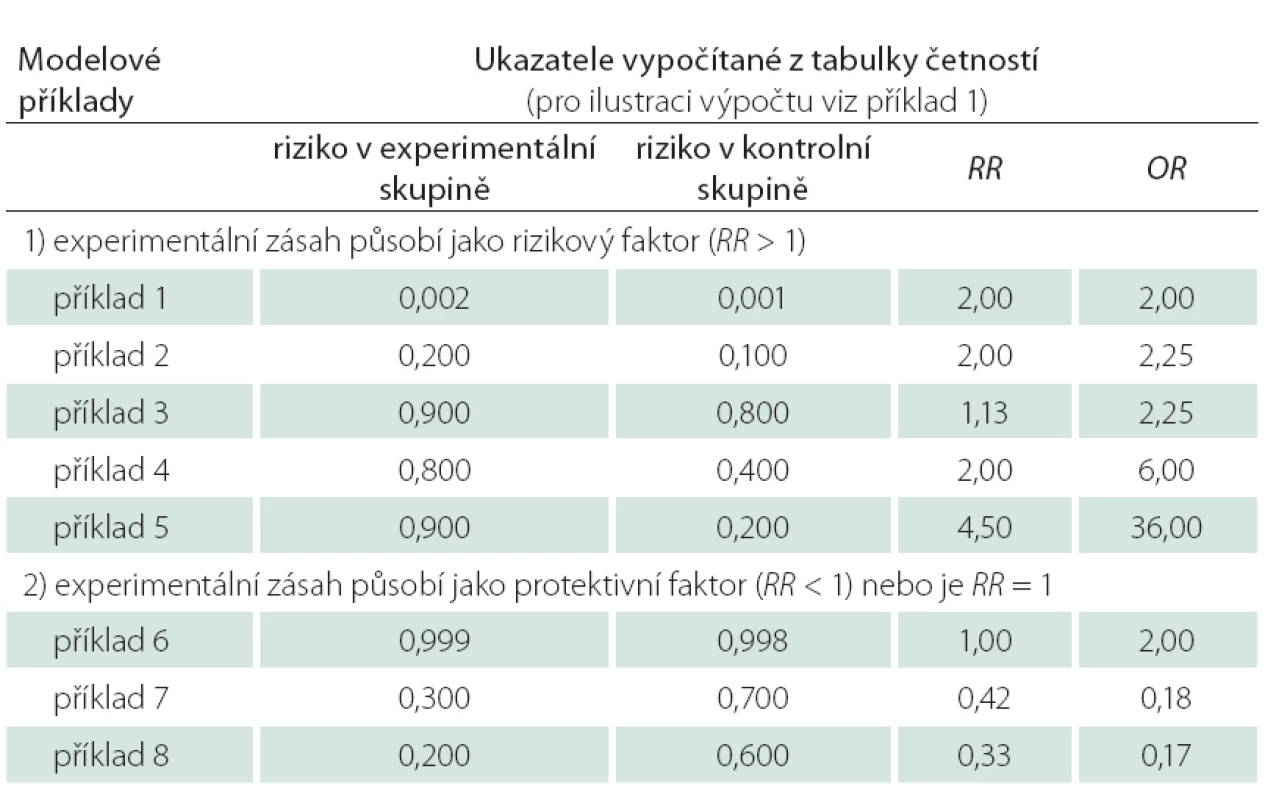
Modelové příklady odvozené z prospektivních kohortových studií, u kterých lze smysluplně hodnotit RR i OR. Velký číselný rozsah možných hodnot OR (tj. od 0 až do nekonečna) představuje problém při vzájemném srovnávání výstupů různých studií. Pro tento účel existují standardizované postupy, díky kterým je interpretace hodnot OR snazší. Tomuto problému se budeme věnovat v příštím díle seriálu.
doc. RNDr. Ladislav Dušek, Ph.D.
Institut biostatistiky a analýz
MU, Brno
e‑mail: dusek@iba.muni.cz
Štítky
Detská neurológia Neurochirurgia Neurológia
Článek Projekt ncRNAPainČlánek Webové okénkoČlánek Neuromyelitis opticaČlánek Agresivní hemangiom obratleČlánek Registr mechanických rekanalizací u akutního iktu – pilotní výsledky multicentrického registruČlánek Recenze knih
Článok vyšiel v časopiseČeská a slovenská neurologie a neurochirurgie
Najčítanejšie tento týždeň
2015 Číslo 2- Metamizol jako analgetikum první volby: kdy, pro koho, jak a proč?
- Kombinace metamizol/paracetamol v léčbě pooperační bolesti u zákroků v rámci jednodenní chirurgie
- Neuromultivit v terapii neuropatií, neuritid a neuralgií u dospělých pacientů
- Antidepresivní efekt kombinovaného analgetika tramadolu s paracetamolem
-
Všetky články tohto čísla
- Neuromyelitis optica
- Radiologické hodnocení lumbální spinální stenózy a jeho klinická korelace
- Agresivní hemangiom obratle
- Použití antipsychotik u nemocných s demencí
- Skrat u karotických endarterektomií zvyšuje riziko ischemického iktu
- Chirurgická léčba laterální bederní stenózy perkutánně zavedeným interspinózním implantátem
- Chirurgický přístup k tumorům thalamu
- Možnosti ovlivnění diplopie při paralytickém strabizmu konzervativní léčbou
- Dotazník funkcionální komunikace (DFK) – validace originálního českého testu
- Rozdiely medzi pohlaviami v klinických prejavoch a výskyte porúch spánku u pacientov s Parkinsonovou chorobou – populačná štúdia
- Penilní vibrostimulace u pacientů s míšním poraněním
- Registr mechanických rekanalizací u akutního iktu – pilotní výsledky multicentrického registru
- Progredující demence s parkinsonizmem a poruchami chování – od prvních příznaků k neuropatologické diagnóze (kazuistika)
- Projekt ncRNAPain
- Kongenitální centrální hypoventilační syndrom (Ondinina kletba)
- Neurologická komplikace hepatitidy E – kazuistika
- Neurologické projevy Behçetovy nemoci – kazuistika
- Úspešne liečená depresia u pacienta s epilepsiou – kazuistika
- Zánětlivý pseudotumor imitující intrakraniální, konvexitární meningeom – kazuistika
- Odešel prof. MU Dr. Jiří J. Vítek (29. 3. 1935– 19. 12. 2014)
- Padesát let prof. MU Dr. Milana Brázdila, Ph.D., FCMA
- Webové okénko
-
Analýza dat v neurologii
L. Vybrané komentáře k odhadům a interpretaci poměru šancí - Recenze knih
- Česká a slovenská neurologie a neurochirurgie
- Archív čísel
- Aktuálne číslo
- Informácie o časopise
Najčítanejšie v tomto čísle- Agresivní hemangiom obratle
- Neuromyelitis optica
- Kongenitální centrální hypoventilační syndrom (Ondinina kletba)
- Radiologické hodnocení lumbální spinální stenózy a jeho klinická korelace
Prihlásenie#ADS_BOTTOM_SCRIPTS#Zabudnuté hesloZadajte e-mailovú adresu, s ktorou ste vytvárali účet. Budú Vám na ňu zasielané informácie k nastaveniu nového hesla.
- Časopisy



