-
Články
- Časopisy
- Kurzy
- Témy
- Kongresy
- Videa
- Podcasty
Analýza dat v neurologii VI.
Přesnost, spolehlivost a reprodukovatelnost měření u diskrétních dat
Autori: L. Dušek; T. Pavlík; J. Koptíková
Pôsobisko autorov: Institut biostatistiky a analýz, Masarykova univerzita, Brno
Vyšlo v časopise: Cesk Slov Neurol N 2007; 70/103(6): 719-721
Kategória: Okénko statistika
Termíny uvedené v nadpisu článku se do jisté míry staly zaklínadly moderního vědeckého bádání. Cílový stav se tedy zdá být nastaven, neboť všechny tyto atributy by v ideálním výzkumu měly být na maximu. Skutečnost je ale vždy o něco slabší něž teorie a hlavně je závislá na badateli, který plánuje a řídí výzkum. Jelikož hodnocení reprodukovatelnosti je nutnou součástí klinických výzkumů, rozhodli jsme se věnovat této problematice dva díly našeho statistického seriálu. Tento první řeší problematiku nespojitých dat, tedy binárních kódů a kategoriálních skóre. V příštím díle rozebereme obdobné hodnocení u spojitých dat a v některé z následujících částí se zaměříme na analýzu spolehlivosti diagnostických testů.
Tato část výkladu analýzy dat není příliš záživná, nicméně přesto prosíme laskavé čtenáře o trpělivost. Jde o analýzy, které bývají v kratších učebnicích opomíjeny a také běžně dostupné statistické programy jim nevěnují správnou míru pozornosti. Výsledkem je někdy dost limitující nezkušenost a neznalost. Nedostatečná nebo nedoložená opakovatelnost výsledků experimentu může být příčinou zamítnutí publikace v dobrém časopise nebo může značně zkomplikovat obhajobu řešených projektů. Přitom řešení není nijak složité a v zásadě 4-5 jednoduchých testů nás zbaví většiny problémů tohoto typu. Pro přesnost, spolehlivost i reprodukovatelnost dnes existují exaktní metody hodnocení a kvantifikace. Nejde tedy jen o kvalitativní atributy. Nejprve ale stručně probereme význam a podstatu klíčových pojmů.
- Reprezentativnost je velmi významným předpokladem smysluplného vědeckého bádání. Je jistě důležité aby to, na čem měříme, odpovídalo tomu, o čem chceme hovořit. Jde tedy o faktor vztahující se k samotnému počátku výzkumu, k plánování a náběru vzorku. Vzorkovací plány mohu být různé podle typu měřeného znaku a hodnocené populace. Samostatnou kapitolou, ke které v našem seriálu také dospějeme, je náběr pacientů do různých typů srovnávacích klinických studií. Není-li vzorek reprezentativní pro daný účel a cíl výzkumu, pak jakékoli měření postrádá smysl a nutně vede ke zkresleným („biased“) závěrům.
- Přesnost je parametr, který se vztahuje k výsledkům měření anebo k výsledkům odhadování statistických ukazatelů. Je to údaj přímo vypovídající o kvalitě naší práce. Všechny běžně používané statistické ukazatele (např. průměr nebo medián) hodnotíme odhadem, což je statistická metoda vedoucí k přibližnému určení neznámých parametrů statistického (základního) souboru. Je samozřejmé, že odhady získané měřením náhodného vzorku se od skutečné hodnoty základního souboru odchylují. Přesnost odhadu je potom vyjádřením velikosti této odchylky.
- Spolehlivost je pojem úzce související s přesností, přesné odhady jsou rovněž spolehlivé. Spolehlivost má ale vyšší význam a zavádí do systému pravděpodobnostní interpretaci. Spolehlivost vyjadřujeme intervalem spolehlivosti, který určuje pravděpodobnostní hranice pro výsledky opakovaných měření téhož experimentu. Správná interpretace například 95% intervalu spolehlivosti pro aritmetický průměr je následující: opakujeme-li nezávisle odhad průměru na téže populaci, pak v 95 % opakování budou získané odhady ležet uvnitř intervalu spolehlivosti.
- Přesnost přímo souvisí se spolehlivostí, ale nezajistí reprezentativnost. Můžeme velmi přesně odhadnout zcela nereprezentativní hodnoty. Těmto aspektům se budeme věnovat v příštím díle tohoto seriálu.
- Reprodukovatelnost a opakovatelnost definujeme jako míru shody, které dosáhneme u výsledků opakovaného experimentu, pokud je tento prováděn za stále stejných podmínek, na stejném zařízení apod. Velmi lapidárně řečeno, zařízení a podmínky zůstávají a experiment je nezávisle opakován. Mění se tedy materiál a podle okolností experimentátor (dotazovatel, expert apod).
Význam pojmů reprodukovatelnost a opakovatelnost
Jistě není třeba vysvětlovat, že reprodukovatelnost výsledků je jedním z nosných pilířů vědeckého bádání. Pouze reprodukovatelně měřitelné hodnoty mohou být součástí závazných diagnostických testů a autoři klinických publikací jsou často vyzýváni, aby reprodukovatelnost číselně doložili. Přitom často ne zcela správně synonymicky splývají pojmy „reproducibility“ a „repeatability“. Reprodukovatelnost je jednoznačně vyšší pojem, neboť vypovídá o opakovatelnosti nezávisle potvrzené různými lidmi nebo týmy. Opakovatelnost sama je mírou shody po sobě provedených experimentů, kde nutně není měněn experimentátor. Čistě teoreticky tak můžeme mít obtížně opakovatelné experimenty, které se ne vždy zdaří, ale jsou reprodukovatelné, neboť je úspěšně provedly různé týmy po celém světě. Jako příklad uveďme např. klonování zvířat.
V odborné literatuře často nalezneme popis reprodukovatelnosti a opakovatelnosti výsledků pod pojmy „interobserver“ a „intraobserver“ variabilita. Při opakovaném měření různými odborníky můžeme analyzovat rozdíly mezi nimi, i shodu měření v rámci jednotlivých pozorovatelů nebo experimentátorů. V běžném hodnocení naměřených dat ovšem častěji analyzujeme opakovatelnost, nicméně stejné statistické postupy jsou využitelné i pro reprodukovatelnost. Provedeme-li experiment s jednou myší, budeme další opakování dělat s jinými zvířaty a shoda výsledku rozhodne o opakovatelnosti.
Oba typy hodnocení do značné míry závisí na typu měřených znaků. Pro spojité znaky můžeme zapojit jakoukoli metodu, která hodnotí různé zdroje rozptylu, včetně vlivu experimentátora nebo různých experimentátorů. Rozptyl je přitom logicky protikladem opakovatelnosti, čím je větší, tím jsou výsledky náhodnější a v určité chvíli je již nelze prohlásit za reprodukovatelné. Reprodukovatelnost i opakovatelnost mají blízko ke spolehlivosti a jejich mírou mohou být i již výše zmíněné intervaly spolehlivosti. Jinak ale tato hodnocení vyžadují u spojitých dat více sofistikované postupy jako je korelační analýza, analýza rozptylu nebo ROC analýza. Těmto metodám se budeme věnovat později, zde se blíže zaměříme pouze na hodnocení opakovatelnosti u nominálních a kategoriálních znaků.
Míry reprodukovatelnosti a opakovatelnosti u nominálních a kategoriálních znaků
Nominální i kategoriální znaky statisticky sumarizujeme frekvenčními tabulkami, kde vyjadřujeme četnosti jednotlivých kategorií znaku(ů). Z tohoto důvodu také míry reprodukovatelnosti i opakovatelnosti pracují s frekvenčními daty a sledují míru shody v četnostech konkrétních kategorií. Jedním z nejčastěji používaných ukazatelů shody dvou nebo více opakovaných kategoriálních měření je tzv. koeficient kappa. Výpočet kappa doložíme přímo na příkladu v tabulce 1, která shrnuje prediktivní hodnocení vývoje nemoci u 29 pacientů od dvou lékařů.
Tab. 1. Srovnání hodnocení dvou posuzovatelů pomocí koeficientu kappa. 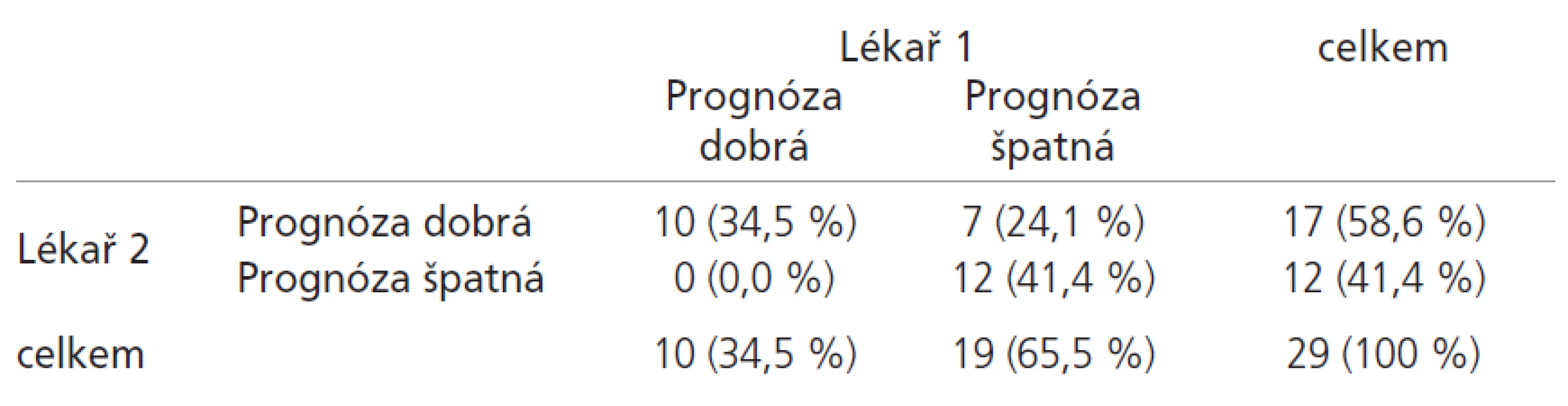
Je zřejmé, že počet shodných hodnocení obou lékařů (10 + 12 = 22 pacientů) se nemusí rovnat počtu ostatních kombinací a podíl shodných měření tak může být ovlivněn počtem subjektů zařazených do řádků nebo sloupců tabulky. Abychom čtenáře nezatěžovali složitým vzorcem, uvádíme výpočet přímo na číslech z tabulky:
Kappa = (podíl dosažené shody – podíl náhodné shody)/(1 - podíl náhodné shody)
kde
- podíl dosažené shody je (10 + 12) / 29 = 0,759
- podíl náhodné shody je (0,586*0,345) + (0,414*0,655) = 0,473
- a tedy kappa = (0,760 – 0,474) / (1 – 0,474) = 0,543
Smysl existence kappa vyplývá již z výpočtu. Jde o objektivní míru srovnávající podíl skutečně dosažené shody po odečtení vlivu shody, které by bylo dosaženo náhodně. Tímto kappa nahrazuje prostý podíl shodných hodnocení. Podíl shodných odpovědí je totiž ovlivněn rozložením počtu odpovědí v jednotlivých částech tabulky. Koeficient kappa říká, jaký podíl z maximálně možné shody byl dosažen nad rámec shody zcela náhodné. Kappa > 0 ukazuje na větší podíl shody než při shodě zcela náhodné, kappa = 1 potom znamená absolutní shodu v odpovědích. Kappa ovšem může být i 0 (zcela náhodná shoda) anebo menší než 0, pak jde o míru shody nižší než náhodnou. Možné aplikace koeficientu kappa jsou následující:
- hodnocení shody mezi hodnocením dvou a více lékařů
- u dotazníkových průzkumů hodnocení shody u výpovědí různých respondentů
- při opakovaném dotazování hodnocení shody výpovědí u stejných jedinců
Koeficient kappa může být kalkulován podle výše uvedeného vzorce jako tzv. nevážený výpočet („unweighted kappa“) anebo je možné dodat ke kombinacím kategorií váhy. Potom hovoříme o tzv. váženém výpočtu kappa. Význam váženého výpočtu nastupuje především u tabulek s větším počtem kategorií. Zde totiž závažnost shody nebo neshody pozorovatelů závisí i na vzdálenosti (nebo významu) kategorií a jejich empirické vážení může výpočet přiblížit praxi. Zájemce o metodiku výpočtu odkazujeme na práce Cohen (1960) nebo Fleiss (1981). Zde lze také nalézt vzorce standardní chyby i intervalů spolehlivosti pro odhad kappa.
Zcela pragmaticky ovšem platí, že výpočet kappa bývá nasazován především v situacích, kdy je míra shody vyšší než náhodná a analytik chce ověřit spíše velikost shody než samotnou odchylku kappa od 0. Přitom ale neexistuje všeobecný konsensus pro kategorizaci hodnot kappa. Hodnoty kappa menší než 0,20 bývají hodnoceny jako velmi nízké, v rozsahu 0,21–0,40 jsou interpretovány jako spíše slabá míra shody, hodnoty v rozsahu 0,41–0,60 jako průměrná shoda a nad 0,6 jako nadprůměrná shoda (viz např. Altman, 1998).
Abychom byli korektní, musíme podotknout, že koeficient kappa není jako míra opakovatelnosti bez problémů a má v literatuře své silné kritiky. Výpočtu je vytýkáno, že vychází z teoretických předpokladů, které netestuje (např. výpočet podílu náhodné shody), dále nijak neseparuje různé varianty neshody a shodu agreguje do jediného podílu. Všechny nedostatky jsou více viditelné u větších tabulek s více kategoriemi hodnot.
Interpretační význam koeficientu kappa se tedy nesmí přeceňovat. Kappa je pouze mírou shody dvou nebo více pozorovatelů. Tento test je vhodné dále doplnit analýzou možného systémového zkreslení ve výpovědích pozorovatelů, tedy testem na tzv. „interobserver bias“. Pro analýzu takových vícečetných hodnocení je ideální Cochranův Q test, který sleduje zda pravděpodobnost určitého hodnocení zůstává přes všechny provedené experimenty mezi pozorovateli stejná.
Tab. 2. Příklad dat pro Cochranův Q test při srovnání hodnocení od pěti posuzovatelů. 
* 1 = nepříznivá prognóza vývoje nemoci; 0 = dobrá prognóza vývoje nemoci.
** data pacienta č. 2 nejsou zařazena do výpočtu, neboť u něj nastala shoda všech lékařů
Vzorová vstupní data pro výpočet Cochranova Q jsou uvedena v tabulce 2 (modifikováno z publikace Zar, 1999). Je patrné, že jde o test celkového zkreslení výstupů některým z pozorovatelů. Odborně hovoříme o testu homogenity u vícečetných opakovaných měření („repeated-measures experimental design“). Vzorec pro výpočet zde neuvádíme, je příliš složitý a výpočet je nadto dostupný v běžných softwarových programech. Výsledkem příkladu v tabulce 2 je potvrzení nulové hypotézy. Nelze tedy prokázat významný rozdíl v podílu nepříznivých hodnocení mezi lékaři a systémové zkreslení výsledků tedy není pravděpodobné.
Závěrem. Analýza reprodukovatelnosti má své standardy a statistiky, které u kategoriálních dat nejde nahradit prostým odečtením podílu shodných odpovědí. K podobnému závěru dospějeme i v následující části věnované této problematice u spojitých znaků.
doc. RNDr. Ladislav Dušek, Dr.
Institut biostatistiky a analýz,
Masarykova univerzita, Brno
e-mail: dusek@cba.muni.cz
Zdroje
1. Altman DG. Some common problems in medical research. In: Practical Statistics for Medical Research. 8th ed. London: Chapman & Hall 1998 : 403-9.
2. Cohen JA. A coefficient of agreement for nominal scales. Educ Psychol Meas 1960; 20 : 37–46.
3. Fleiss JL. Statistical methods for rates and proportions. 2nd ed. New York: John Wiley 1981 : 38-46.
4. Zar JH. Biostatistical Analysis. 4th ed.. New Jersey: Prentice Hall 1999.
Štítky
Detská neurológia Neurochirurgia Neurológia
Článek Obrna lícního nervuČlánek Webové okénko
Článok vyšiel v časopiseČeská a slovenská neurologie a neurochirurgie
Najčítanejšie tento týždeň
2007 Číslo 6- Metamizol jako analgetikum první volby: kdy, pro koho, jak a proč?
- Kombinace metamizol/paracetamol v léčbě pooperační bolesti u zákroků v rámci jednodenní chirurgie
- Neuromultivit v terapii neuropatií, neuritid a neuralgií u dospělých pacientů
- Antidepresivní efekt kombinovaného analgetika tramadolu s paracetamolem
- CIDP: epidemiológia, klinický obraz a diagnostika v kocke
-
Všetky články tohto čísla
- Obrna lícního nervu
- Elektrofyziologické vyšetření lícního nervu
- Protilátky proti glykokonjugátům v diagnostice autoimunitních neuropatií
- 5 let činnosti Národní referenční laboratoře lidských prionových onemocnění při Oddělení patologie a molekulární medicíny FTNsP: naše zkušenosti a přehled literatury
- Klinický pohled na výpočetní tomografii u akutní ischemie mozku
- Ultrazvukové hodnocení substantia nigra u pacientů s parkinsonskými syndromy
- Porovnání výsledků vyšetření zrakových evokovaných potenciálů u pacientů s roztroušenou sklerózou a neuroboreliózou
- Kognitívne evokované potenciály – vlna P300 u pacientov so sclerosis multiplex: vzťah k forme ochorenia, somatickému postihnutiu a kvalite života
- Relabující-remitující roztroušená skleróza a oligoklonální pruhy v průběhu léčby modifikující průběh choroby
- Mozková žilní trombóza u uživatelek hormonální antikoncepce
- Úspěšné použití jediné otázky pro screening syndromu neklidných nohou v České republice
- Závisí vývoj dysfunkce mikce u roztroušené sklerózy na typu neurologické léčby?
- Poruchy polykání ve vztahu k vertebrogenním dysfunkcím
- Centrální neurocytom: kazuistika a přehled literatury
- Gelastické záchvaty u hypotalamického hamartomu: kazuistika
- Dercumova choroba (lipomatosis dolorosa) – zriedkavo diagnostikované ochorenie: kazuistika
- Poúrazová porucha čichu: kazuistiky
- K šedesátinám doc. MUDr. Martina Bojara, CSc.
-
Směruje použití mediánu ke statistickým neparametrickým postupům zpracování dat?
Okénko statistika – Analýza dat v neurologii – III.
Nebojme se mediánu a robustních statistik - Webové okénko
-
Analýza dat v neurologii VI.
Přesnost, spolehlivost a reprodukovatelnost měření u diskrétních dat
- Česká a slovenská neurologie a neurochirurgie
- Archív čísel
- Aktuálne číslo
- Informácie o časopise
Najčítanejšie v tomto čísle- Obrna lícního nervu
- Poruchy polykání ve vztahu k vertebrogenním dysfunkcím
- Protilátky proti glykokonjugátům v diagnostice autoimunitních neuropatií
- Dercumova choroba (lipomatosis dolorosa) – zriedkavo diagnostikované ochorenie: kazuistika
Prihlásenie#ADS_BOTTOM_SCRIPTS#Zabudnuté hesloZadajte e-mailovú adresu, s ktorou ste vytvárali účet. Budú Vám na ňu zasielané informácie k nastaveniu nového hesla.
- Časopisy



