-
Články
- Časopisy
- Kurzy
- Témy
- Kongresy
- Videa
- Podcasty
Analýza dat v neurologii
XXXV. Rozlišujme poměr šancí a relativní riziko
Autori: L. Dušek; T. Pavlík; Jiří Jarkovský
; J. Koptíková
Pôsobisko autorov: MU, Brno ; Institut biostatistiky a analýz
Vyšlo v časopise: Cesk Slov Neurol N 2012; 75/108(5): 642-645
Kategória: Okénko statistika
Tento díl seriálu věnujeme velmi častým výpočtům prováděným na základě tabulek četností, tedy odhadům poměru šancí (odds ratio) a relativního rizika (relative risk). Oba pojmy jsou v lékařské literatuře natolik zdomácnělé, že je ani nelze považovat za čistě biostatistické. Naším cílem je především vysvětlit interpretaci těchto pojmů, kterou nelze zaměňovat. Odhady poměru šancí a relativního rizika se spolu setkávají zejména v epidemiologických studiích, které zkoumají asociaci mezi rizikovými či ochrannými faktory a výskytem nemocí. Zjišťujeme, zda přítomnost nebo množství určitého faktoru zvyšuje riziko vzniku nemoci, nebo naopak jejímu vzniku zabraňuje. Někdy také hovoříme o expozici populace daným faktorem a zkoumáme její vliv na výskyt nemoci či jiného jevu. Typicky jde o studie observační (popisné nebo analytické), které pouze zaznamenávají výskyt sledovaných jevů a běh událostí nijak aktivně neovlivňují. V terminologii těchto studií často hovoříme o populaci exponované zkoumaným faktorem a o populaci neexponované. Opakem jsou studie intervenční, které ve svém plánu aktivně kontrolují jednotlivé zařazené jedince a přímo nastavují expozici zkoumaným faktorům. Tyto studie souhrnně označujeme jako experimentální.
V dalším textu se zaměříme výhradně na studie observační, jejichž typickým výstupem jsou tabulky četností, kde zaznamenáváme vztah (asociaci) mezi expozicí daným faktorem a výskytem nemoci nebo četností jiné změny zdravotního stavu sledovaných osob. V klinické praxi jsou typické asociační tabulky, do kterých zadáváme přímo individuální data jednotlivých osob, např. kouření (ano/ne) vs dýchací problémy (ano/ne). Relativní riziko a poměr šancí lze odhadnout různými výpočetními metodami, my zde principy vysvětlíme na nejjednodušším příkladu analýzy tabulky četností 2 × 2 (tzv. čtyřpolní tabulka četností). Budeme řešit situaci, kdy přítomnost určitého faktoru i sledovaný zdravotní stav vyjadřujeme jako binární veličiny (výskyt ano/ne). Schematicky tento typ záznamů představujeme v příkladech 1 a 2.
Pojem šance je často používán i v běžné mluvě, kde takto formou poměru hodnotíme možnou pravděpodobnost nastání nějakého jevu. Například šance na výhru v zápase 1 : 4 (jedna ku čtyřem) nebo šance uhodnutí určitého výsledku 1 : 9. Šance 1 : 4 se vztahuje k jevu, který nastane s pravděpodobností 1/(1 + 4) = 1/5, tedy 0,20; obdobně šance 1 : 9 odráží jev s pravděpodobností 0,10. Šanci jevu A značíme O(A) (odds) a definujeme ji jako podíl pravděpodobnosti nastání jevu A k pravděpodobnosti jevu opačného, tedy nenastání jevu A. Šanci ve prospěch A tedy vyjádříme jednoduchým vztahem:
P(A)
O(A) = -------------- -
1 – P(A)Šance výskytu jevu ve dvou populacích nebo v jinak definovaných skupinách osob (kohortách) lze dávat do poměru, potom hovoříme o poměru šancí (odds ratio = OR). Ten může nabývat nejnižší hodnoty 0, v maximu nijak ohraničen není. Vyjadřuje jednoduše, kolikrát je větší šance výskytu sledovaného jevu (např. nemoci) ve skupině osob exponovaných studovaným faktorem než ve skupině kontrolní (neexponované studovaným faktorem).
Rovněž pojem riziko (risk) je zcela běžný a stejně jako šance vyjadřuje pravděpodobnost nastání nějakého jevu či události. Lépe řečeno pravděpodobnost nějakého nezdaru či selhání, nejčastěji vzniku choroby. Absolutní riziko je pravděpodobnost výskytu dané nemoci ve sledované populaci. Tzv. rozdíl rizik (někdy také označován jako atributivní riziko) odráží přímý vliv expozice studovaným faktorem na výskyt nemoci a počítá se jednoduše jako rozdíl pravděpodobností výskytu nemoci ve skupině ovlivněné faktorem a ve skupině bez tohoto ovlivnění. Relativní riziko (RR) je pravděpodobnostní poměr vyjadřující míru asociace mezi ovlivňujícím faktorem a studovanou nemocí: RR = PE / PNE, kde PE je pravděpodobnost výskytu sledovaného jevu (vzniku nemoci) ve skupině exponovaných a PNE je pravděpodobnost výskytu stejného jevu v kontrolní skupině. Z definice vyplývá, že relativní riziko nevyjadřuje pravděpodobnost, ale poměr pravděpodobností ve dvou skupinách osob:
RR = 1 znamená, že expozice sledovaným faktorem neovlivňuje vznik onemocnění.
RR > 1 znamená, že expozice sledovaným faktorem zvyšuje riziko vzniku nemoci, jde tedy o rizikový faktor.
RR < 1 znamená, že expozice sledovaným faktorem snižuje riziko vzniku nemoci, a daný faktor je tedy protektivní.
Relativní riziko je tedy poměrem pravděpodobností, vyjadřujícím kolikrát je větší pravděpodobnost výskytu sledovaného jevu (vzniku nemoci) ve skupině ovlivněné studovaným faktorem (ve skupině exponovaných) ve srovnání se skupinou neexponovaných jedinců. Definičně jde o poměr dvou podmíněných pravděpodobností, neboť vztahuje pravděpodobnost vzniku nemoci při expozici faktorem k pravděpodobnosti vzniku nemoci bez expozice.
Je zřejmé, že poměr šancí i relativní riziko formou poměru srovnávají pravděpodobnost výskytu určitého jevu ve dvou různých skupinách osob. Oba ukazatele jsou si blízké i způsobem výpočtu, neboť je lze v nejjednodušším případě získat ze stejné čtyřpolní tabulky četností, jak ukazují příklady 1 a 2. Zmíněné příklady zároveň schematicky dokládají typický výstup observačních klinických nebo epidemiologických studií, které studují vliv určitého faktoru na výskyt nemoci v populaci. Čtenáře jistě napadne, že tabulku četností 2 × 2 uvedenou v příkladech 1 a 2 by bylo možné vyhodnotit testem dobré shody nebo Fisherovým exaktním testem (viz díly XX–XXII našeho seriálu). Nasazení těchto testů by rozhodně nebylo chybné. Oba testy hodnotí nulovou hypotézu o nezávislosti výskytu sledovaných jevů (zde expozice vs výskyt nemoci), avšak neumožňují existující vztah kvantifikovat. A právě pro kvantifikaci těsnosti (síly) sledovaného vztahu lze poměr šancí nebo relativní riziko použít.
Z příkladů 1 a 2 ovšem také vyplývá, že poměr šancí a relativní riziko se kalkulují různě a nelze je zaměňovat. Odpověď na otázku, proč tomu tak je, nás dovede k původnímu plánu (designu) studií, které k výsledným záznamům četností vedly. Jen tak totiž pochopíme, jakým výběrem zkoumaných osob tabulky četností vznikly. Nejjednodušší hledisko pro třídění observačních studií je hledisko časové, které dělí studie na prospektivní, retrospektivní a studie průřezové. Ačkoli tato klasifikace není zcela jednoznačná, vymezuje velmi instruktivně, jakým způsobem jsou nabíráni exponovaní a kontrolní jedinci, což je pro další výpočty rozhodující.
U prospektivních studií zjišťujeme přítomnost expozice předtím, než je zjištěna přítomnost nemoci nebo jiného studovaného jevu (události). Exponovaní a kontrolní jedinci jsou tedy do studie nabírání ještě před vznikem sledované události, četnost událostí je následně prospektivně sledována v čase (příklad 1, obr. 1). Jako hlavní typ těchto studií zde uvádíme:
- studie kohortové (cohort studies), které na počátku rozdělují osoby na exponované a kontrolní a následně v těchto kohortách sledují výskyt hodnocených událostí v čase (úmrtnost, vznik nemoci, změnu zdravotního stavu); doba sledování musí být nastavena tak, aby se daný typ události podařilo reprezentativně zachytit.
Příklad 1. Výpočet relativního rizika (RR) v prospektivní studii. 
Obr. 1. Schéma sledování asociace jevů v prospektivní studii. 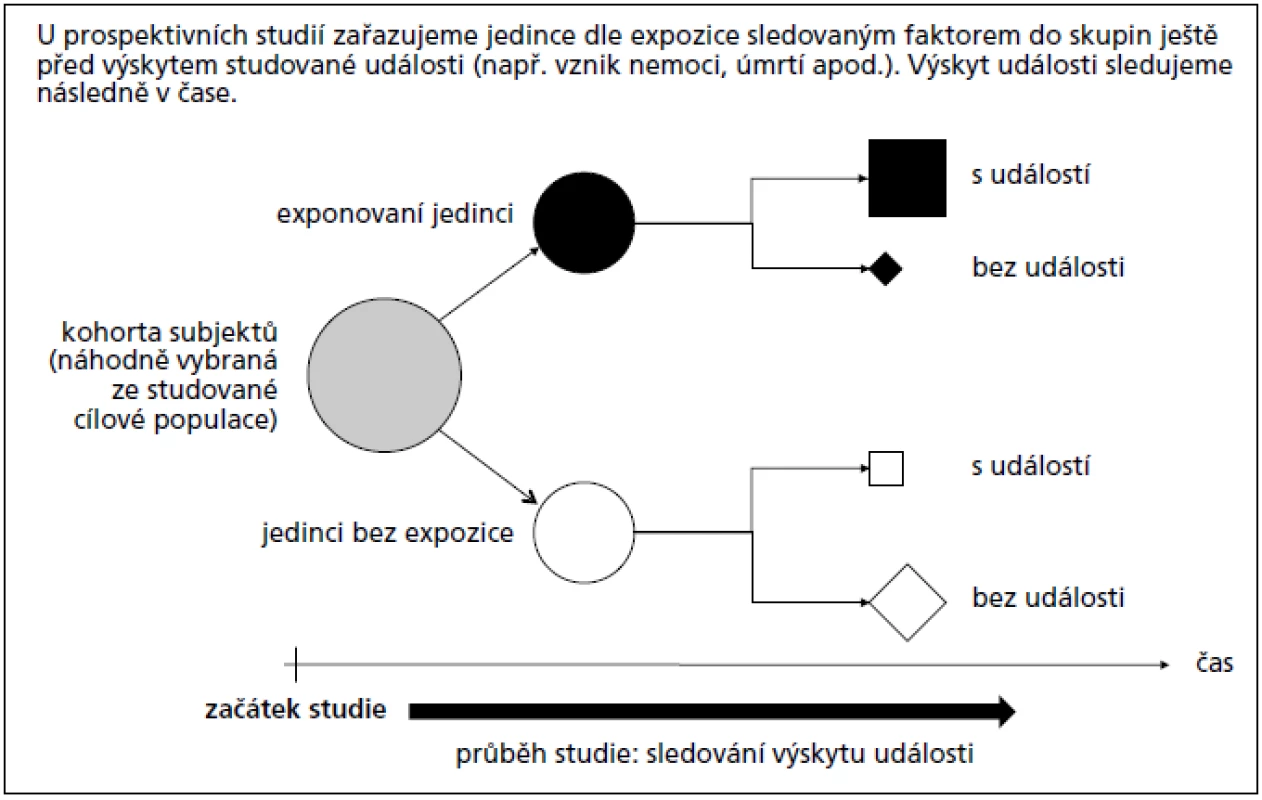
U studií průřezových (cross-sectional studies) studujeme přítomnost expozice daným faktorem a výskyt sledované události ke stejnému časovému okamžiku (periodě), a odhadujeme tak výskyt (prevalenci) obou těchto jevů; z těchto pozorování většinou nelze určit, zda expozice předcházela výskytu sledované události, či naopak.
U retrospektivních studií nejprve vybíráme jedince, u kterých se vyskytla daná nemoc nebo jiná sledovaná událost a následně zpětně zjišťujeme, zda byli, nebo nebyli exponováni studovanému faktoru. Zjištění stavu expozice (jako možné příčiny sledované události) tedy následuje až po zjištění výskytu události. K jedincům se sledovanou událostí pak dle vhodného klíče vybíráme jedince kontrolní, respektive jedince bez sledované události (i u nich následně zjišťujeme stav expozice). Jelikož jsme osoby s událostí a bez ní do studie zařazovali sami a přímo, nemůžeme v takovém experimentu považovat výskyt události za reprezentativní, což má za následek, že tyto studie neumožňují odhadnout její incidenci nebo prevalenci. Typickým příkladem takového experimentálního plánu jsou:
- studie případů a kontrol (case-controls studies), ve kterých vybíráme osoby dle přítomnosti/nepřítomnosti nemoci (události) a zpětně zjišťujeme, zda v minulosti proběhla expozice sledovaným faktorem; cílem je srovnání skupin v přítomnosti nebo i intenzitě expozice a posouzení jejího vlivu, nikoli reprezentativní odhad incidence dané události,
- vyvážené studie případů a kontrol (matched case-control studies), ve kterých při zařazování jedinců dle přítomnosti/nepřítomnosti nemoci (události) dále dbáme na jejich srovnatelnost v určených významných charakteristikách (nejčastěji srovnatelnost v zastoupení pohlaví, ve věkových kategoriích apod.).
Z výše uvedeného popisu hlavních typů studií jednoznačně vyplývá pravidlo pro různé a nezaměnitelné využití poměru šancí a relativního rizika:
- Relativní riziko (RR) můžeme využít pouze u prospektivních a průřezových studií, neboť zkoumané osoby jsou vybírány náhodně, tj. bez ohledu na přítomnost nemoci nebo jiné cílové události (obr. 1). V takovém případě můžeme reprezentativně odhadnout pravděpodobnost výskytu sledované události v exponované a kontrolní skupině a výsledný odhad RR je podílem těchto pravděpodobností (příklad 1). Pozorovaná četnost dané události zde není ovlivněna výběrem jedinců do studie; prospektivní design studie umožňuje reprezentativně hodnotit výskyt jevu v čase, a korektně tak odhadnout příslušnou pravděpodobnost. Tento odhad není možný u retrospektivních studií, které pacienty nabírají přímo podle výskytu události. U retrospektivních studií tedy nelze odhad RR korektně využít.
- Poměr šancí (OR) lze uplatnit u všech výše uvedených typů studií, hlavní význam má však u retrospektivních studií. U těchto studií totiž probíhá náběr jedinců podle výskytu události a teprve zpětně sledujeme přítomnost (vliv) expozice určitým faktorem. Z takto získaného vzorku nemůžeme korektně odhadovat pravděpodobnost výskytu sledované události v populaci, neboť hrozí riziko zkreslení (obr. 2). Nicméně můžeme odhadovat šanci výskytu události ve skupině exponovaných a kontrolních jedinců a tyto šance dávat do poměru; výsledný poměr šancí (OR) tak korektně kvantifikuje vliv hodnocené expozice na danou událost (příklad 2). U prospektivních a průřezových studií lze poměr šancí také počítat, ale vzhledem k použitelnosti a snazší interpretovatelnosti relativního rizika je to spíše výjimkou.
Obr. 2. Schéma sledování asociace jevů v retrospektivní studii. 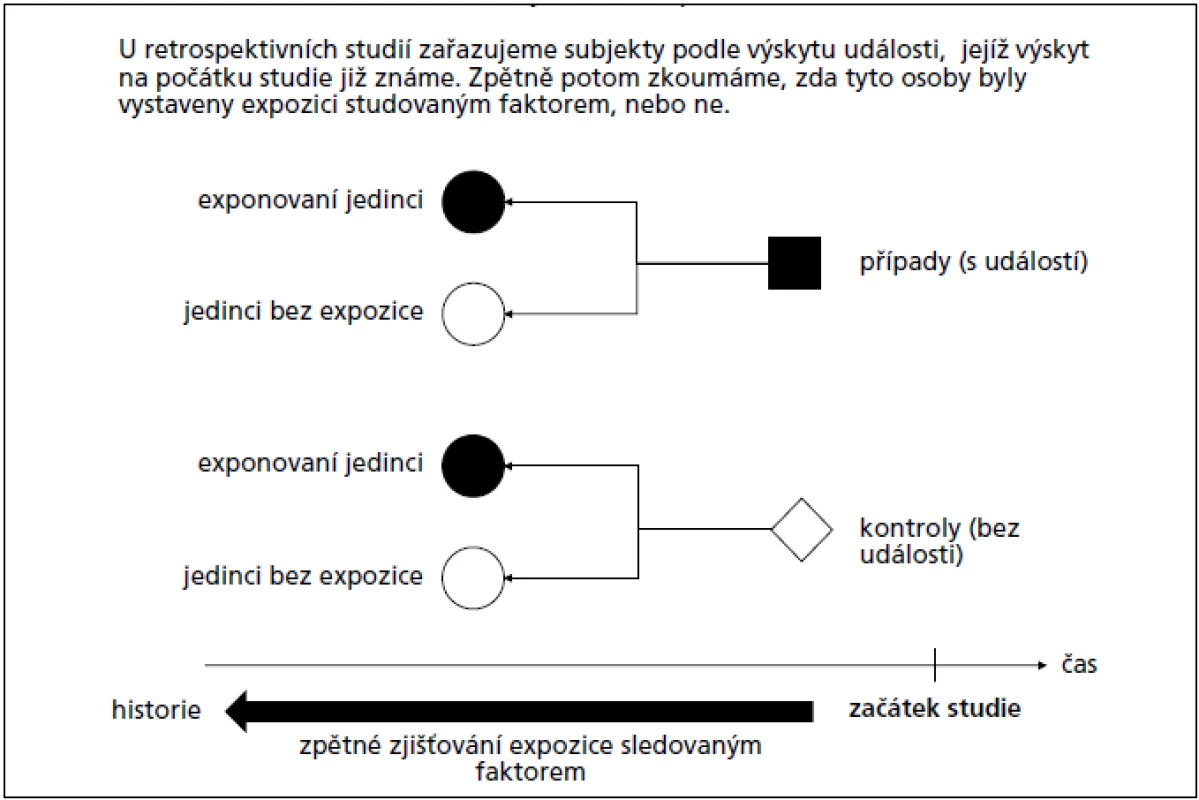
Příklad 2. Výpočet poměru šancí (odds ratio, OR) v retrospektivní studii. 
Pokud při analýze dat dodržíme tato relativně jednoduchá pravidla pro aplikaci OR a RR, je další postup již výpočetně jednoduchý, neboť práce s tabulkami četností není limitována žádnými předpoklady o rozdělení pravděpodobnosti. Příklady 1 a 2 ukazují prakticky využitelné výpočty odhadu OR a RR a nadto doplňují jednoduchý postup, kterým lze přímo z tabulky četností vyhodnotit i interval spolehlivosti těchto odhadů. Pro jednorozměrné hodnocení asociačních tabulek s dostatečným počtem sledovaných jedinců jsou tyto postupy plně dostačující.
Situaci ovšem může zkomplikovat potřeba studovat současně vliv více faktorů na výskyt dané události (nemoci). Rovněž zadání směřující k porovnání odhadů OR nebo RR v různých populacích (kohortách), které se liší četností (pravděpodobností výskytu) dané události nebo hodnotou nějaké významné charakteristiky (např. věku jedinců) vyžaduje zvýšenou opatrnost z důvodu vysokého rizika zkreslení výsledků. K silně zkreslenému závěru můžeme dospět i při hodnocení asociačních tabulek, které obsahují pouze agregovaná data (např. populační) a nikoli individuální data. Přímočarý výpočet poměru šancí nebo relativního rizika může být u takových dat značně zavádějící. V těchto případech se pro odhady OR nebo RR používají komplikovanější postupy, než které uvádíme v tomto díle, např. odhady pomocí regresních modelů. Některé z těchto postupů vysvětlíme v dalších dílech seriálu.
Na závěr této části se krátce vrátíme k uvedené klasifikaci typů studií, kde jsme zdůraznili především časové hledisko. Celý výklad jsme zaměřili na studie observační, neboli neintervenční, které nemají ambici měnit běh událostí a aktivně ovlivňovat sledované subjekty. Zmiňme znovu studie experimentální, které intervenčně ovlivňují chování subjektů a přímo nastavují expozici studovanými faktory. Tyto studie jsou ze své podstaty v naprosté většině prospektivní, tedy nejprve je proveden experimentální zásah a následně jsou zařazené osoby sledovány a hodnoceny v čase. Nejvhodnějším ukazatelem míry asociace mezi expozicí a sledovanou událostí je v tomto případě, stejně jako u prospektivních observačních studií, relativní riziko.
doc. RNDr. Ladislav Dušek, Dr.
Institut biostatistiky a analýz
MU, Brno
e-mail: dusek@cba.muni.cz
Štítky
Detská neurológia Neurochirurgia Neurológia
Článok vyšiel v časopiseČeská a slovenská neurologie a neurochirurgie
Najčítanejšie tento týždeň
2012 Číslo 5- Metamizol jako analgetikum první volby: kdy, pro koho, jak a proč?
- Kombinace metamizol/paracetamol v léčbě pooperační bolesti u zákroků v rámci jednodenní chirurgie
- Neuromultivit v terapii neuropatií, neuritid a neuralgií u dospělých pacientů
- Antidepresivní efekt kombinovaného analgetika tramadolu s paracetamolem
- Srovnání analgetické účinnosti metamizolu s ibuprofenem po extrakci třetí stoličky
-
Všetky články tohto čísla
- Vliv malých dávek vína či jiných alkoholických nápojů na lidské zdraví a délku života
- Emoční paměť – patofyziologie a klinické souvislosti
- Endovaskulární léčba intrakraniálních aneuryzmat – metodika, indikace, komplikace
- Validita a prediktivní hodnota skríningových testů u prediabetické a časné diabetické polyneuropatie
- Komentář k práci Š. Buršové et al
- Incidence a rizikové faktory pooperačního deliria
- Bezpečnost a účinnost intravenózní trombolytické terapie mozkového infarktu u pacientů nad 80 let věku
- Likvorový triplet (tau proteiny a beta-amyloid) v diagnostice Alzheimerovy-Fischerovy nemoci
- Zhoršení kognitivních funkcí a snížení perfuze v kontralaterálním frontálním laloku u pacientů s lézí mozečku
- Baha jako řešení jednostranné hluchoty po operaci vestibulárního schwannomu
- Sekvestrace MBNL1 proteinu mutovaným ZNF9 mRNA v lymfocytech pacientů s myotonickou dystrofií 2. typu
- Lze detekovat intrakraniální venózní reflux z transkondylárního přístupu? Výsledky studie s Fusion Imaging
- Náhrada defektu kalvy u dítěte po úrazu CNS biokompatibilním materiálem na míru – kazuistika
- Motorické stereotypie v dětském věku – kazuistiky
- Léčba spinálních paragangliomů – kazuistiky
- Amyotrofická laterální skleróza v zařízení paliativní hospicové péče – kazuistika
- Idiopatická stenóza akveduktu a porucha vývoje řeči u dětí s neurofibromatosis von Recklinghausen typ 1 – dvě kazuistiky
- Neurologické komplikace spojené s asistovanou reprodukcí – kazuistika
- Webové okénko
-
Analýza dat v neurologii
XXXV. Rozlišujme poměr šancí a relativní riziko -
8. olomoucké neuroimunologické sympozium s mezinárodní účastí
Olomouc, 20.–21. 9. 2012
- Česká a slovenská neurologie a neurochirurgie
- Archív čísel
- Aktuálne číslo
- Informácie o časopise
Najčítanejšie v tomto čísle- Motorické stereotypie v dětském věku – kazuistiky
- Emoční paměť – patofyziologie a klinické souvislosti
- Neurologické komplikace spojené s asistovanou reprodukcí – kazuistika
- Likvorový triplet (tau proteiny a beta-amyloid) v diagnostice Alzheimerovy-Fischerovy nemoci
Prihlásenie#ADS_BOTTOM_SCRIPTS#Zabudnuté hesloZadajte e-mailovú adresu, s ktorou ste vytvárali účet. Budú Vám na ňu zasielané informácie k nastaveniu nového hesla.
- Časopisy



