-
Články
- Časopisy
- Kurzy
- Témy
- Kongresy
- Videa
- Podcasty
Temporomandibulární kloub a jeho 2D a 3D modely
Temporomandibular Point and Its 2D and 3D Models
The aim of study is creating the two dimensional plain modeling of temporomandibular point. Three different pressures and movements are evaluated.
Key words:
dentistry - temporomandibular joint - mathematical modeling
Autori: P. Hliňáková 1; T. Dostálová 1; J. Daněk 2; J. Nedoma 3
Pôsobisko autorov: Dětská stomatologická klinika 2. LF UK a FN Motol, Praha 1; Katedra matematiky, Západočeská univerzita v Plzni 2; Ústav informatiky, Akademie věd ČR, Praha 3
Vyšlo v časopise: Česká stomatologie / Praktické zubní lékařství, ročník 108, 2008, 1, s. 3-7
Kategória: Články
Súhrn
Cílem studie je vytvoření lineárního dvourozměrného matematického zobrazení kloubu při třech typech zatížení a pohybu.
Klíčová slova:
temporomandibulární kloub - matematický modelÚVOD
Dynamické matematické modelování je disciplina, která umožňuje pochopit biomechaniku komplexu anatomického a funkčního pohybu kloubu, v tomto případě temporomandibulárního kloubu [7].
ZÁKLADNÍ ANATOMICKÉ POZNÁMKY
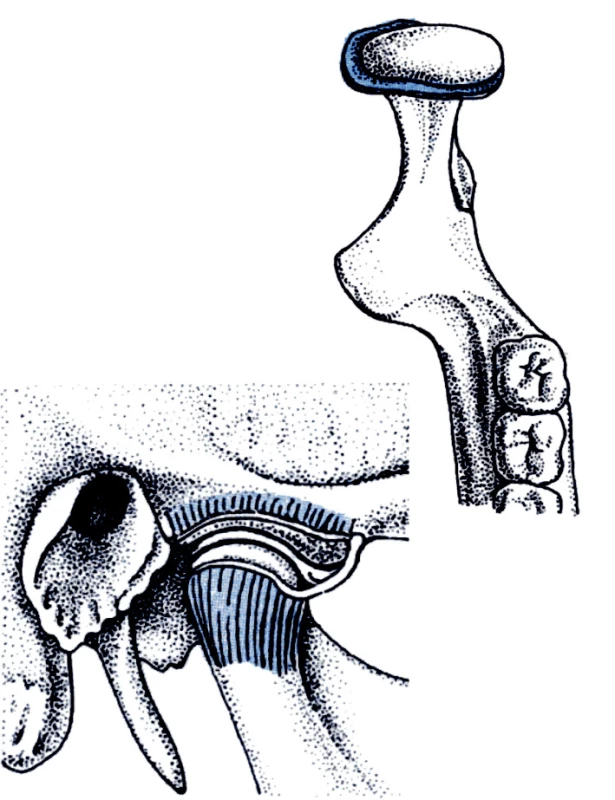
Čelistní kloub je složený kloub zajišťující spojení mezi pohyblivou dolní čelistí a nepohyblivou spánkovou kostí spodiny lebeční. Je to typický bilaterální kloub, ve kterém oba klouby tvoří funkční jednotku, kde jakákoliv změna jedné strany funkčně ovlivňuje kloub strany opačné (obr. 1) [5].
Obr. 1. Temporomandibulární kloub. 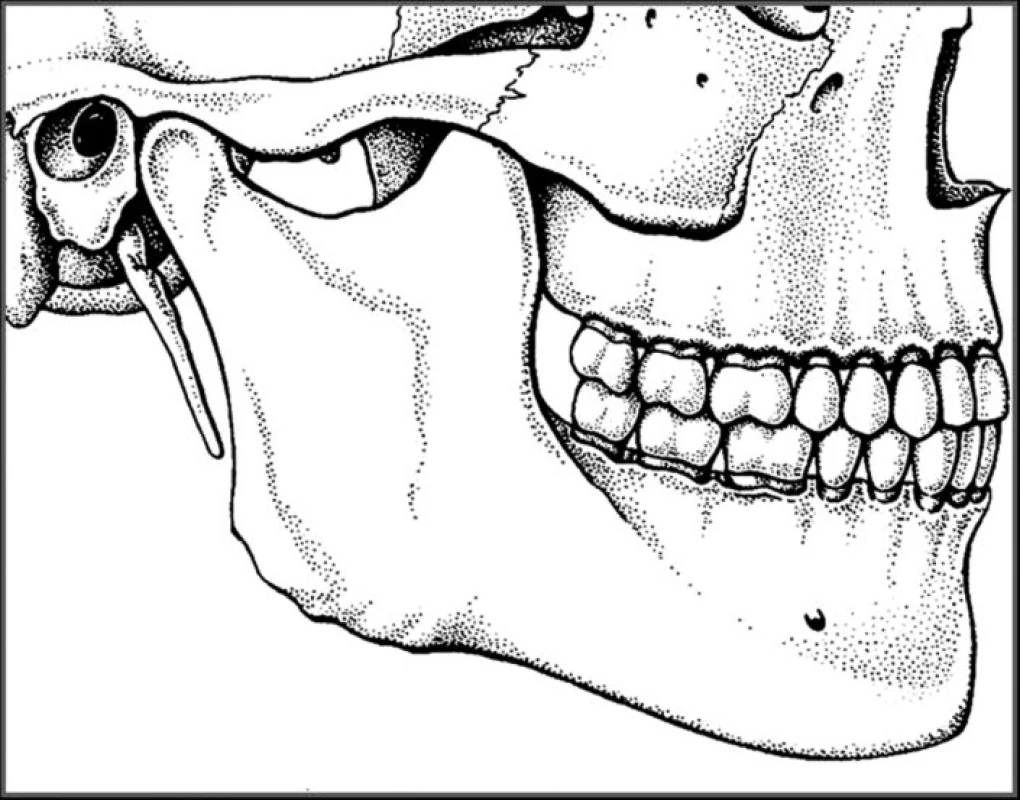
Čelistní kloub (articulatio temporomandibularis) tvoří hlavička, neboli kondyl a čelistní jamka, doplněná vpředu kloubním hrbolkem kosti spánkové. Kondyl má tvar rotačního elipsoidu s podlouhlou osou uloženou horizontálně, tloušťkou 10 mm a šířkou 20 mm (obr. 2). Podélné osy obou kondylů spolu svírají dopředu otevřený úhel 150 -160 stupňů (obr. 3). Kloubní plochy jsou pokryty vazivovou chrupavkou, která nahradila chrupavku hyalinní, jež se nachází ve většině synoviálních kloubů. Vazivová chrupavka má větší odolnost vůči degenerativním změnám a vyšší schopnost regenerace [9].
Obr. 3. Úhel mezi oběma kloubními hlavicemi. 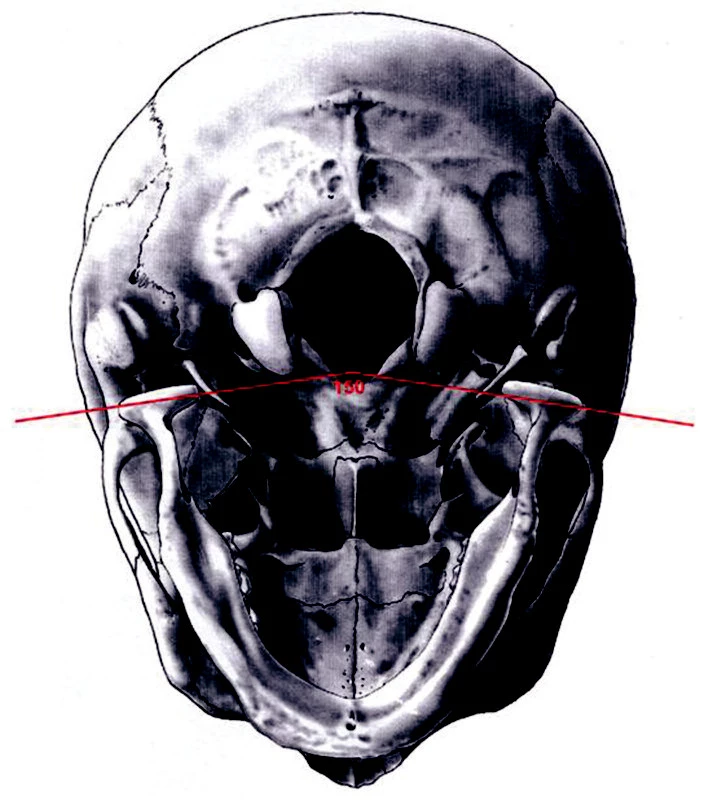
Další specifikou temporomandilárního kloubu je přítomnost artikulační ploténky (discus articularis), která vyrovnává rozdíly v zakřivení styčných ploch kloubu. Má podobu destičky se složitou vnitřní strukturou. Po celém obvodu je zavzata do kloubního pouzdra a tím rozděluje kloubní prostor na dvě zcela oddělené části, a to: horní (diskotemporální) a dolní (diskomandibulární) (obr. 4). Je sedlovitě prohnutá a ve středu tenčí než po obvodu. Kloubní pouzdro tvaru nálevky otevřené nahoru se upíná na okraji hlavičky a po obvodu celé kloubní plochy na spánkové kosti, včetně tuberculum articulare. Je zesíleno vazy na zevní i vnitřní ploše. Během života dochází v čelistním kloubu ke změnám. Při narození a v dětském věku jsou kloubní hrbolky plošky kondylů a jamky oploštělé, což umožňuje rozsáhlejší klouzavé pohyby. Kloubní disk má při narození tvar ploché ploténky, která své charakteristické zakřivení získává během rozvoje kloubních ploch. Definitivní podobu má kolem 20.-25. roku života. Disk zprvu rozděluje kloubní dutinu na dvě části, po 50. roku věku dochází často k perforaci ve střední části disku. To je způsobeno degenerativními změnami, které zapříčiní zeslabení disku, prasknutí či jeho roztržení. Čelistní kloub, podobně jako jiné klouby, se vyznačuje značnou schopností adaptace, ale kloubní disk je strukturou neobsahující cévy, a proto jeho schopnost adaptace je nulová.
Obr. 4. Kloubní disk a kloubní pouzdro. 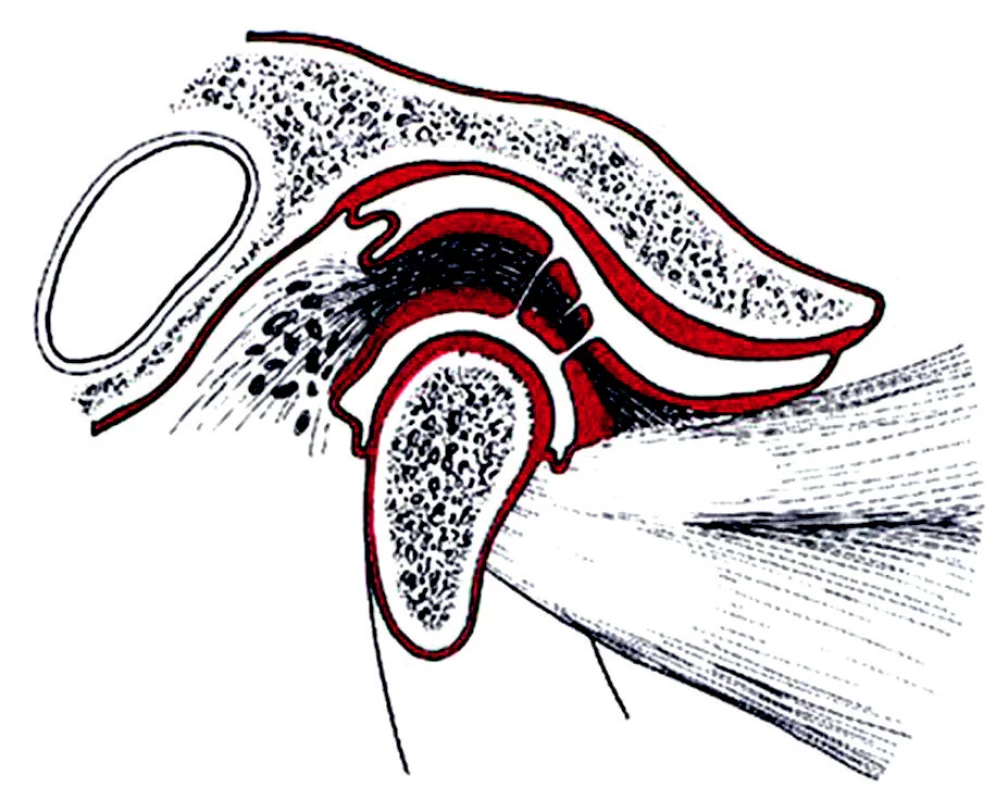
MECHANIKA ČELISTNÍHO KLOUBU
Stavba čelistního kloubu je velmi složitá a umožňuje pohyby a souhyby s druhostranným čelistním kloubem při ukusování, žvýkání a mluvení.
Pohyby čelistního kloubu jsou komplikované a biomechanicky dosud ne zcela objasněné [3].
V zásadě zde dochází ke dvěma typům pohybů:
- pohyb rotační (otáčivý),
- pohyb translační (posuvný).
Při rotačním pohybu je disk stlačován, při translačním se protahuje a zkracuje. Většina pohybů je však kombinovaných. Výsledkem jsou tyto základní pohyby dolní čelisti:
1. Deprese mandibuly (otevírání úst) je prováděna suprahyoidními svaly (m. digastricus, m. mylohyoideus a m. geniohyoideus). Při pootevření úst v první fázi kondyly rotují kolem horizontální osy, v další fázi otvírání úst se kondyly spolu s disky posouvají dopředu až se při maximálním otevření úst dostanou na kloubní hrbolek. Rotační osa se v této fázi pohybu dostává mimo vlastní kloub.
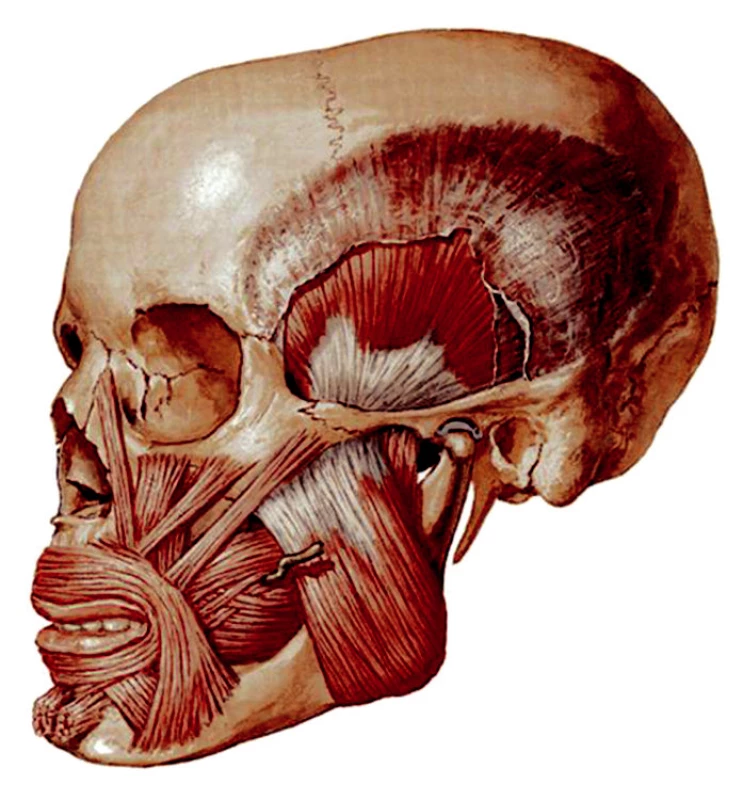
2. Elevace mandibuly – zavírání úst zajišťují žvýkací svaly (m. masseter, m. pterygoideus mediális et lateralis, m. temporalis) (obr. 5). Při tomto pohybu dochází k posunu disku vzad a s ním současně klouže hlavice. Uvolnění m. pterygoideus lateralis poté umožní návrat disku až do kloubní jamky.
3. Protrakce (propulze) mandibuly je posun mandibuly ze základní polohy vpřed. Kondyly se posouvají vpřed a dolů. Tento typ pohybu oboustranně provádějí mm. pterygoidei laterales, spolupodílí se m. masseter a m. pterygoideus medialis.
4. Rektrakce (retropulze) mandibuly je posun mandibuly ze základní polohy vzad, na kterém se podílí zadní snopce m. temporalis, hluboká část m. masseter a také m. digastricus.
Při žvýkání se k výše jmenovaným pohybům přidávají ještě pohyby dolní čelisti do stran, tzv. lateropulze. Jde o posun mandibuly ze základní polohy do strany. Jedná se vlastně o retrakci na jedné straně spojenou s protrakcí na straně druhé. Na pohybech a vedení mandibuly se rozhodující měrou podílejí žvýkací svaly, zatímco temporomandibulární kloub ovlivňuje vedení dolní čelisti jen v extrémních pohybech.
MATEMATICKÉ MODELY TMK
Z hlediska statiky mandibuly jsou důležité tyto základní polohy:
1. Klidová poloha - představuje rovnovážný stav skupin svalů podílejících se na pohybech mandibuly. Je ovlivněna řadou statických a dynamických faktorů, kam řadíme výšku skusu – vzdálenost mezi alveolárními výběžky obou čelistí při skusu, napětí svalů, polohou a držením hlavy, únavou žvýkacích svalů a podobně.
2. Centrální poloha – tuto polohu zaujímá dolní čelist při polknutí sousta.
3. Habituální poloha - mezi čelistmi je navozen habituální stav, do této polohy se mandibula dostává na konci žvýkání nebo i vědomě při maximální interkuspidaci.
Z hlediska dynamiky je čelistní kloub součástí žvýkacího aparátu, jehož funkcí je mastikace, což je akt, který vychází z klidové polohy či habituální polohy a po depresi a následné elevaci spojené s retruzní a laterální exkurzí končí návratem dolní čelisti do polohy maximální okluze. Při žvýkání vytvářejí žvýkací svaly tzv. žvýkací sílu, jejíž velikost může být při maximálním stisku až 4000 N. Tato síla je přenášena z mandibuly na lební bazi kloubní cestou (temporomandibulárním kloubem) a dentoalveolární cestou (přes zuby a alveolární výběžky a dále přes spánkovou kost). Žvýkací sílu přenášejí lebeční kosti (dolní a horní čelist, kost lícní, čelní a spánková), zuby a ozubice, ploténka čelistního kloubu. Ploténka čelistního kloubu přenáší značnou žvýkací sílu a je důležitým faktorem tlumícím absolutní sílu žvýkacího svalstva. Vzhledem k tomu, že ploténka má nepravidelnou tloušťku (uprostřed je tenčí) i rozklad sil je nerovnoměrný [2, 4].
Při sledování anatomické stavby čelistního kloubu a zmapování možných pohybů dolní čelisti, které přímo souvisejí s čelistním kloubem, a s ohledem na skutečnost, že jsou oba klouby spojeny dolní čelistí, a tím i vzájemně ovlivňovány, je velmi obtížné přesně popsat a matematicky definovat procesy, ke kterým v kloubu a jeho okolí dochází, což je nezbytné pro vytvoření dynamických matematických modelů [1, 3, 8].
Modely ozřejmí vztahy mezi strukturou a funkcí kloubů a mají demonstrovat přijatelnou muskuloskeletární mechaniku. Modelování využívá počítačovou tomografii (CT) a nukleární magnetickou rezonanci (MRI), jejich hardwarové a softwarové vybavení s vysokou rozlišovací schopností (volitelnosti rozlišení kontrastu, možnosti provedení série tomogramů a současně provedení celkového radiogramu apod.).
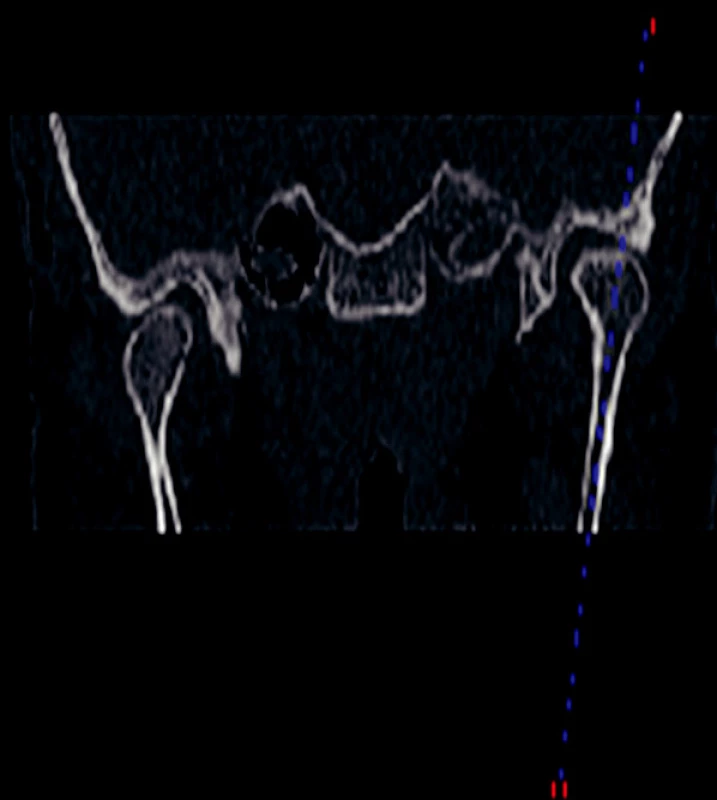
V této studii byly pro temporomandibulární kloub vytvořeny 3 rovinné modely, které charakterizují procesy, ke kterým v čelistním kloubu dochází. Snímky z MRI ukazují boční a přední pohled a pro usnadnění orientace je zde naznačena úsečka (respektive její průměty). Uvažovaný řez obsahuje tuto úsečku a byl nalezen otáčením roviny řezu okolo této úsečky (obr. 6, obr. 7, obr. 8). Jsou pro všechny modely identické.
Obr. 6. MRI snímek TMK předozadní. 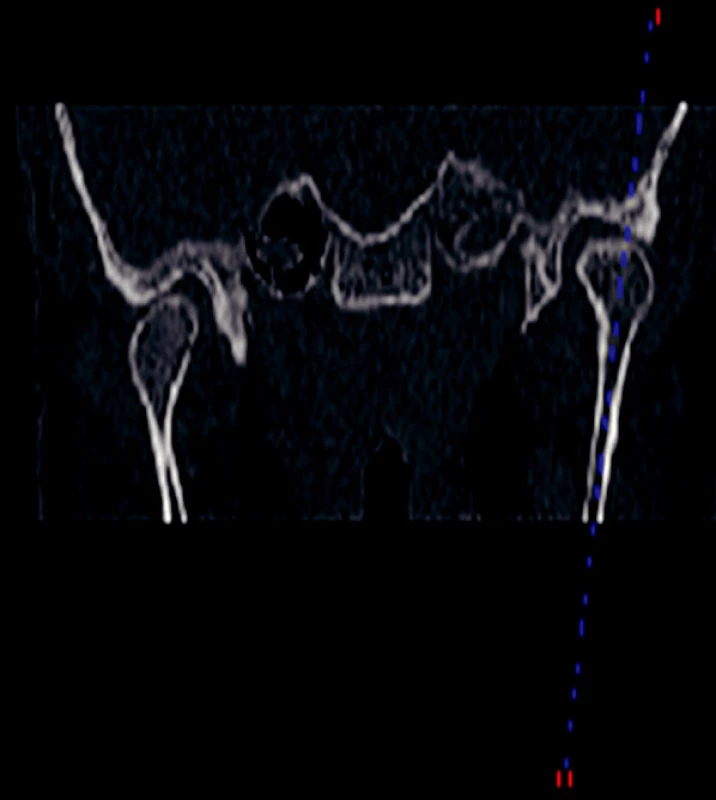
Obr. 8. MRI snímek TMK uvažovaný řez. 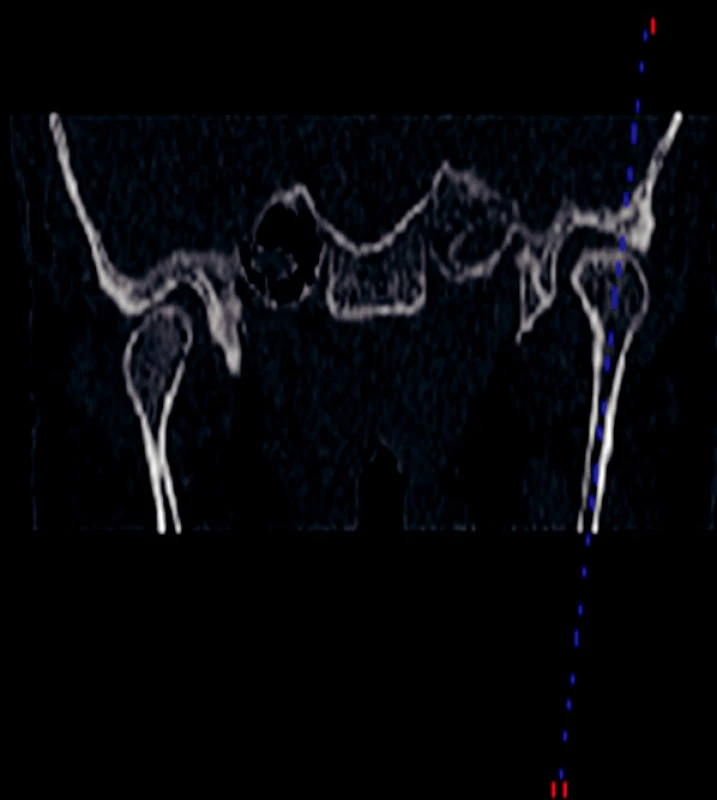
Na základě obrazu počítačové tomografie (CT) a nukleární magnetické rezonance (MRI) byl vytvořen dvou-dimenzionální matematický model, který by měl pomoci charakterizovat procesy, ke kterým v čelistním kloubu dochází. Užitý matematický model umožňuje analyzovat mechanická a biomechanická hodnocení kloubního spojení čelistního kloubu v souvislosti s možností aplikace náhrady čelistního kloubu jeho umělou totální náhradou. Má-li totální náhrada čelistního kloubu spolehlivě plnit svoji funkci a plně zajistit jeho dlouhodobou pohybovou aktivitu, potom jeho konstrukce i následná klinická aplikace musí respektovat biomechanické poměry i při maximálním zatěžování čelistního kloubu.
Přirozený kloub představuje rovnovážný systém, kde tvar odpovídá funkci. Porušení této rovnováhy vede k mechanickému selhání čelistního kloubu, k jeho destrukci. Podobně je tomu i v případě jeho umělé náhrady. Proto cílem matematického modelování funkce přirozeného i umělého čelistního kloubu je i předcházení následků porušení této rovnováhy, resp. následné destrukci přirozeného i umělého kloubu.
Čelistní kloub je namáhán jak silou tahovou, tak silou tlakovou. Při tahové síle jsou kontaktní plochy od sebe odtahovány, při tlakové síle jsou k sobě přitlačovány. Působení tahové síly je v podstatě zachycováno vazy a kloub slouží jako pohyblivé spojení umožňující relativní pohyby spojených částí skeletu čelistního kloubu, avšak s jistým omezením, matematicky toto omezení modelujeme jako „gap“. Při tlakových silách jsou kontaktní plochy k sobě přitlačovány, takže k relativním pohybům spojených částí skeletu čelistního kloubu dochází převážně v podmínkách těsného kontaktu kluzných kloubních ploch pod tlakem. Kloub se v tomto případě chová jako pružné tlakové spojení, při kterém silové působení je navíc „vícesměrné“ podle okamžité funkce čelistního kloubu.
V důsledku namáhání čelistního kloubu značnými silami dochází v oblasti čelistního kloubu ke koncentraci tlakového napětí na poměrně malou plochu kloubu. Díky elasticitě chrupavčitého krytu kontaktních ploch se tato kontaktní plocha zvětšuje, čímž se zatížení přenáší na větší plochu. Nezastupitelnou funkci má i synoviální tekutina, která vedle vyživovací funkce dodává pružnost chrupavčitým krytům kloubní plochy a navíc je schopna svými viskózně elastickými vlastnostmi zachytit a přenášet určitou hodnotu tlakového napětí.
Na kontaktních plochách mezi jednotlivými komponentami čelistního kloubu a jeho umělými náhradami dochází k postupnému opotřebení, navíc na kontaktních plochách přirozených a umělých čelistních kloubů působí tření. Jeho velikost je dána stavem kontaktních kloubních ploch. Tření ve smyslu Coulombově závisí na normálové složce působící síly, se zvětšením přítlačné, tj. normálové síly, kde se zvětšuje tření i opotřebení kontaktních ploch. Matematický model čelistního kloubu musí být schopen popsat všechny tyto skutečnosti a musí umožnit také analyzovat poměry na kontaktu mezi hlavicí čelistního kloubu a kloubní jamkou-acetabulem.
Matematická simulace funkce přirozeného i umělého čelistního kloubu bude založena na matematické teorii kontaktních úloh a metodě konečných prvků. Na této teorii založený matematický model dovoluje studovat napěťové a silové poměry na kontaktních plochách, velikost deformace kontaktních ploch a přenos zatěžovacích sil, přenášených z hlavice čelistního kloubu na kloubní jamku a její okolí. Je však třeba si uvědomit, že matematický model je pouze hrubá aproximace skutečnosti. Řadu funkcí kloubního systému v matematickém modelu modelujeme okrajovými podmínkami, jejichž volba závisí na naší intuici a odborné zkušenosti s matematickým modelováním biologických a biomechanických systémů. Matematická analýza teorie kontaktních úloh ukazuje, jak závisí řešení matematické úlohy na okrajových podmínkách, tedy jak stabilní je řešení v závislosti na malých změnách v zadaných datech okrajových podmínek a působících sil.
Matematický model - užitá data:
kost: Youngův modul pružnosti E= .71x1010 Pa, Poissonova konstanta v=0,25,
chrupavka: Youngův modul pružnosti E=4.92x108 Pa, Poissonova konstanta v=0,1.
MATEMATICKÉ MODELOVÁNÍ POHYBŮ TMK
Model 1 – Pohyb je omezen na rozsah 1 mm ve vodorovném a svislém směru. (obr. 9a). Maximální deformace je v oblasti hlavičky a jamky kloubní, silně zatížen je i disk (obr. 9b). Hlavní zátěž probíhá ve vertikálním směru s maximem v proc. coronoideus (obr. 9c). Hlavní tlaková zóna prochází hlavičkou a jamkou kloubní, částečně i svalovým výběžkem, tah se přenáši do incisura mandibulae (obr. 9d).
Obr. 9. Série obrázků pro model č. 1 - a, b, c, d - zleva doprava. 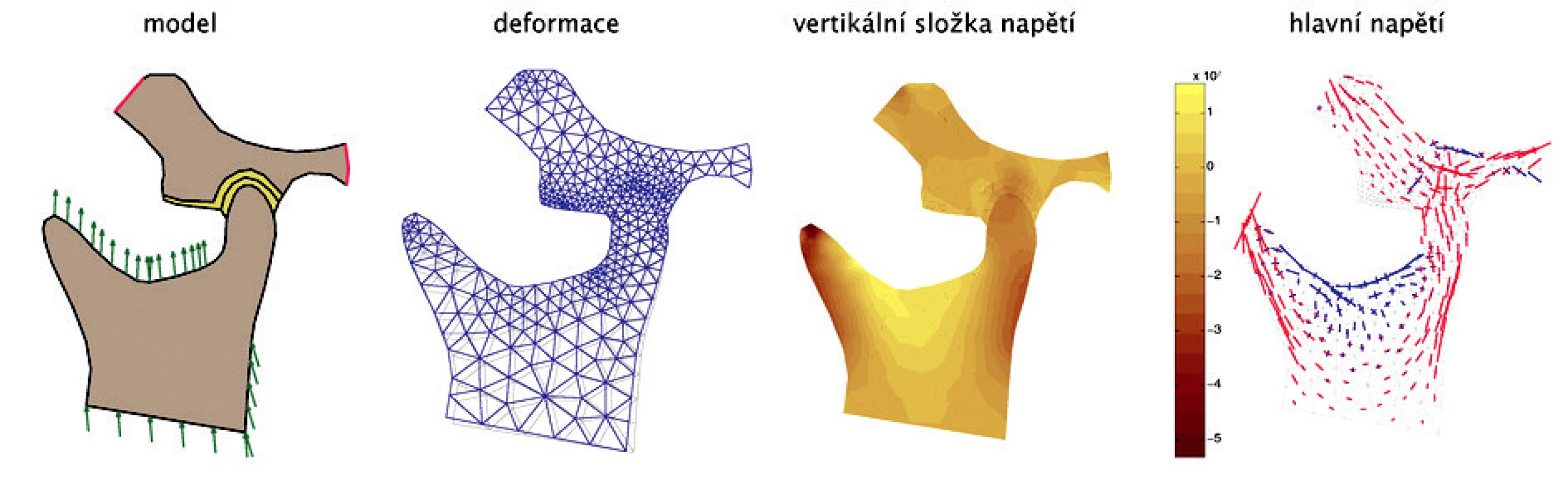
Model 2 - Na schematickém obrázku je v modelu modrou úsečkou naznačena omezená možnost pohybu. Pohyb probíhá v tomto směru (obr. 10a). Hlavní deformační zóna se centralizuje v oblasti kloubní jamky a disku (obr. 10b). Deformace se objevuje na ventrální stěně kloubního výběžku (obr. 10c). Největší tlak v tomto případě prochází kloubní hlavičkou a jamkou, složka tahu se téměř nerozvíjí (obr. 10d).
Obr. 10. Série obrázků pro model č. 2 - a, b, c, d - zleva doprava. 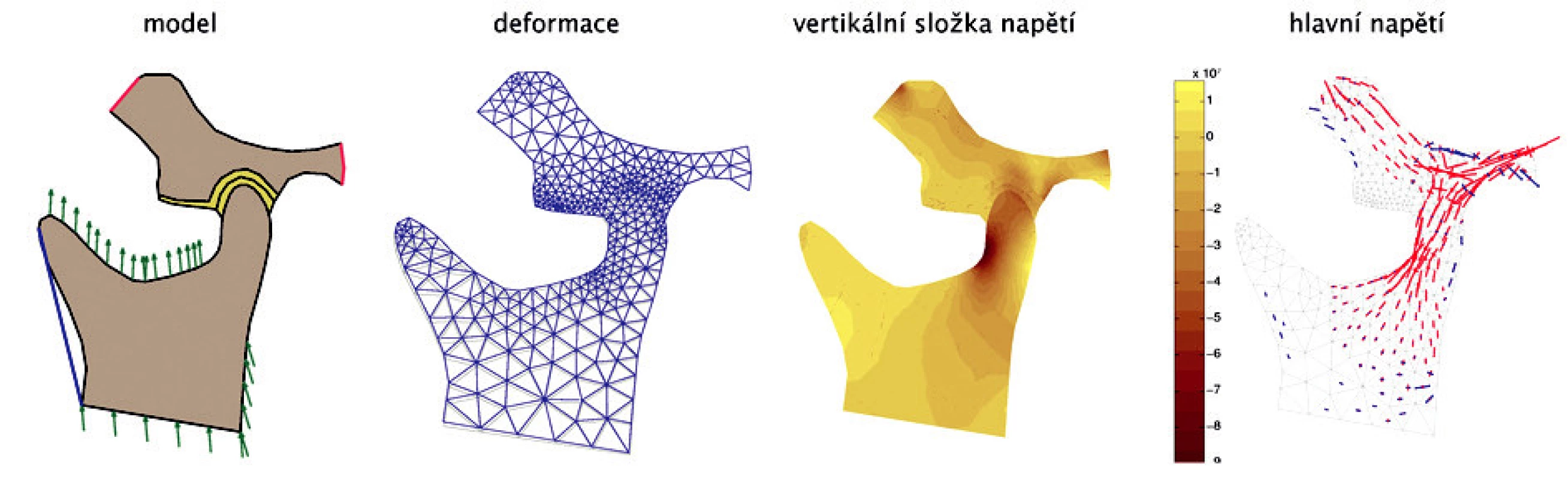
Model 3 - Pohyb simuluje klasické otevírání, zavírání i lateropulze v rozsahu 1 mm (obr. 11a). V tomto modelu je předepsán posun v červeně označeném bodě o velikosti [-1 mm, + 1 mm]. Výsledek nejvíce odpovídá anatomickým znalostem, které o kloubu máme, a to: největší tlakové zatížení kloubní hlavice a části větve (obr. 11b, c), zejména v distální části a tahovému zatížení je vystaven svalový výběžek a incizura (obr. 11d).
Obr. 11. Série obrázků pro model č. 3 - a, b, c, d - zleva doprava. 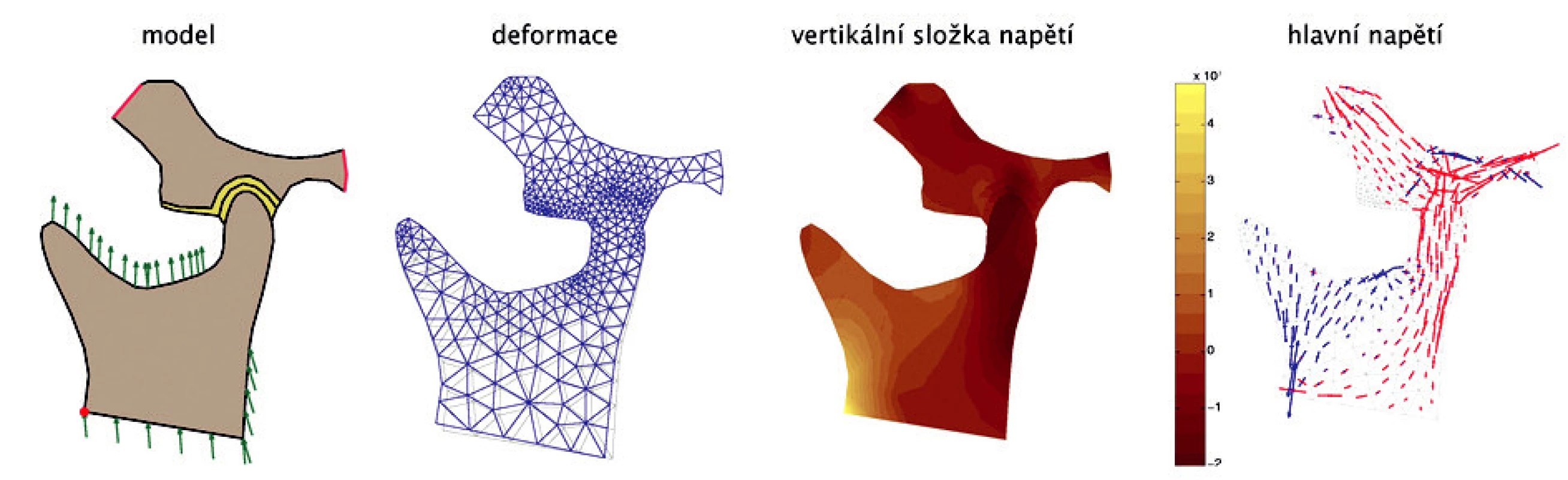
ZÁVĚRY
Po prozkoumání všech tří typů modelů, jejich vzájemného porovnání a konfrontací se stavbou a funkcí čelistního kloubu, docházíme k závěru, že informace, které jsou o čelistním kloubu známy, nejvíce korespondují s modelem č. 3.
Studie vznikla za podpory Výzkumného záměru FN Motol 6307 VZ 00064203.
MUDr. Petra Hliňáková
Dětská stomatologická klinika 2. LF UK a FNM
V Úvalu 84
150 06 Praha 5
Zdroje
1. Fričová, M., Horák, Z., Jirman, R., Konvičková, S.: Modelling of the temporomandibular joint and assessment of the temporomandibular joint disc movement. Journal of Biomechanics, 39, Supplement 1, 2006, s. S493.
2. Hesle F.: The mechanics of the chewing movements of the human jaw. The Journal of Prosthetic Dentistry, 4, 1954, s. 175-178.
3. Koolstra, J. H., van Eijden, T. M. G. J.: The jaw open-close movements predicted by biomechanical modelling. Journal of Biomechanics, 30, 1997, s. 943-950.
4. Koolstra, J. H., van Eijden, T. M. G. J.: Three-dimensional dynamical capabilities of the human masticatory muscles. Journal of Biomechanics, 32, 1999, s.145-152.
5. Okeson, J. P.: Management of temporomandibular disorders and Occlusion. Elsevier Health Sciences, 2007, s. 640.
6. Peck C. C., Langenbach G. E. J. , Hanbam A. G.: Dynamic simulation of muscle and articular properties during human wide jaw mening. Archives of Oral Biology, 45, 2000, s. 963-982.
7. Peck, CH. C., Hanbam, A. G.: Human jaw and muscle modelling. Archives of Oral Biology, 52, 2007, s. 300-304.
8. Trainor, P. G. S., McLachlan, K. R., McCall, W. D.: Modelling of forces in the human masticatory system with optimization of the angulations of the joint loads. Journal of Biomechanics, 28, 1995, s. 829-843.
9. Zarb, G., Carlsson, G. E., Sessle, B. J., Mohl, N. D.: Temporomandibular joint and masticatory muscle disorders. Journal of Oral and Maxillofacial Surgery, 54, 1996, s. 378.
Štítky
Chirurgia maxilofaciálna Ortodoncia Stomatológia
Článok vyšiel v časopiseČeská stomatologie / Praktické zubní lékařství
Najčítanejšie tento týždeň
2008 Číslo 1
-
Všetky články tohto čísla
- Příspěvek ke studiu chrupu brněnských obyvatel v druhé polovině 18. a v 19. století
- Volné radikály a antioxidanty (Souborný referát)
- K životnímu jubileu doc. MUDr. Pavla Hanka, CSc.
- Temporomandibulární kloub a jeho 2D a 3D modely
- Blokáda nervus alveolaris inferior u 284 pacientů se semiretinovanými a retinovanými dolními zuby moudrosti: Naše zkušenosti
- Oprava
- Stomatologické ošetření dětských pacientů v celkové anestezii
- Orální mukositida jako vedlejší účinek myeloablativní chemoterapie u hematoonkologických pacientů
- Česká stomatologie / Praktické zubní lékařství
- Archív čísel
- Aktuálne číslo
- Informácie o časopise
Najčítanejšie v tomto čísle- Temporomandibulární kloub a jeho 2D a 3D modely
- Stomatologické ošetření dětských pacientů v celkové anestezii
- Blokáda nervus alveolaris inferior u 284 pacientů se semiretinovanými a retinovanými dolními zuby moudrosti: Naše zkušenosti
- Orální mukositida jako vedlejší účinek myeloablativní chemoterapie u hematoonkologických pacientů
Prihlásenie#ADS_BOTTOM_SCRIPTS#Zabudnuté hesloZadajte e-mailovú adresu, s ktorou ste vytvárali účet. Budú Vám na ňu zasielané informácie k nastaveniu nového hesla.
- Časopisy