-
Články
- Časopisy
- Kurzy
- Témy
- Kongresy
- Videa
- Podcasty
Optimalizace rekonstrukčních parametrů pro SPECT a SPECT/CT
Optimization of reconstruction parameters for SPECT and SPECT/CT
Purpose:
This work presents results of an optimization of reconstruction parameters, namely number of iterations and number of subsets in OSEM algorithm.Materials and methods:
The optimization was based on contrast and signal to noise ratio measurements on NEMA Body Phantom tomographic reconstructions. Four sets of SPECT projections data were acquired using two different activities at two cameras. Over 500 recontructions using various corrections and resolution recovery algorithm (RR) were realized to scan the parametric space to find the optimal configuration.Results and conclusion:
In the contex of computation time and software instability the best combinations were found as 4 iterations and 10 subsets without using RR and 5 iterations and 10 subsets with RR in matrix 128 x 128, 3 iterations and 12 subsets without RR and 4 iterations and 12 subset with RR in matrix 256 x 256.Key Words:
SPECT, optimization, tomographic reconstruction, image quality
Autoři: Pavel Karhan; Jaroslav Ptáček; Petr Fiala
Působiště autorů: Oddělení lékařské fyziky a radiační ochrany, FN Olomouc a LF Univerzity Palackého
Vyšlo v časopise: NuklMed 2015;4:66-72
Kategorie: Původní práce
Souhrn
Úvod:
Tato práce prezentuje výsledky optimalizace rekonstrukčních parametrů, konkrétně počet iterací a počet subsetů OSEM algoritmu.Materiál a metody:
Optimalizace byla založena na měření kontrastu a poměru signálu k šumu na tomografických rekonstrukcích NEMA Body Fantomu. Byla provedena akvizice čtyř sad projekčních dat se dvěma různými objemovými aktivitami na dvou různých kamerách. Pro nalezení optimálních hodnot byl proskenován parametrický prostor s použitím více než 500 rekonstrukcí s různými korekcemi a resolution recovery algoritmem (RR).Výsledky a závěr:
S přihlédnutím k výpočetnímu času a opakované nestabilitě software byly jako nejlepší kombinace vyhodnoceny 4 iterace a 10 subsetů bez RR a 5 iterací a 10 subsetů s RR v matici 128 x 128, 3 iterace a 12 subsetů bez RR a 4 iterace a 12 subsetů s RR v matici 256 x 256.Klíčová slova:
SPECT, optimalizace, tomografická rekonstrukce, kvalita zobrazeníÚvod
V listopadu 2014 zakoupila Fakultní nemocnice Olomouc dvě nové SPECT kamery řady Discovery od výrobce GE Medical Healthcare. Pro zajištění kvality tomografických vyšetření byla v rámci předávací zkoušky provedena optimalizace rekonstrukčních parametrů, protože doporučení výrobce se výrazně liší od praxe uplatňované na předchozích kamerách. Doporučení SÚJB 1 ani NEMA 2 se bohužel tomuto tématu nevěnují, proto jsme byli nuceni nalézt vlastní postup. Měření byla provedena na NEMA IEC Body Fantomu 3 a data rekonstruována na dodané vyhodnocovací stanici se software Xeleris 3.1 4 od GE Medical Healthcare.
Metoda
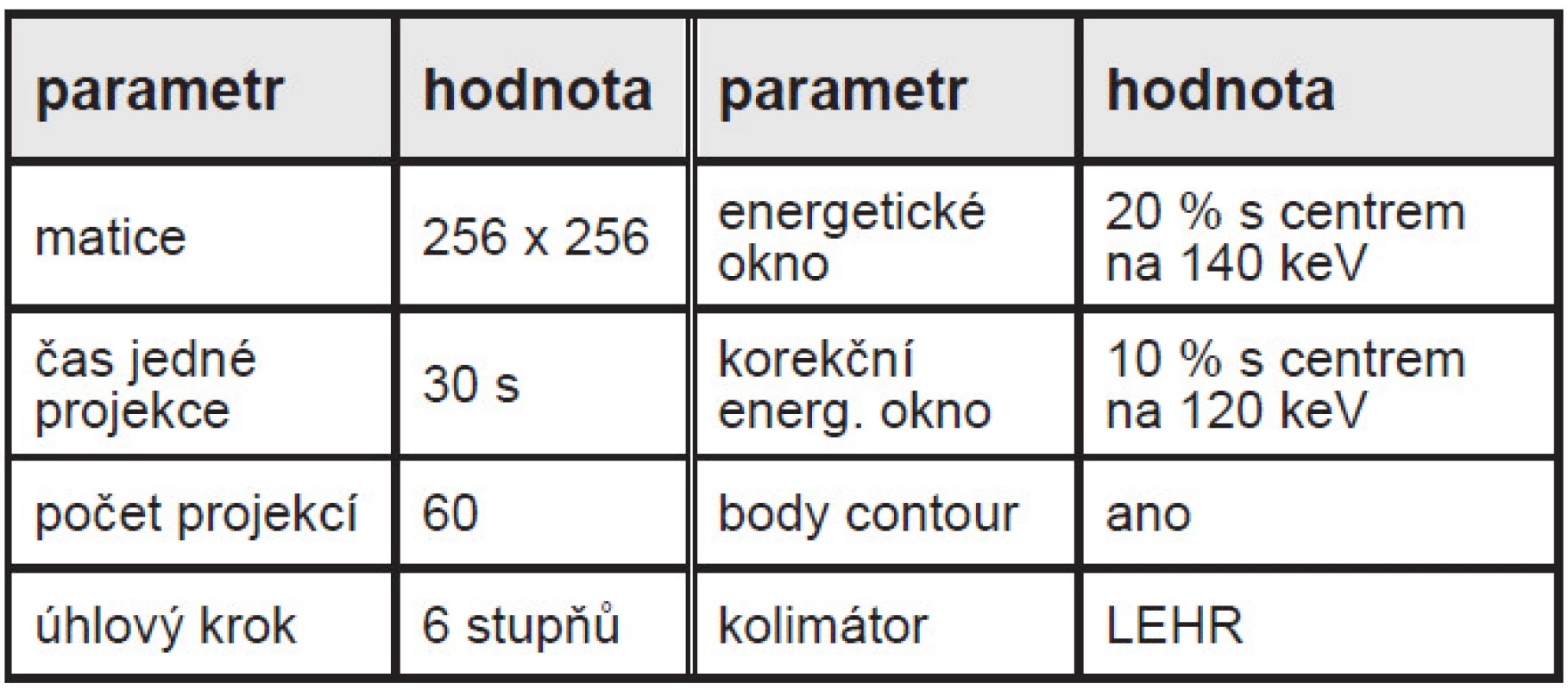
Na každé kameře byla provedena celkem dvě měření s Body Fantomem. Při prvním měření byl aplikován roztok 99mTc o objemové aktivitě 37,3 kBq/ml do těla fantomu a 332,7 kBq/ml do plnitelných lézí, což odpovídá kontrastu mezi lézemi a tělem 7,9 (vysoký kontrast – HC). Pro takto naplněný fantom byl proveden SPECT na přístroji GE Discovery 670 (D670) a následně na přístroji GE Discovery 630 (D630). Pro druhé měření byla do těla fantomu přidána aktivita, čímž objemová aktivita v těle fantomu vzrostla na 68,5 kBq/ml a objemová aktivita v lézi v důsledku radioaktivní přeměny činila 300,6 kBq/ml, což odpovídá hodnotě kontrastu 3,4 (nízký kontrast – LC). Opět byla provedena SPECT měření na obou kamerách v opačném pořadí. Akviziční parametry odpovídaly klinické praxi a jsou uvedeny v tabulce 1. Z časových důvodů nebylo možné provést měření v maticích 256 x 256 i 128 x 128, proto byla provedena akvizice pouze v matici 256 x 256 a pro účely optimalizace pro matici 128 x 128 byla data z větší matice softwarově upravena do menší matice sečtením čtyř sousedních pixelů.
Projekce byly následně rekonstruovány s různými rekonstrukčními parametry algoritmem OSEM. Software umožňuje aplikovat korekce na zeslabení (AC), na rozptyl (SC) a resolution recovery algoritmus (RR). U přístroje Discovery 670, kde je k dispozici CT, byla korekce na zeslabení provedena z CT, u přístroje Discovery 630 byla využita Changova metoda s nastavením dle doporučení výrobce: práh 5 a koeficient útlumu 0,11. Pro analýzu byly provedeny rekonstrukce ve vybraných, v praxi užívaných kombinacích: zcela bez korekce (NC), korekce na zeslabení (AC), korekce na zeslabení s resolution recovery algroitmem (ACRR), korekce na zeslabení a rozptyl (ACSC) a korekce na zeslabení i rozptyl s použitím resolution recovery algoritmu (ACSCRR).
Pro hledání optimálních parametrů byl počítán kontrast 5
a poměr signál-šum 6
Hodnoty signálu S byly určeny jako průměry počtu impulsů v jednotlivých voxelech pro jednotlivé koule Body Fantomu o velikostech 10 mm, 13 mm, 17 mm, 22 mm, 28 mm, 37 mm a pozadí B bylo určeno z těla fantomu jako průměrný počet impulsů v krychlové oblasti v okolí horkých lézí. Léze byly nalezeny neighbor-growing algoritmem s prahem 6
na obrazech vyhlazených Gaussovým filtrem s pološířkou 2 voxely a analýza byla prováděna vždy na nevyhlazených obrazech.
Další parametry, které byly sledovány, ale numericky nezasáhly do optimalizace, jsou recovery koeficient (RC)
a prostorové rozlišení.
Pro optimalizaci jsme zavedli relativní odchylku od změřeného maxima
pro každou veličinu v = {kontrast, SNR} a každou lézi l při rekonstrukčních parametrech p. Takto definovaná veličina je snadno interpretovatelná a leží vždy v rozsahu <0;1>, díky čemuž je možné ji snadno vzájemně porovnávat. Za optimalizační míru byl zvolen vážený součet
takže optimální nastavení parametrů odpovídá minimu veličiny Rp. Váha wv udává míru důležitosti SNR nebo kontrastu pro optimalizaci a volbou váhy wl je možné klást důraz na schopnost detekovat léze určité velikosti.
Rekonstrukce byly provedeny metodou OSEM se 4 iteracemi v kombinaci s 6, 10, 12, 15 a 20 subsety, a pro 10 subsetů v kombinaci s 2, 3, 4, 6, 8 a 10 iteracemi. Po předběžné analýze byly provedeny ještě další rekonstrukce všech možných kombinací počtu iterací a subsetů tak, aby jejich součin ležel v oblasti nalezeného optima. Ze změřených tvarů RC křivky bylo určeno i prostorové rozlišení.
Výsledky
Výsledky předběžné analýzy pro matici 128 x 128 a korekce NC, AC, ACSC jsou vykresleny na Obr. 1, pro korekce ACRR a ACSCRR na Obr. 3. Výsledky detailní analýzy v oblasti minima Rp jsou vykresleny na Obr. 2 a Obr. 4. Výsledky v matici 256 x 256 nejsou kvůli stručnosti uvedeny, protože mají shodné funkční průběhy s tím rozdílem, že při některých kombinacích počtu iterací a subsetů software Xeleris 3.1 nedokončí výpočet a hroutí se, a proto musely být z optimalizace vyřazeny. Závislost kontrastu a SNR na počtu efektivních iterací pro klinicky nejvíce využívané korekce (AC a ACRR) jsou pak na Obr. 5 a Obr. 6. Pro ilustraci, jak bylo určeno prostorové rozlišení, jsou na Obr. 7 uvedeny výsledky z měření na GE Discovery 630 s vysokým kontrastem.
Obr. 1. Optimalizační míra R<sub>p</sub> v závislosti na počtu efektivních iterací pro vysoký (HC) a nízký (LC) kontrast z měření na kamerách GE Discovery 670 (D670) a GE Discovery 630 (D630) pro různé korekce při rekonstrukcích: bez korekce (NC), korekce na zeslabení (AC) a korekce na rozptyl (SC). 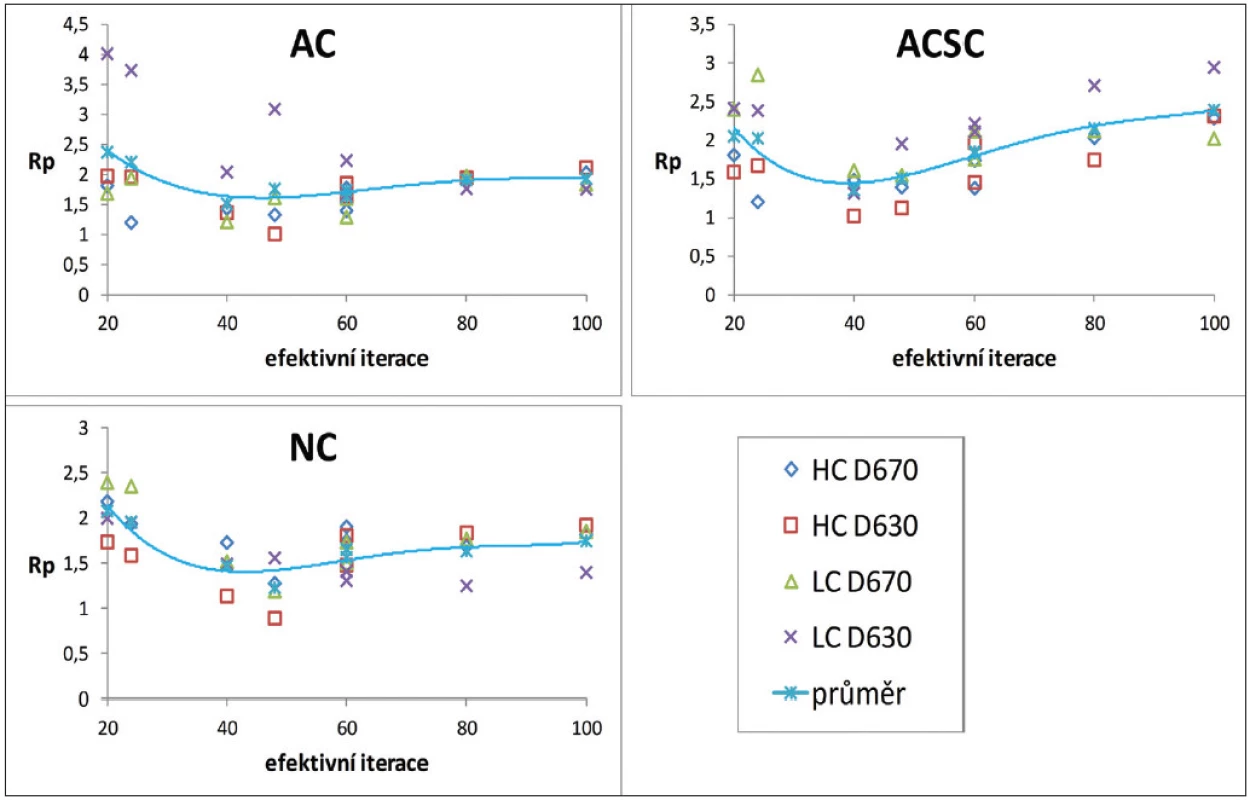
Obr. 2. Optimalizační míra R<sub>p</sub> v závislosti na kombinaci počtu iterací a subsetů v oblasti minima pro vysoký (HC) a nízký (LC) kontrast z měření na kamerách GE Discovery 670 (D670) a GE Discovery 630 (D630) pro různé korekce při rekonstrukcích: bez korekce (NC), korekce na zeslabení (AC) a korekce na rozptyl (SC). 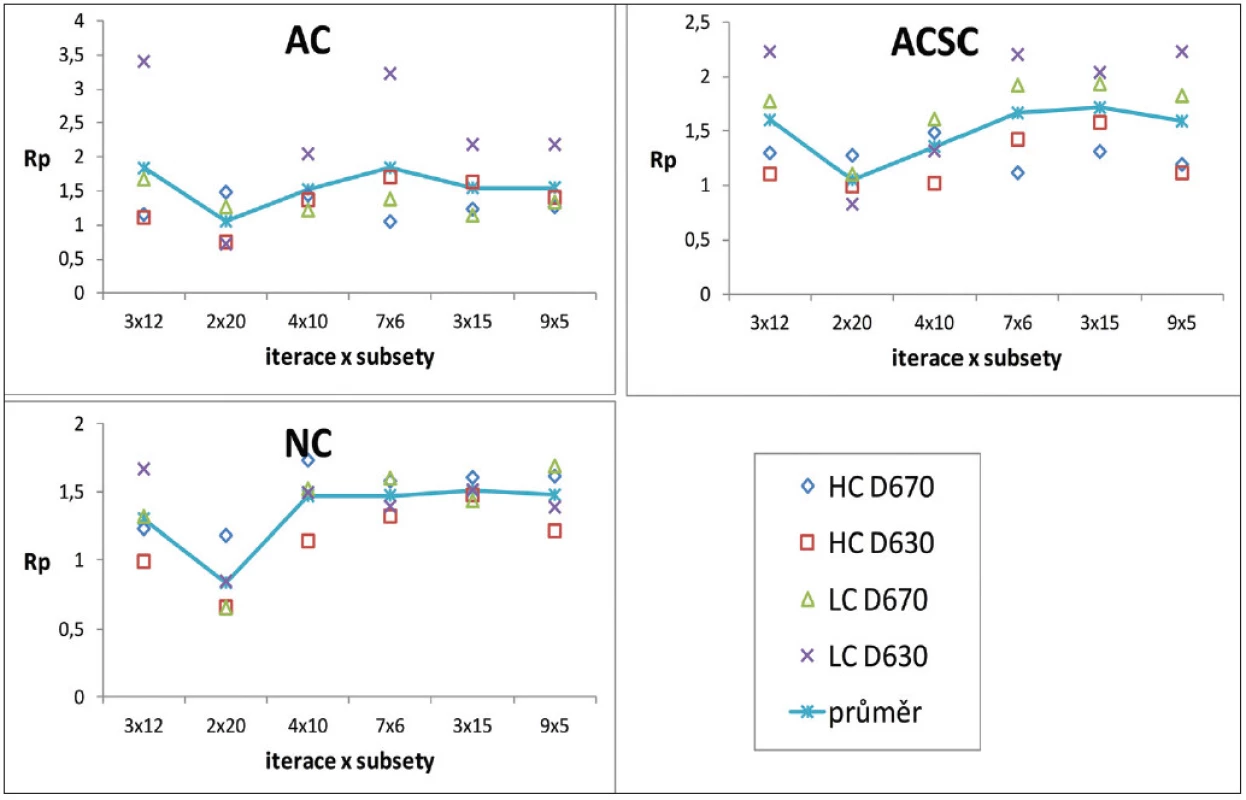
Obr. 3. Optimalizační míra R<sub>p</sub> v závislosti na počtu efektivních iterací pro vysoký (HC) a nízký (LC) kontrast z měření na kamerách GE Discovery 670 (D670) a GE Discovery 630 (D630) pro resolution recovery algoritmus (RR) a různé korekce při rekonstrukcích: korekce na zeslabení (AC) a korekce na rozptyl (SC). 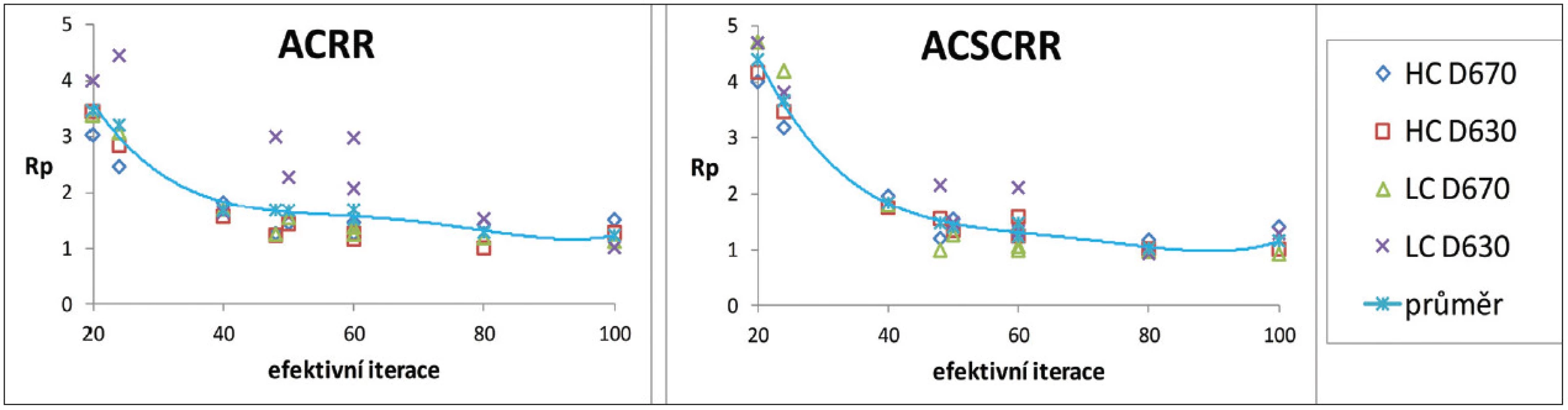
Obr. 4. Optimalizační míra R<sub>p</sub> v závislosti na kombinaci počtu iterací a subsetů v oblasti minima pro vysoký (HC) a nízký (LC) kontrast z měření na kamerách GE Discovery 670 (D670) a GE Discovery 630 (D630) pro resolution recovery algoritmus (RR) a různé korekce při rekonstrukcích: korekce na zeslabení (AC) a korekce na rozptyl (SC). 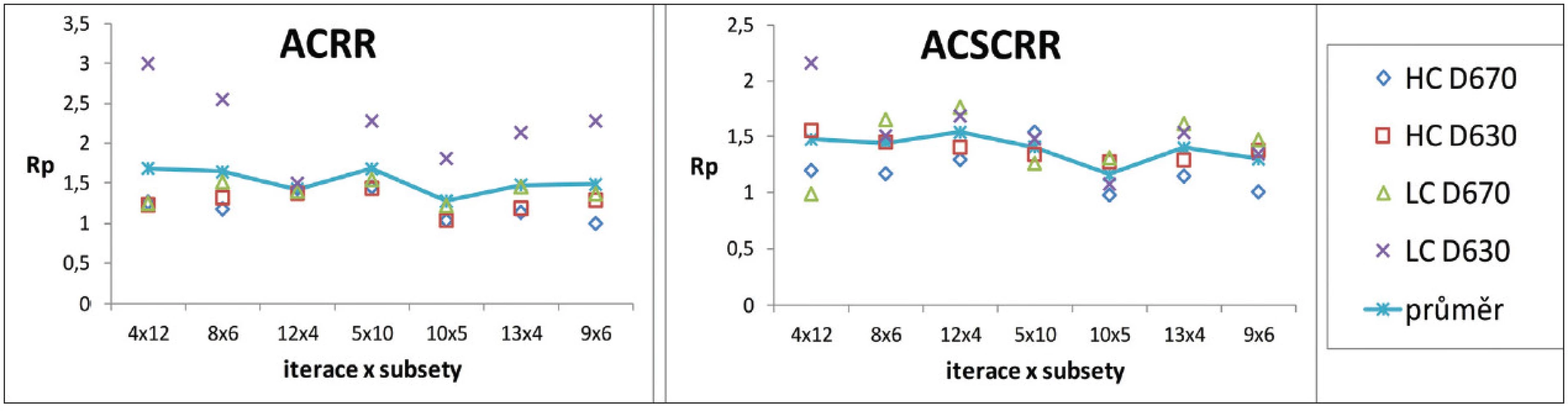
Obr. 5. Závislost relativního kontrastu na počtu efektivních iterací pro 4 nejmenší zkoumané léze po korekci na zeslabení bez resolution recovery algoritmu (vlevo) a s ním (vpravo) z měření vysokého kontrastu na GE Discovery 630. Kontrast je normovaný na maximální změřený kontrast pro danou lézi (odpovídá 100 %). Vyznačené jsou oblasti optimálního nastavení podle optimalizační míry R<sub>p</sub>. 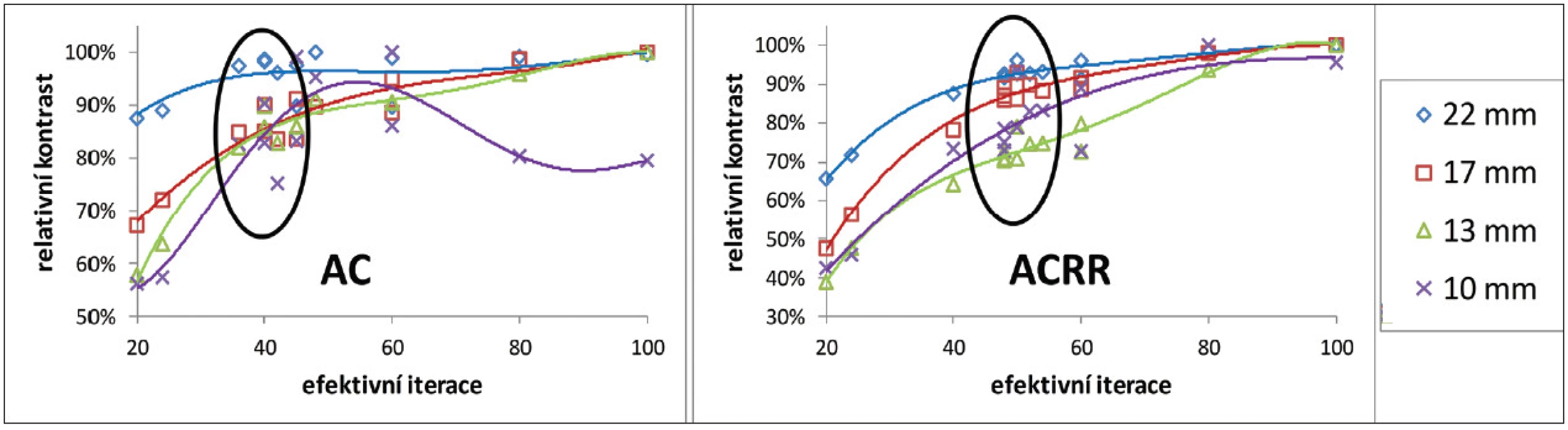
Obr. 6. Závislost relativního poměru signálu k šumu na počtu efektivních iterací pro 4 nejmenší zkoumané léze po korekci na zeslabení bez resolution recovery algoritmu (vlevo) a s ním (vpravo) z měření vysokého kontrastu na GE Discovery 630. Poměr signálu k šumu je normovaný na maximální změřený poměr signálu k šumu pro danou lézi (odpovídá 100 %). Vyznačené jsou oblasti optimálního nastavení podle optimalizační míry R<sub>p</sub>. 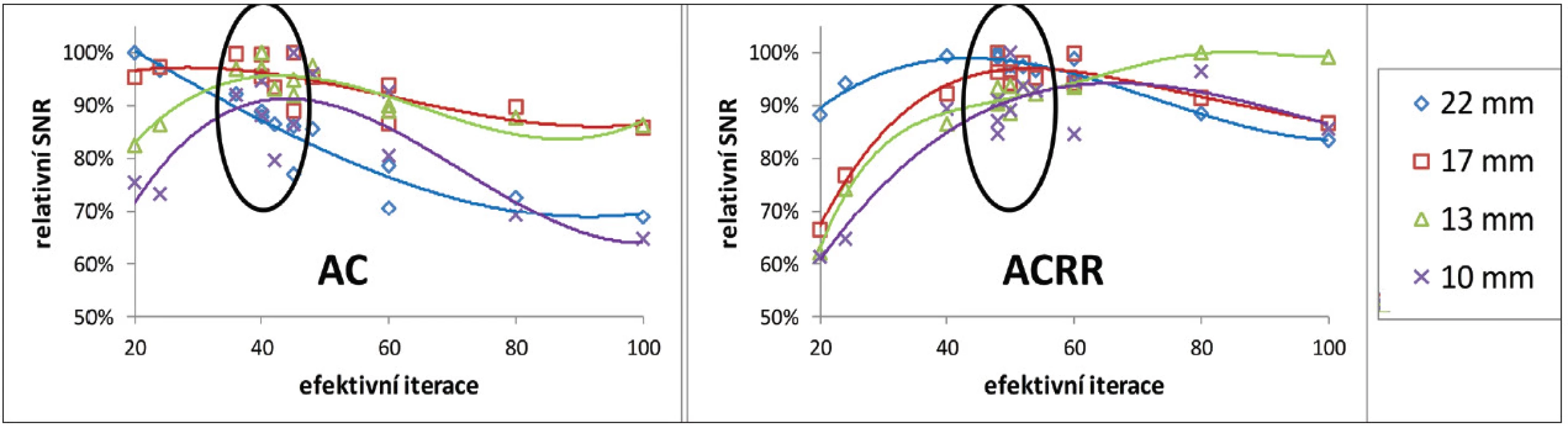
Diskuze
Provedení akvizice pouze v matici 256 x 256 a její softwarové upravení do menší matice sečtením čtyř sousedních pixelů nemá na výsledky vliv. Díky tomu, že počet detekovaných impulsů v pixelu má Poissonovo rozdělení 2, takto získaná data se také řídí Poissonovým rozdělením (součet náhodných veličin s Poissonovým rozdělením je náhodná veličina opět s Poissonovým rozdělením 7) a mají tedy stejné statistické vlastnosti, a tedy i šum, jako data, která bychom získali samostatnou akvizicí v menší matici.
Optimalizační veličina Rp má při rekonstrukci bez RR zřetelné minimum u všech korekcí v oblasti 30–50 efektivních iterací. (Obr. 1) V případě použití RR dochází ke stálému poklesu a minimum neexistuje v rekonstruované oblasti. Za optimální oblast pro RR bylo zvoleno 40–60 efektivních iterací, protože v tomto intervalu dochází k výrazné změně trendu poklesu. (Obr. 3) Toto chování je shodné pro HC i LC pro obě kamery. Nebyl nalezen výraznější rozdíl tvaru závislostí v matici 128 x 128 a 256 x 256. Nalezená optima byla srovnána s průběhem kontrastu, SNR a prostorového rozlišení.
S rostoucím počtem efektivních iterací roste kontrast, dokud nedosáhne svého maxima. (Obr. 5) Tato konvergence je rychlejší u větších lézí. Pokles kontrastu pro lézi velikosti 10 mm pro 80 a 100 efektivních iterací lze přisoudit šumu, který u ostatních měření nebyl přítomen. Relativní šum roste v rekonstruované oblasti téměř lineárně a u větších lézí vždy rychleji než kontrast, takže SNR klesá v celé rekonstruované oblasti; u malých lézí existuje maximum SNR v rekonstruované oblasti a poloha maxima závisí na velikosti léze. (Obr. 6) U algoritmu RR je patrná pomalejší konvergence kontrastu, ovšem k vyšším hodnotám než bez jeho použití. Pomalejší konvergence se projevuje posunem maxima SNR k vyššímu počtu efektivních iterací. Průběh prostorového rozlišení je výrazně odlišný pro RR algoritmus a bez něj. Bez RR prostorové rozlišení pro nízký počet efektivních iterací klesá, dokud nedosáhne svého minima v oblasti kolem 40 efektivních iterací a dále se už výrazně nemění. (Obr. 7) S RR algoritmem prostorové rozlišení monotónně klesá i pro vysoký počet efektivních iterací, nicméně je patrná změna trendu v oblasti 40–60 efektivních iterací.
Obr. 7. Prostorové rozlišení pro vysoký kontrast měřené na GE Discovery 630 v závislosti na počtu efektivních iterací pro různé korekce: bez korekce (NC), korekce na zeslabení (AC), korekce na rozptyl (SC) a s použitím resolution recovery algoritmu (RR). Vyznačeny jsou oblasti minima optimalizační míry R<sub>p</sub> pro rekonstrukce bez RR (plná čára) a s RR (čárkovaně). 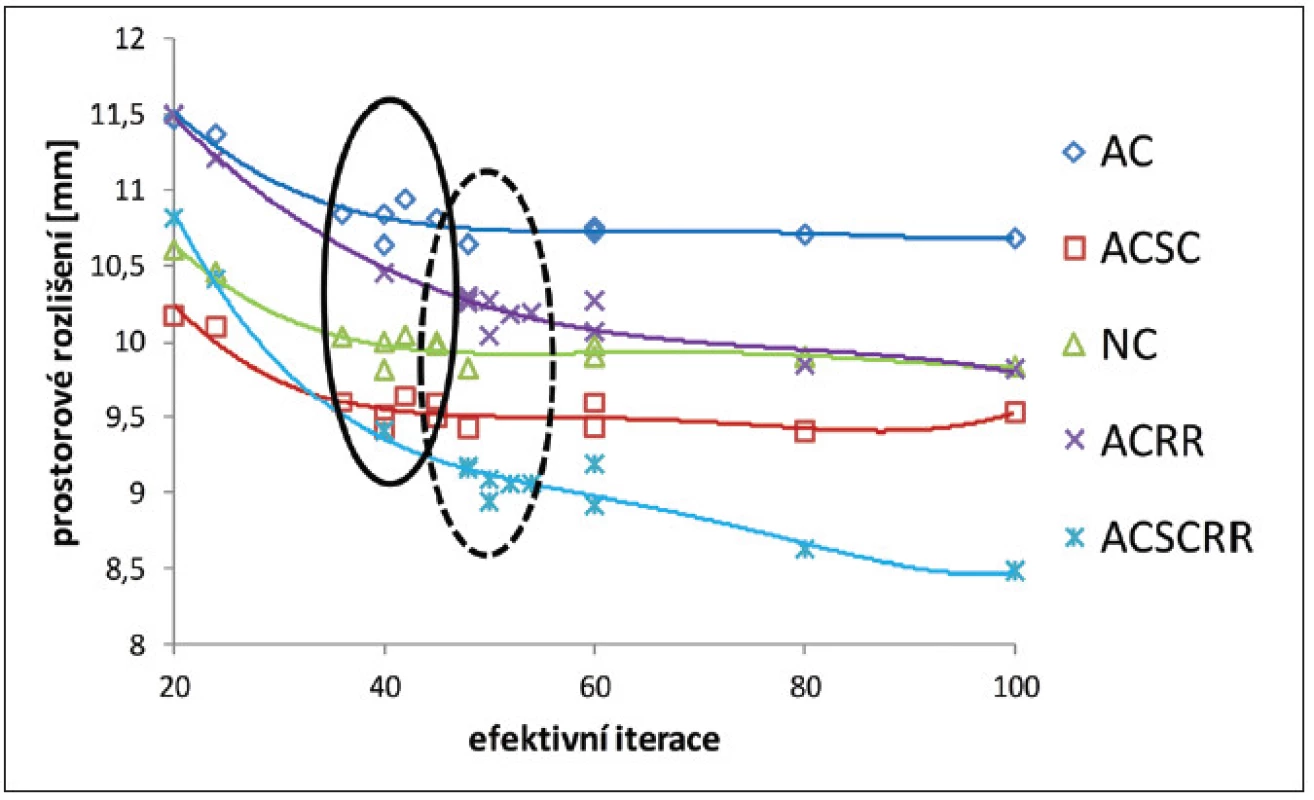
V klinické praxi je optimální obraz ten, který kromě objektivních měřitelných parametrů vyhovuje i subjektivnímu názoru hodnotících lékařů pro daný typ vyšetření, zejména z hlediska hladiny šumu. V ideálním případě by tedy optimalizace musela zahrnout i intenzivní spolupráci všech hodnotících lékařů. Pro zjednodušení a urychlení nebyl proto do optimalizace zahrnut postrekonstrukční filtr, optimalizace byla provedena pouze na základě objektivně měřitelných parametrů a výběr filtru byl ponechán na libovůli lékařů. Tím bylo zajištěno, že nefiltrovaný obraz dosáhne optimální kvality a lékaři si sami zvolí míru její degradace volbou postrekonstrukčního filtru v závislosti na typu vyšetření. Kromě toho by zahrnutí filtru výrazně prodloužilo celý proces optimalizace, protože každá změna parametrů filtru by umocnila počet možných kombinací parametrů a tedy i dobu nutnou k analýze.
Filtrace pro hledání lézí byla nutná, aby byla zajištěna stabilita neighbor-growing algoritmu a jeho pološířka byla zvolena empiricky tak, aby počet nalezených voxelů přibližně odpovídal objemu hledané léze.
Recovery koeficient i prostorové rozlišení úzce souvisí s kontrastem. Prostorové rozlišení lze stanovit z RC křivky, tzn. závislosti RC na velikosti léze. RC křivka, tedy poměr kontrastu změřeného a kontrastu teoretického, odpovídá modulační přenosové funkci 6, je tedy Fourierovou transformací odezvy bodového zdroje (PSF) vyjádřenou v x-prostoru (nikoliv v p-prostoru prostorových frekvencí Fourierovy transformace). (Obr. 8) Zvýšení kontrastu vede k takové úpravě tvaru RC křivky, která se projeví zúžením PSF a tedy zlepšením prostorového rozlišení. Optimalizace kontrastu pro všechny velikosti lézí tedy vede k optimalizaci prostorového rozlišení.
Obr. 8. Vztah mezi odezvou bodového zdroje (PSF), modulační přenosovou funkcí (MTF) a RC křivkou. 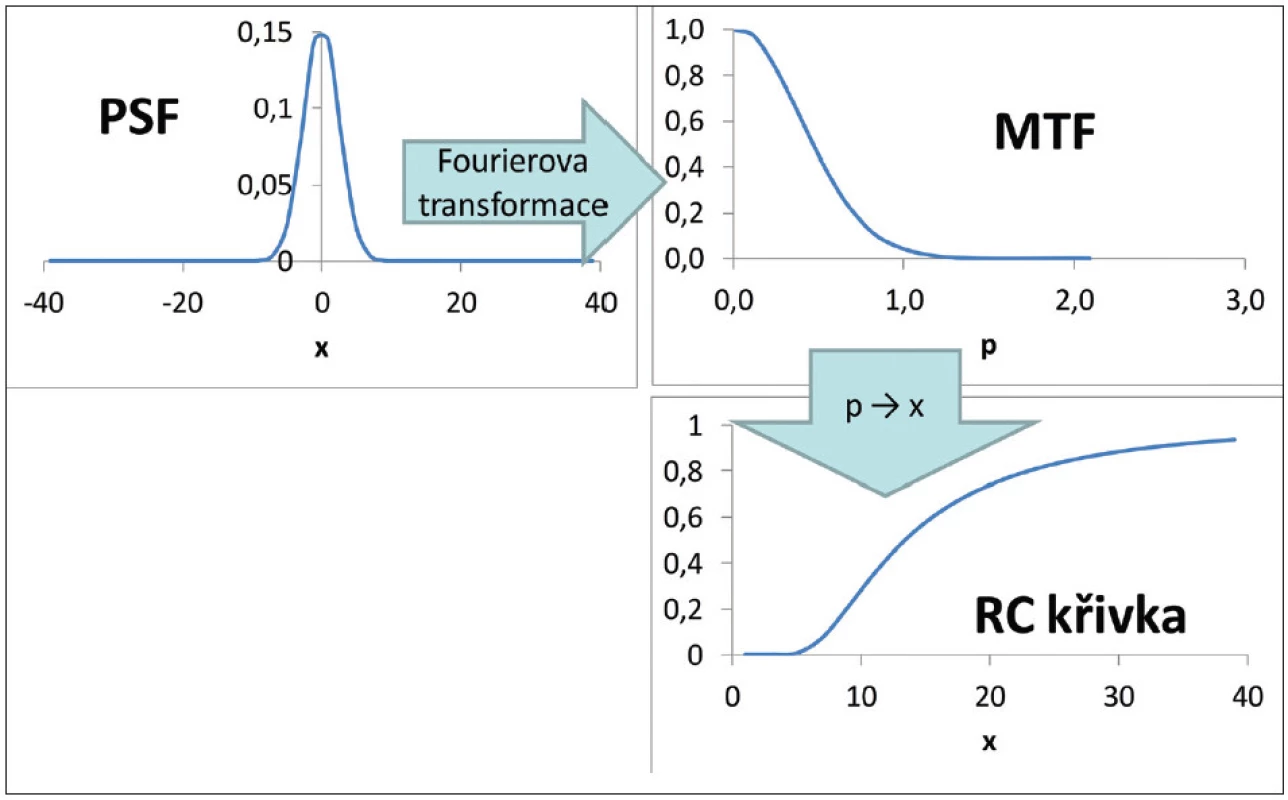
Jak SNR, tak kontrast ovlivňují detekovatelnost lézí (Obr. 9), a proto je nutné je do optimalizačního procesu zahrnout. Nicméně tyto veličiny samy o sobě nejsou vhodnými mírami pro optimalizaci. Kontrast s rostoucím počtem efektivních iterací (součinu počtu subsetů a počtu iterací) roste, jak rekonstruovaný obraz konverguje k maximálně věrohodnému řešení (srovnej s naměřeným kontrastem na Obr. 5).Svého maxima tedy dosahuje pro vysoké počty efektivních iterací, a pokud rekonstrukční algoritmus skutečně konverguje, pak je kontrast nejvyšší v nekonečnu. Na druhou stranu relativní šum s rostoucím počtem efektivních iterací roste, takže průběh SNR pro nízký počet efektivních iterací nelze snadno odhadnout, nicméně pro vysoký počet iterací klesá, protože kontrast je téměř konstantní (viz naměřený SNR na Obr. 6). SNR svého maxima tedy dosahuje pro nízký počet efektivních iterací.
Obr. 9. Ilustrace kvality zobrazení pro vysoký SNR a nízký kontrast (vlevo) a nízký SNR a vysoký kontrast (vpravo). Pro správnou detekci léze je nutné, aby obě veličiny byly dostatečně velké. Vzájemný vztah kontrastu a prostorového rozlišení byl v tomto příkladu zanedbán. 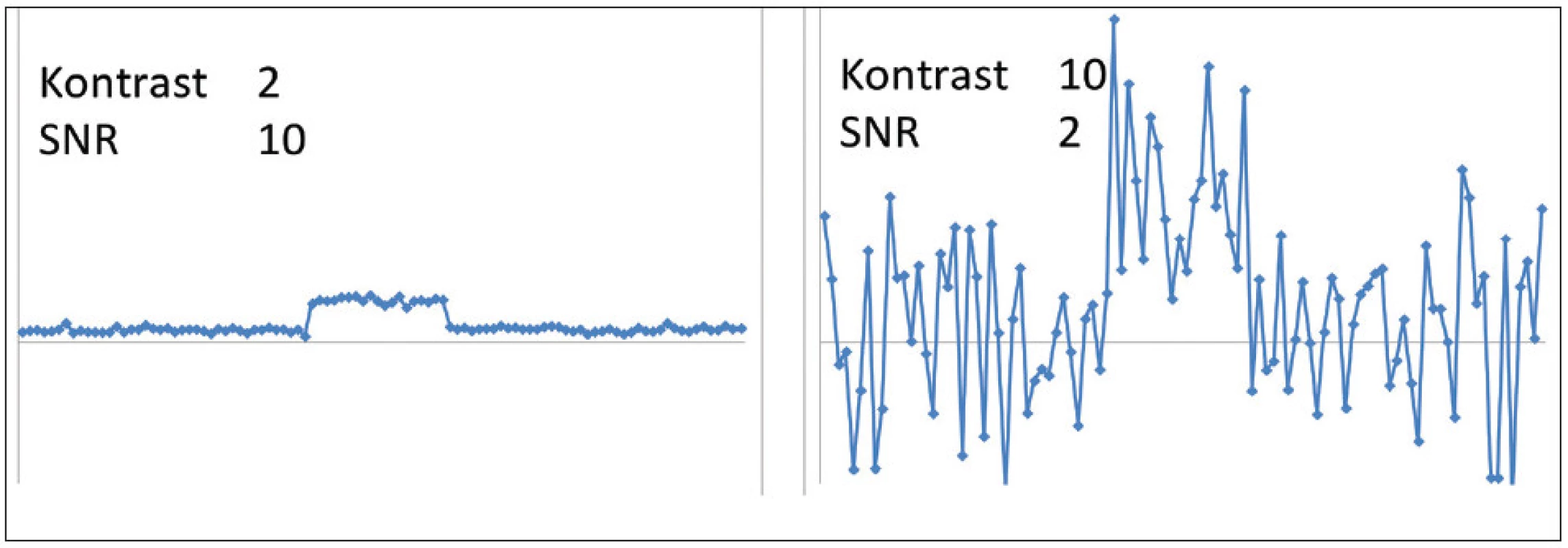
Obr. 10. Transversální řez fantomu z měření LC na Discovery 670 rekonstruovaný se všemi korekcemi ACSCRR pomocí 5 iterací a 10 subsetů bez filtru (A), vyhlazený Gaussovým filtrem o pološířce 1,75 pixelu (7,7 mm) (B) a 2 iterací a 10 subsetů bez filtru (C). 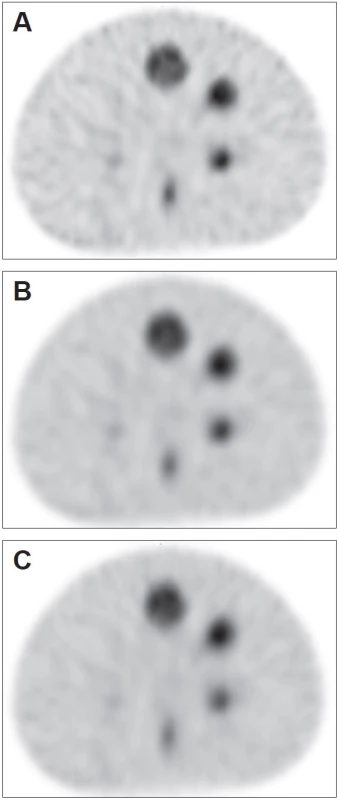
V dostupné literatuře se nepodařilo dohledat studii dospívající k jednoznačnému výsledku 8,9, která z veličin Rp a wv je v lidském vnímání pro detekovatelnost lézí podstatnější a jak velkou měrou, proto byly váhy wv položeny rovny jedné. V praxi to pak znamená, že jakákoliv změna parametrů z optimálních hodnot povede buď ke snížení obou veličin nebo ke zvýšení jedné a zároveň výraznějšímu snížení druhé. Váha wl odpovídá míře důležitosti schopnosti detekovat léze dané velikosti. Při volbě wl je nutné vždy přihlédnout ke vzorkování velikosti lézí v měřeném fantomu: v případě Body Fantomu v oblasti 1–2 mm leží 3 léze, v oblasti 2–3 mm 2 léze a v oblasti 3–4 mm jedna. Pokud by váhy wl byly rovny jedné, znamenalo by to, že příspěvek do sumy by byl trojnásobný pro velikosti lézí 1–2 mm oproti příspěvku lézí velikosti 3–4 mm a 1,5násobný oproti příspěvku lézí velikosti 2–3 mm. Volba vah wl = 1 pro objekty fantomu pak ve skutečnosti znamená váhy 3, 2 a 1 pro velikosti 1–2 mm, 2–3 mm a 3–4 mm. Při této optimalizaci byl kladen důraz na kvalitu zobrazení především malých lézí, a proto váhy wl byly zvoleny rovny jedné, takže malé objekty do optimalizace zasahují významnější měrou.
Veličinu Rp je nutné považovat pouze za pomocnou veličinu umožňující pomocí jedné hodnoty porovnat kvalitu obrazu pro různé rekonstrukce a efektivněji dospět do vhodné oblasti zájmu v parametrickém prostoru. Optimální nastavení je ale třeba vždy interpretovat z hlediska zavedených veličin jako kontrast, šum, SNR nebo prostorové rozlišení.
Protože nebyly nalezeny zásadní rozdíly mezi oběma kontrasty (HC, LC) ani oběma kamerami (D630, D670), a to ani pro AC (z nichž jedna byla provedena Changovou metodou a druhá na základě CT), pro výsledné hodnocení jsme pracovali s průměry sledovaných veličin z měření obou kamer a obou kontrastů.
Výběr optimálního nastavení podle Rp odpovídá oblasti těsně před dosažením maxima kontrastu, oblasti maxima SNR nejmenších lézí a oblasti změny trendu poklesu prostorového rozlišení.
Volba konkrétní kombinace počtu subsetů a iterací není z dat zcela jednoznačná – nelze vysledovat jednoznačnou závislost Rp ani na počtu iterací pro konstantní počet subsetů, ani na počtu subsetů pro konstantní počet iterací a rozdíly hodnot Rp mezi jednotlivými kombinacemi jsou malé. Do konečného výběru optimální kombinace jsme proto zohlednili také výpočetní čas, který roste výrazněji s rostoucím počtem iterací než s rostoucím počtem subsetů, takže rychlejší rekonstrukce je vždy pro kombinaci s nižším počtem iterací. Abychom omezili možnost vzniku artefaktů, vyřadili jsme také ty kombinace, u nichž by počet projekcí v každém subsetu byl nižší nebo roven třem, tzn. počet subsetů by byl vyšší nebo roven dvaceti. Protože nejčastěji využívanou korekcí v klinické praxi na Klinice nukleární medicíny FNOL je korekce na zeslabení, za optimální nastavení jsme zvolili pro matici 128 x 128 4 iterace a 10 subsetů pro rekonstrukce bez RR (srovnej s Obr. 2) a 5 iterací a 10 subsetů při použití RR (srovnej s Obr. 4). V matici 256 x 256 byl rekonstrukční program pro některé konfigurace nestabilní, a proto za optimální nastavení byly zvoleny 3 iterace a 12 subsetů bez RR a 4 iterace a 12 subsetů při použití RR.
Poloha minima optimalizační míry Rp pro rekonstrukce bez RR odpovídá velmi dobře oblasti, která se z hlediska kontrastu, SNR i prostorového rozlišení jeví jako optimální. Její použití jako prostředku pro matematické zpracování dat a rychlejší nalezení optima se tedy jeví jako vhodné. V případě RR minimum Rp ve sledované oblasti parametrického prostoru neexistuje, a proto je využití veličiny Rp v tomto případě diskutabilní. Velmi vhodné by bylo doplnění váhy wv v definici Rp na základě objektivní studie, tedy porovnání vlivu objektivně měřených veličin jako kontrast a SNR na lidské vnímání kvality obrazu a jeho schopnosti nalézt případné léze. Změna hodnoty wv může mít vliv na výsledek optimalizace. Volba vah wl může mít také vliv, protože chování objektů o různé velikosti je při rekonstrukcích odlišné. Z naměřených závislostí kontrastu a SNR by však tyto vlivy pro hodnoty vah ne příliš vzdálené od jedné neměly být příliš významné.
Prostorové rozlišení bylo určeno na základě tvaru RC křivky. Tato metoda je zatížena velkou chybou měření a prostorové rozlišení je silně závislé na přesnosti nalezení oblasti lézí. V porovnání s hodnotou prostorového rozlišení určeného přímým měřením jsou takto určené hodnoty systematicky nadhodnocené. Nicméně lze předpokládat, že toto nadhodnocení je pro všechny rekonstrukce přibližně stejné, takže tvar závislosti na počtu efektivních iterací by měl být zachován.
Nalezené optimum je blízké konfiguraci používané na původních kamerách na základě několikaletých zkušeností. Výrobcem doporučené nastavení 2 iterací a 10 subsetů 10 se nezdá být příliš vhodné (Obr. 5, 6 a 7), zejména v kombinaci s RR algoritmem.
Pro ilustraci jsou uvedeny tytéž transverzální řezy z měření LC na Discovery 670 rekonstruované se všemi korekcemi ACSCRR se 2 iteracemi a 10 subsety a 5 iteracemi a 10 subsety. (Obr. 10) Uvedeny jsou nefiltrované obrazy pro obě nastavení a navíc pro 5 iterací a 10 subsetů obraz vyhlazený Gaussovým filtrem s pološířkou 1,75 pixelu (7,7 mm) tak, aby celkový šum v obraze byl stejný jako u obrazu rekonstruovaného pomocí 2 iterací a 10 subsetů bez filtru. Kvalitu rekonstruovaného obrazu lze volbou vhodného filtru snížit přibližně na úroveň obrazu rekonstruovaného pomocí nižšího počtu efektivních iterací. Výhodou vyššího počtu efektivních iterací je tedy širší možnost ovlivňování úrovně a charakteru šumu pomocí různě nastavených filtrů. Volba klinicky používaného filtru by také měla být výsledkem nějakého optimalizačního procesu.
Závěr
Byla provedena optimalizace nastavení počtu iterací a počtu subsetů rekonstrukce OSEM na základě relativní odchylky od změřeného maxima kontrastu a SNR pro různé korekce a resolution recovery algoritmus pro různé kontrasty měřených aktivit na dvou typech kamer stejné řady téhož výrobce. Optimální nastavení bylo srovnáno s průběhy kontrastu, SNR a prostorového rozlišení v závislosti na počtu efektivních iterací. Analýza byla založena na více než 500 rekonstrukcích.
S přihlédnutím ke stabilitě rekonstrukčního programu, výpočetnímu času a možnosti vzniku artefaktů při příliš nízkém počtu projekcí v subsetu byly vybrány optimální konfigurace: 4 iterace a 10 subsetů pro rekonstrukce bez RR v a 5 iterací a 10 subsetů při použití RR v matici 128 x 128, 3 iterace a 12 subsetů bez RR a 4 iterace a 12 subsetů při použití RR v matici 256 x 256.
pavel.karhan@fnol.cz
Zdroje
1. SÚJB. Systém zabezpečení jakosti na pracovištích nukleární medicíny – přístrojová technika. Praha – Zbraslav, NUKLIN, 1999, 47 p
2. IAEA. Quality assurance for SPECT systems. Vídeň, IAEA, 2009, 250 p
3. NEMA NU 2-2007 IEC Body Phantom, Model PET/IEC-BODY/P
4. Xeleris Functional Imaging Workstation – verze 3.1. General Electric Company, 2013
5. Anděl J. Základy matematické statistiky. Praha, Matfyzpress, 2011, 358 p
6. Drastich, A. Netelevizní zobrazovací systémy. Brno, VUT Brno, 2001, 174 p
7. Boellaard R, Delgado-Bolton R, Oyen WJ et al. FDG PET and PET/CT: EANM procedure guidelines for tumour PET imaging: version 1.0. Eur J Nucl Med Mol Imaging 2010;37 : 181–200
8. Farquhar TH, Llacer J, Sayre J et al. ROC and LROC Analyses of the Effects of Lesion Contrast, Size, and Signal-to-Noise Ratio on Detectability in PET Images. J Nucl Med 2000;41 : 745–754
9. Puff DT. Human vs. Vision Model Performance for Two Medical Image Estimation Tasks. Dizertační práce University of North Carolina at Chapel Hill, Department of Computer Science [online]. 1995. [cit. 2015-08-22]. Dostupné na: http://www.cs.unc.edu/xcms/techreports/techreports.html jako Technical Report TR95-027
10. manuál Xeleris 3.1
Štítky
Nukleárna medicína Rádiodiagnostika Rádioterapia
Článok vyšiel v časopiseNukleární medicína

2015 Číslo 4
Najčítanejšie v tomto čísle- Extraneurálna diseminácia cerebelárneho meduloblastómu vizualizovaná pomocou PET/CT s 18F-FDG, kazuistika zriedkavého prípadu
- Optimalizace rekonstrukčních parametrů pro SPECT a SPECT/CT
-
O JAKÉ VYŠETŘENÍ SE JEDNÁ?
JAKÁ JE VAŠE INTERPRETACE TĚCHTO OBRÁZKŮ?
Prihlásenie#ADS_BOTTOM_SCRIPTS#Zabudnuté hesloZadajte e-mailovú adresu, s ktorou ste vytvárali účet. Budú Vám na ňu zasielané informácie k nastaveniu nového hesla.
- Časopisy