-
Články
- Časopisy
- Kurzy
- Témy
- Kongresy
- Videa
- Podcasty
Analýza dat v neurologii
XVI. Zlatý standard statistického testování: t‑test
Autoři: L. Dušek; T. Pavlík; J. Koptíková
Působiště autorů: Institut biostatistiky a analýz, Masarykova univerzita, Brno
Vyšlo v časopise: Cesk Slov Neurol N 2009; 72/105(4): 389-393
Kategorie: Okénko statistika
Asi bychom mezi čtenáři těžko hledali někoho, kdo by neznal t‑test jako standard pro srovnávání dvou průměrů. T-test využívající testovou statistiku, která má Studentovo t rozdělení, určitě patří mezi nejpoužívanější testy v biostatistice. V tomto díle seriálu tedy nemáme ambici přinést pro čtenáře něco zcela nového, spíše se pokusíme výklad o t‑testu pragmaticky a přehledně uspořádat. I tento jednoduchý test má své předpoklady a pravidla, jejichž nerespektování může vést k vážným zkreslením.
Nejprve si ale musíme uvědomit, že pod souhrnným názvem „t‑test“ se v podstatě skrývá několik variant testu s rozdílným významem a interpretací. Zdůrazňování tohoto faktu je zvlášť důležité ve věku osobních počítačů, kdy uživatel statistického programu spouští proceduru jediným stiskem klávesy „enter“. Může tak lehce opominout důležité předpoklady nebo přímo vybrat nesprávný test, který s danými daty buď nepůjde vůbec realizovat, anebo povede ke zcela nesmyslnému závěru. Nadto různé t‑testy bývají často na různých místech nabídky software, a uživatel tak musí vědět, který chce zvolit, a aktivně si jej vyhledat.
Popis variant t‑testu můžeme využít ke krátkému seznámení s jednovýběrovým a dvouvýběrovým experimentálním uspořádáním (obr. 1). Jednovýběrové testování pracuje s jedním náhodným výběrem o n opakováních, který vede k výběrovému rozdělení s určitou střední hodnotou. Jednovýběrový t‑test ověřuje, zda odhad této střední hodnoty nabývá určité konkrétní hodnoty (dáno jako konstanta). Předpokladem je normální rozdělení sledované veličiny. Dvouvýběrový t‑test pracuje se dvěma normálními rozděleními a ověřuje, zda mají stejné střední hodnoty. Toto uspořádání předpokládá provedení dvou náhodných výběrů, které jsou vzájemně nezávislé a mohou mít i různou velikost. Zvláštním typem uspořádání je srovnávání dvojic hodnot, které k sobě mají nějaký vztah (např. hodnota parametru X měřená u téhož pacienta před operací a po ní). U dvojic takto provázaných hodnot logicky sledujeme jejich rozdíly, resp. posuzujeme, zda střední hodnota jejich rozdílů je rovna určitému číslu. Je‑li rovna nule, původní dvojice se v průměru neliší. U takového výpočtu hovoříme o párovém t‑testu.
Obr. 1. Schéma experimentálních uspořádání, které vedou k různým variantám <i>t</i>-testu. 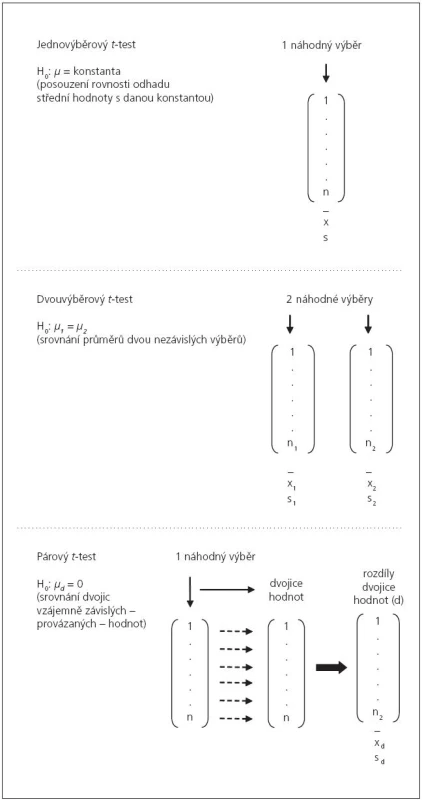
Jak vidno, existují tři základní varianty t‑testu. Každý hodnotí zcela jinou experimentální situaci a jinou vstupní nulovou hypotézu (obr. 1, tab. 1). Párový t‑test vede k výpočtu, který pracuje s rozdíly původně naměřených dvojic hodnot, a konečný výpočet je tak shodný s jednovýběrovým testem. Všechny varianty t‑testu spojuje řada charakteristik:
- Univerzálním předpokladem je provedení náhodného výběru z normálního rozdělení. Tento předpoklad je nutné ověřovat především u malých vzorků, kde hrozí i zvýšený vliv odlehlých hodnot.
- Vzhledem k předpokladu normálního rozdělení jsou všechny varianty t‑testu parametrické. Pracujeme s aritmetickým průměrem jako odhadem střední hodnoty normálního rozdělení. Aritmetický průměr má sám o sobě normální výběrové rozdělení. V předchozích dílech jsme dokládali, jaký dopad má na výpočet aritmetického průměru asymetrie výběrového rozdělení nebo přítomnost odlehlých extrémních hodnot. V takových případech nemá už sám aritmetický průměr interpretační význam, a nemá tudíž smysl ani jakýkoli test o něm.
- T-testy mají svůj název odvozen od konečné testové statistiky, která má Studentovo t rozdělení. Výpočet testovacího kritéria t vychází z odhadů parametrů μ a σ u výběrových souborů: –x a s. Vypočtené testovací kritérium porovnáme s tabulkovou kritickou hodnotou (1 – α/2 kvantil Studentova rozdělení pro dané ν a zvolené α). Hodnota ν označuje stupně volnosti daného rozdělení t (tab. 1) a je jediným parametrem Studentova rozdělení (jednoduše řečeno podle ν hledáme v tabulkách). Pokud pracujeme s velkými výběry (n v řádu stovek a více), můžeme namísto kritických hodnot rozdělení t použít přímo kritické hodnoty normálního rozdělení z.
Tab. 1. Přehled variant t-testu. 
Jsme přesvědčeni, že i ve světě osobních počítačů a samostatně pracujících statistických programů má smysl znát postup výpočtu nejčastěji používaných testů. Proto na příkladech 1 až 3 demonstrujeme výpočet jednotlivých variant t‑testu. V dalším textu shrnujeme některé podstatné metodické poznámky.
Jednovýběrový t‑test:
- V tomto případě stojíme před úkolem srovnat průměrnou hodnotu n měření (jeden náhodný vzorek) s danou hodnotou, která představuje nějakou normativně danou hranici nebo předpoklad. V podstatě tak ověřujeme, zda provedený výběr patří svou střední hodnotou do základního souboru se středem, který určuje daná konstanta.
- V praxi jde o typický příklad, kdy ověřujeme, zda se opakované měření nějakého znaku v průměru neodchyluje od stanovené hodnoty (konstanty). Jiným příkladem může být test, zda se průměr n měření nějaké látky neliší od normou dané hodnoty.
Příklad 1. Jednovýběrový <i>t</i>-test pro srovnání průměrné hmotnosti souboru pacientů s danou populační hodnotou. 
Dvouvýběrový t‑test (dva nezávislé výběry):
- Úkolem je srovnat průměry dvou náhodných výběrů, které byly získány zcela nezávisle jeden na druhém. Tedy výběr jedinců (subjektů) v jednom výběru nijak nesouvisí s výběrem v druhém výběru, a to ani pořadím, jak byli vybíráni. Oba výběry mohou mít rozdílný počet měření (n1 ≠ n2); příliš velké rozdíly ve velikosti výběru se ale nedoporučují, neboť takové odhady průměru jsou obtížně srovnatelné z hlediska variability.
- Předpokladem je, že náhodné výběry mají normální rozdělení, a tento předpoklad je nutno ověřit u každého z obou výběrů samostatně, neboť do výpočtu vstupují jako nezávislé vzorky s odhadem aritmetického průměru a směrodatné odchylky (příklad 2).
- Příklad 2 popisuje situaci, kdy se rozptyly obou výběrů neliší. Pokud by variabilita v srovnávaných výběrech byla významně rozdílná, je nutné použít jiný postup, který podrobně popíšeme v dalším díle našeho seriálu.
Příklad 2. Dvouvýběrový <i>t</i>-test pro srovnání hmotnosti dvou souborů pacientů. 
Párový t‑test:
- Test srovnávající posun hodnot ve dvojici vzájemně nějak souvisejících (závislých) výběrů. V podstatě jde o stejné srovnání jako u dvouvýběrového testu, i zde máme na vstupu dva výběry. Zásadní rozdíl je ale v tom, že u párového uspořádání nebyl druhý vzorek vybírán náhodně, ale v souvislosti s prvním měřením. Základní otázka zde je, „o kolik“ se liší tyto dvojice čísel a výpočet směřuje k jejich odečtení a hodnocení jejich rozdílů (obr. 1, příklad 3).
- Předpoklad normálního rozdělení zde tedy platí až pro rozdíly původních hodnot, protože i samotný výpočet pracuje pouze s těmito rozdíly.
- Typickým příkladem párového uspořádání je měření parametru na témže jedinci před nějakou změnou a po ní (experimentu), před léčebným výkonem a po něm apod. Dalším příkladem mohou být plánovitá měření na párových orgánech, které srovnáváme vždy na témže jedinci.
Příklad 3. Párový <i>t</i>-test pro srovnání hmotnosti souboru pacientů před a po redukční dietě. 
Je patrné, že o tom, jaký bude použit t‑test, rozhoduje již sám experimentátor tím, jaký zvolí postup. Není to primárně odpovědnost statistika, naopak. A také bohužel platí, že mají‑li dva výběry stejný počet opakování (n1 = n2), můžeme na nich současně provést výpočet dvouvýběrového i párového t‑testu. Velmi pravděpodobně ovšem s různým výsledkem, protože každý testuje něco jiného:
- Dvouvýběrový test srovnává aritmetické průměry dvou zcela nezávislých populací. Pracujeme zde přímo s primárními hodnotami a ve výpočtu srovnáváme dva nezávislé odhady průměrů. Do výpočtu přímo vstupují výběrové odhady směrodatných odchylek s1 a s2. Konečná statistika t má počet stupňů volnosti ν = n1 + n2 – 2.
- Párový test sleduje, o kolik se změnila průměrná hodnota v téže populaci po nějaké změně. Hodnoty naměřené před touto událostí a po ní jsou odečteny a je hodnocen průměr takto získaných rozdílů. Variabilita původních měření do výpočtu nevstupuje, pracujeme se směrodatnou odchylkou rozdílů (sd), která bude v převážné většině případů menší než směrodatná odchylka původních měření. Počet stupňů volnosti pro konečnou statistiku t počítáme stejně jako u jednovýběrového t‑testu, ν = n – 1.
Příklad 4 znázorňuje situaci, kdy na data z jednoho experimentu můžeme současně použít dvouvýběrový i párový t‑test. Zatímco dvouvýběrový test neprokazuje statisticky významný rozdíl mezi dvěma výběrovými průměry, párový t‑test ukazuje, že průměrný rozdíl obou výběrů je významně rozdílný od nuly. Jelikož experimentální uspořádání je v příkladu 4 jednoznačně párové, správné je hodnocení párovým testem. Dvouvýběrový test nelze použít již vzhledem k tomu, že druhé měření není nezávislé na prvním; je provedeno na stejných jedincích po realizovaném experimentu. Bohužel uživatel statistického programu, který tyto skutečnosti nezná, může lehce zvolit chybný test. Snad i tento náš seriál přispěje k tomu, že se to čtenářům ČSNN nestane☺.
Příklad 4. Modelové srovnání dvouvýběrového <i>t</i>-testu a párového <i>t</i>-testu na stejných datech. 
Závěrem nelze odolat pokušení alespoň se zmínit o tom, komu vlastně vděčíme za t‑test, který je také někdy nazýván „Studentův t‑test“ (jelikož využívá Studentovo t rozdělení). Jeho autor se totiž nejmenoval Student a nejde ani o název věnovaný altruisticky studentům statistiky. Autorem je chemik a statistik W. S. Gosset (1876–1937), který pracoval v pivovaru Guinness. Zde měl za úkol srovnávat kvalitu jednotlivých várek piva a vyvíjet procedury, které by zaručovaly standardní testování kvality. T-test vyvinul jako postup pro porovnávání obsahu kvasinek v jednotlivých várkách s nastaveným standardem. A jelikož si vedení pivovaru nepřálo veřejné publikace výzkumných výsledků svých zaměstnanců, pilný pan Gosset sdělil své objevy lidstvu pod pseudonymem „Student“. Jak je zřejmé, vědecké poznání si vždy cestu najde. Čtenářům tedy na konci této kapitoly můžeme doporučit skvělý vychlazený Guinness jako odměnu za jejich trpělivost při studiu ☺.
doc. RNDr. Ladislav Dušek, Dr.
Institut biostatistiky a analýz
Masarykova univerzita, Brno
e-mail: dusek@cba.muni.cz
Štítky
Detská neurológia Neurochirurgia Neurológia
Článok vyšiel v časopiseČeská a slovenská neurologie a neurochirurgie
Najčítanejšie tento týždeň
2009 Číslo 4- Metamizol jako analgetikum první volby: kdy, pro koho, jak a proč?
- Kombinace metamizol/paracetamol v léčbě pooperační bolesti u zákroků v rámci jednodenní chirurgie
- Antidepresivní efekt kombinovaného analgetika tramadolu s paracetamolem
- Neuromultivit v terapii neuropatií, neuritid a neuralgií u dospělých pacientů
- Srovnání analgetické účinnosti metamizolu s ibuprofenem po extrakci třetí stoličky
-
Všetky články tohto čísla
- Editori al
- Nádory tretej mozgovej komory
- Botulotoxin v léčbě spasticity
- Po užití metod magnetické rezonance pro poso uzení cerebrovaskulární rezervní kapacity
- Přání k významnému životnímu jubileu
- Eti ologi e a epidemi ologi e purulentní meningitidy u dospělých paci entů
- Změny parametrů páteře po implantaci bederní interspinózní rozpěrky DIAM
- Analýza psychologického profilu a spánkových vide o- EEG u dětí s vývojovo u dysfázi í
- Bimanu ální sekvenční motorická úloha u roztro ušené sklerózy mozkomíšní v obraze funkční magnetické rezonance: vliv fyzioterapeutických technik – pilotní studie
- Hodnocení cerebrovaskulární rezervní kapacity po EC- IC bypassu pomocí TCD
- Elektrotaktilní stimulace jazyka: nová možnost rehabilitace posturální stability – kazuistika
- Paroxysmální kinezigenní dyskineze: případ mladé ženy s alternující hemidystoni í – kazuistika
- Získaná neuromyotonie s nevelkými centrálními příznaky s průkazem protilátek proti napěťově řízeným kaliovým kanálům – kazuistika
- Zlepšení sledovacích pohybů očí a fonace po selektivní dorzální rizotomii
- Multimodální monitorování mozku u pacientů s těžkým kraniocerebrálním traumatem a subarachnoidálním krvácením v neuro intenzivní péči
- Webové okénko
-
Analýza dat v neurologii
XVI. Zlatý standard statistického testování: t‑test
- Zpráva z kurzu mikrodialýzy v Praze
- Česká a slovenská neurologie a neurochirurgie
- Archív čísel
- Aktuálne číslo
- Informácie o časopise
Najčítanejšie v tomto čísle- Nádory tretej mozgovej komory
- Získaná neuromyotonie s nevelkými centrálními příznaky s průkazem protilátek proti napěťově řízeným kaliovým kanálům – kazuistika
- Botulotoxin v léčbě spasticity
- Paroxysmální kinezigenní dyskineze: případ mladé ženy s alternující hemidystoni í – kazuistika
Prihlásenie#ADS_BOTTOM_SCRIPTS#Zabudnuté hesloZadajte e-mailovú adresu, s ktorou ste vytvárali účet. Budú Vám na ňu zasielané informácie k nastaveniu nového hesla.
- Časopisy



