-
Články
- Časopisy
- Kurzy
- Témy
- Kongresy
- Videa
- Podcasty
Analýza dat v neurologii XXIII.
Kontingenční tabulky neslouží jen pro testy hypotézy o nezávislosti znaků
Autoři: L. Dušek; T. Pavlík; Jiří Jarkovský
; J. Koptíková
Působiště autorů: Institut biostatistiky a analýz, Masarykova univerzita, Brno
Vyšlo v časopise: Cesk Slov Neurol N 2010; 73/106(5): 591-594
Kategorie: Okénko statistika
V předchozích dílech seriálu jsme se věnovali hodnocení hypotézy o nezávislosti dvou kategoriálních znaků. Tyto analýzy jsou postaveny na tabulkách četností obsahujících počty jedinců, u kterých sledujeme výskyt dvou znaků. Znaky mohou být binární (ano/ne) nebo kategoriální a podle toho je výsledkem tabulka velikosti 2 × 2 nebo větší. Jako příklad uveďme hodnocení nezávislosti tří druhů nemocí (znak A, kategoriální) a výskytu anémie u pacientů (znak B, binární).
Testy hypotézy o nezávislosti dvou znaků (proměnných) jsou nejčastějším využitím kontingenčních tabulek, avšak nikoli jediným. Další možnosti analýz závisí na způsobu, jak a za jakým účelem byly pozorované četnosti sbírány. Test hypotézy o nezávislosti (díl XXI) totiž vyžaduje, aby oba znaky byly sledovány zcela rovnocenně a nezávisle. U každého prvku (jedince) v náhodném výběru o velikosti N jsou současně a jednorázově zjišťovány kategorie obou znaků. Při sběru dat za tímto účelem považujeme oba znaky za zcela rovnocenné a jejich hodnocení nepodmiňujeme žádnými předpoklady o jejich vztahu. Ostatně právě jejich vztah je předmětem hodnocení.
Jiným příkladem využití kontingenční tabulky je tzv. test hypotézy homogenity. Odborně řečeno, jde o hodnocení podmíněných rozdělení jedné proměnné v rámci kategorií proměnné druhé. V české literatuře někdy též nalezneme termín testování hypotézy o shodnosti struktury. Jedna z proměnných vystupuje jako třídicí (stratifikační) faktor pro druhou proměnnou. Zde tedy nepřistupujeme ke znakům rovnocenně, neboť nás zajímá výskyt kategorií jednoho znaku proti znaku druhému. Třídicí proměnnou již při samotném sběru dat kontrolujeme, neboť v rámci jejích kategorií provádíme sledování proměnné druhé. Příkladem může být sledování, zda se dvě skupiny pacientů (diagnózy A, B) liší věkovou strukturou, kterou vyjádříme pěti kategoriemi (< 35 let, 36–45 let, …, > 65 let). Výsledná tabulka četností 2 × 5 obsahuje počty pacientů ve věkových třídách v rámci dvou skupin daných diagnózami A, B. Nutným předpokladem hodnocení je náhodný výběr každé subpopulace určené třídicím faktorem.
Je evidentní, že testy homogenity pracují s hypotézou rovnosti řádkových anebo sloupcových relativních četností v kontingenční tabulce. Vhodným nástrojem je v tomto případě binomický test, srovnávající dvě relativní četnosti, ovšem hodnocení hypotézy homogenity lze provést i „klasickým“ testem pro kontingenční tabulku s využitím statistiky χ2. O binomickém testu se nezmiňujeme v našem seriálu poprvé, v jeho nejjednodušší podobě jsme jej popsali v díle XIV. Zde v příkladu 1 uvádíme složitější výpočet, který dokumentuje hodnocení homogenity šesti nezávislých výběrů pacientů z různých nemocnic. U pacientů sledujeme výskyt komplikace X (ano/ne) a výsledkem je tedy tabulka četností 6 × 2. Nemocnice vystupuje v roli kontrolovaného, třídicího faktoru. Testujeme, zda se výběry z nemocnic shodují v relativním výskytu znaku X a pokud ne, tak které nemocnice se vzájemně shodují a které nikoli. Obdobně lze řešit i sumarizaci dat z literatury. Studujeme-li výskyt komplikace X u léčených pacientů a získáme výsledky od několika autorů, logicky je každé sledování na jiné populaci o jiné velikosti N. Test homogenity potom provádíme stejným postupem jako u nemocnic v příkladu 1. Pokud testem potvrdíme platnost hypotézy homogenity, můžeme příslušné kategorie třídicího znaku sloučit a četnost znaku popisovat na spojeném souboru.
Příklad 1. Test homogenity relativních četností ve vícenásobných nezávislých výběrech. 
Tab. 1 představuje tabulku četností, která je základem pro hodnocení nezávislosti výskytu znaků a hypotézy homogenity. Podstatné je, že oba typy testů lze provést na naprosto stejných datech. A pokud využijeme statistiku χ2, pak i stejným testovacím postupem. V obou případech je vstupem tabulka četností 2 × 2 nebo větší. Správná volba výpočtu a interpretace výsledku se tedy odvíjí od znalosti daného problému a od způsobu sběru dat. Počítačové programy v tomto příliš nepomohou, zde je úloha analytika dat nezastupitelná.
Tab. 1. Příklad tabulky četností dvou binárních proměnných nabývajících hodnot 1/0. 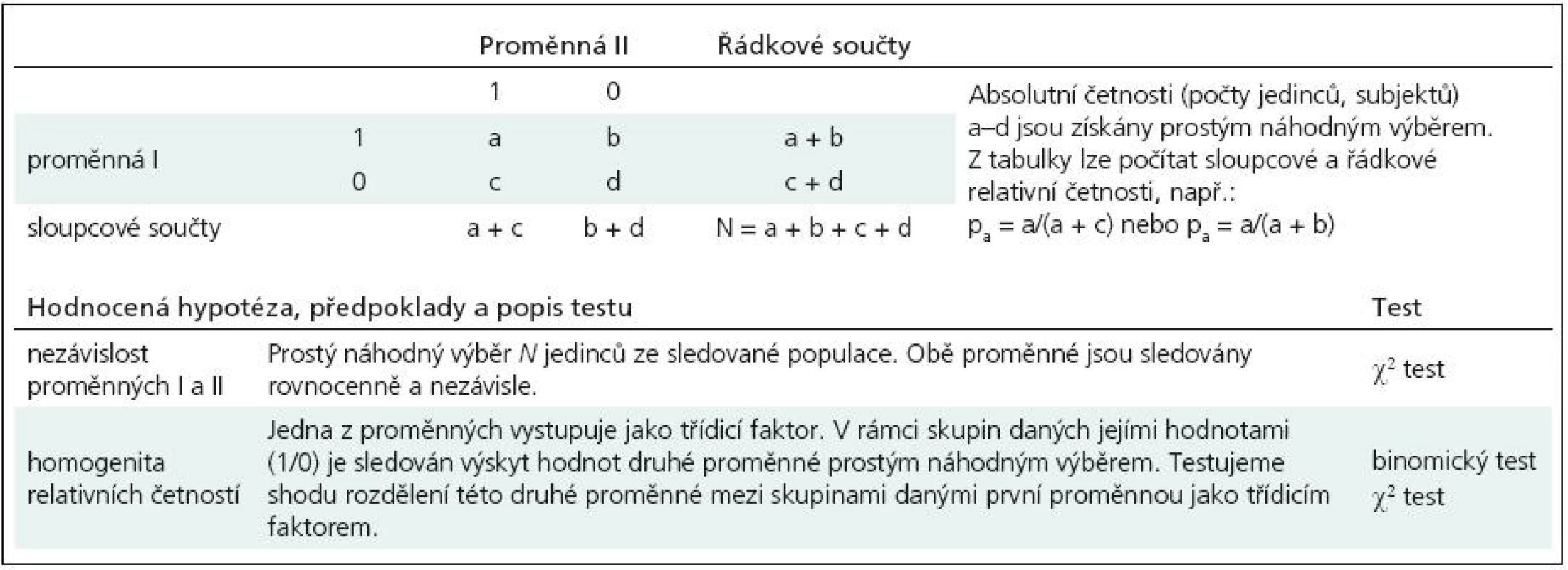
Jiný přístup k hodnocení tabulek četností představuje test hypotézy o symetrii neboli hodnocení binárních proměnných při párovém uspořádání experimentu. V zahraniční literatuře se často používá označení „categorical data observed in matched pairs“. Při párovém uspořádání sledujeme u téhož jedince (subjektu) binární proměnnou (ano/ne) dvakrát z nějakého důvodu, který vyplývá z experimentálního plánu. Například:
- sledování výskytu bolesti před operací a po ní, vždy u téhož pacienta,
- sledování výskytu nežádoucích účinků při léčbě X a při léčbě Y, opět u stejného pacienta, kde léčba Y následuje po léčbě X,
- sledování četnosti pozitivního výsledku u dvou laboratorních metod (např. záchyt infekčního agens ve vzorcích krve) při měření na stejné sadě vzorků,
- obecně sledování výskytu nějakého jevu před pokusem a po něm.
Hlavním cílem párového testu je zjistit, zda došlo ke změně výskytu daného znaku. Výstupem měření je opět jednoduchá tabulka četností 2 × 2. Při sledování párových dichotomických proměnných ji zapisujeme způsobem, který obecně uvádí tab. 2. Při párovém uspořádání ale nelze provést χ2 test, neboť pozorování zaznamenaná v tabulce četností nejsou nezávislá. Sledujeme v podstatě rozdíl ve výskytu daného znaku (pozitivita testu, výskyt bolesti) mezi dvěma vzájemně provázanými měřeními. Využijeme-li zápis v tab. 2 jako příklad, pak nás logicky zajímají pouze četnosti b, c, které jedině rozhodují o rozdílu mezi měřeními. Testujeme tedy, zda rozdíl v četnostech b, c mezi měřeními je náhodný, nebo zda je statisticky významný, což signalizuje změnu výskytu znaku. Klasickým postupem je zde McNemarův test, jehož výpočet přibližuje příklad 2. Tento test řadíme mezi neparametrické metody a jeho výpočet lze aplikovat pouze na tabulky o velikosti 2 × 2. Hovoříme o testování rozdílů u párově sbíraných nominálních dat.
Tab. 2. Tabulka četností dvou párově sledovaných binárních proměnných nabývajících hodnot 1/0. 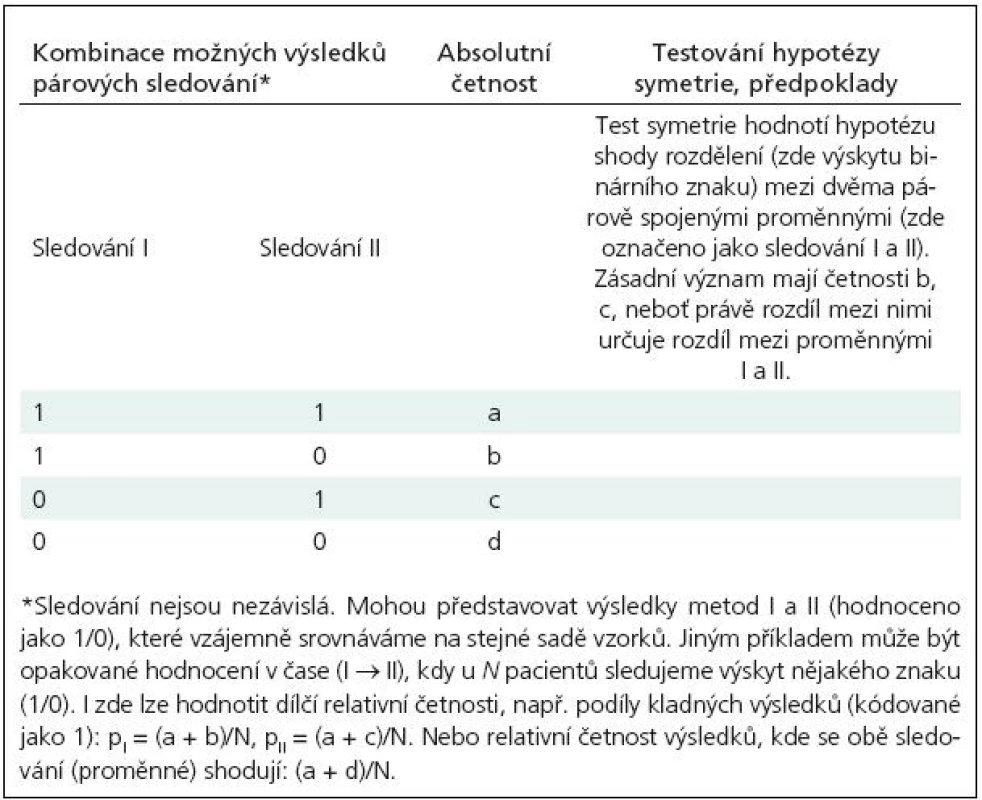
Příklad 2. McNemarův test pro párové srovnání dichotomických proměnných. 
Rozšířením McNemarova testu pro více než dva závislé výběry při sledování binární proměnné je tzv. Cochranův test (neboli Q-test dle Cochrana). Jde o neparametrické zobecnění McNemarova testu, kde sledovanou binární proměnnou třídíme podle více vzájemně nějak závislých kritérií (skupin) a sledujeme, zda se výskyt sledovaného znaku mění. Tak jako u McNemarova testu je sledovaná proměnná vždy binární (ano/ne). Příkladem využití mohou být tyto experimentální situace:
- srovnáváme výskyt pozitivního výsledku u více laboratorních metod a testujeme je závisle vždy na stejném vzorku; máme tedy N opakování (vzorků) a hypotézou je shoda mezi k metodami, kde k > 2,
- sledujeme výskyt určitého jevu (bolesti, nežádoucího účinku) u stejných pacientů opakovaně v čase; experiment o N opakováních (pacienti) srovnávající výskyt bolesti v k opakovaných měřeních, opět k > 2,
- sledujeme výskyt nějaké reakce v chování pokusných zvířat, která postupně podrobujeme různým pokusným zásahům; zde je počet opakování dán počtem zvířat v experimentu, srovnáváme různé pokusné zásahy.
Vždy se tedy jedná o situaci, kdy je jedinec (subjekt) vícenásobně sledován a je hodnocen výskyt určitého znaku. Provedená pozorování opět nejsou nezávislá a nelze je hodnotit χ2 testem. Výpočet Cochranova testu je uveden v příkladu 3.
Příklad 3. Cochranův Q test pro srovnání dichotomických proměnných ve více než dvou závislých pokusných variantách. 
Tak jako u mnoha jiných statistických testů sahá původ těchto metod hluboko do minulého století. Nicméně jde o výpočty stále platné a hojně využívané. Quinn McNemar (1900–1986) byl profesorem psychologie a statistiky univerzity ve Stanfordu a test publikoval v časopise Psychometrika v roce 1947. Tento test patří k jeho nejvýznamnějším dílům, mimo jiné také výrazně přispěl k revizi a vývoji testů IQ. Cochranův Q test je pojmenován po významném skotském statistikovi Williamu G. Cochranovi (1909–1980).
Tento díl seriálu opět zakončíme již téměř tradičním mentorováním o roli člověka ve věku počítačů. Je totiž zřejmé, že na numericky stejných datech (tabulka četností) lze bez problémů současně provést rozdílné testy, které ale hodnotí zcela rozdílné situace a vyžadují specifickou interpretaci výsledku. Hodnocení nezávislosti výskytu znaků nelze zaměnit za zkoumání změn ve výskytu znaku po určitém podnětu. Nicméně ale, když do statistických programů vložíme tabulku četností, například 2 × 2, nabídne nám menu všechny zde probrané testy naráz. Počítač nepřemýšlí, pouze koná. Je na experimentátorovi, lékaři, aby si uvědomil, co testuje a adekvátně zvolil vhodný test. Snad tomu náš seriál aspoň trochu napomáhá :-).
doc. RNDr. Ladislav Dušek, Dr.
Institut biostatistiky a analýz
Masarykova univerzita, Brno
e-mail: dusek@cba.muni.cz
Zdroje
Fleiss JL. Statistical methods for rates and proportions. 2nd ed. New York: John Wiley 1981.
McNemar Q. Note on the sampling error of the difference between correlated proportions or percentages. Psychometrika 1947; 12(2): 153–157.
Štítky
Detská neurológia Neurochirurgia Neurológia
Článok vyšiel v časopiseČeská a slovenská neurologie a neurochirurgie
Najčítanejšie tento týždeň
2010 Číslo 5- Metamizol jako analgetikum první volby: kdy, pro koho, jak a proč?
- Kombinace metamizol/paracetamol v léčbě pooperační bolesti u zákroků v rámci jednodenní chirurgie
- Neuromultivit v terapii neuropatií, neuritid a neuralgií u dospělých pacientů
- Antidepresivní efekt kombinovaného analgetika tramadolu s paracetamolem
- CIDP: epidemiológia, klinický obraz a diagnostika v kocke
-
Všetky články tohto čísla
- Antikoagulační terapie v prevenci a léčbě ischemických iktů
- Vývoj technik PLIF a TLIF
- Cievna mozgová príhoda a ischemická choroba srdca
- Konkomitantní chemoradioterapie a cílená biologická léčba u glioblastoma multiforme
- Syndrom útlaku ulnárního nervu v oblasti lokte – přehled operačních technik a srovnání jejich výsledků
- Analýza „default mode“ sítě u zdravých dobrovolníků
- Úloha predoperačného časového intervalu pri liečbe diskogenného syndrómu caudae equinae
- Výskyt psychogénnych porúch v neurológii
- Behaviorálne poruchy u pacientov s Parkinsonovou chorobou – anamnestický skríning za pomoci špecializovaného dotazníka
- Přítomnost tzv. typických MR nálezů u multisystémové atrofie a progresivní supranukleární paralýzy – retrospektivní pilotní studie
- Endoskopická transnazální chirurgie hypofýzy – výhody spolupráce otorinolaryngologa a neurochirurga
- Komentář k práci Matoušek et al Endoskopická transnazální chirurgie hypofýzy – výhody spolupráce otorinolaryngologa a neurochirurga
- Střelná poranění hlavy a mozku
- Hemangioblastom kaudy – kazuistika
- Neuralgie nervus pudendalis – kazuistika
- Bodná poranění míchy a míšních kořenů – kazuistiky
- Morbus Lhermitte-Duclos – kazuistika
- Aspekty tvorby klinických doporučených postupů v oboru neurologie podle národní metodiky
- Vývoj Národní sady klinických standardů a ukazatelů zdravotní péče a první výsledky v oboru neurologie
- Standard pro léčbu pacientů s autoimunitními nervosvalovými onemocněními intravenózním lidským imunoglobulinem a plazmaferézou
- Webové okénko
-
Analýza dat v neurologii XXIII.
Kontingenční tabulky neslouží jen pro testy hypotézy o nezávislosti znaků - Týden světové neurochirurgie v Praze – zpráva z kongresu
-
6. olomoucké neuroimunologické sympozium s mezinárodní účastí
16.–17. září 2010, Konvikt – Umělecké centrum Univerzity Palackého v Olomouci
- Česká a slovenská neurologie a neurochirurgie
- Archív čísel
- Aktuálne číslo
- Informácie o časopise
Najčítanejšie v tomto čísle- Neuralgie nervus pudendalis – kazuistika
- Vývoj technik PLIF a TLIF
- Syndrom útlaku ulnárního nervu v oblasti lokte – přehled operačních technik a srovnání jejich výsledků
- Střelná poranění hlavy a mozku
Prihlásenie#ADS_BOTTOM_SCRIPTS#Zabudnuté hesloZadajte e-mailovú adresu, s ktorou ste vytvárali účet. Budú Vám na ňu zasielané informácie k nastaveniu nového hesla.
- Časopisy



