-
Články
- Časopisy
- Kurzy
- Témy
- Kongresy
- Videa
- Podcasty
Analýza dat v neurologii: XXXVI. Hodnocení statistické významnosti poměru šancí a relativního rizika
Autori: L. Dušek; T. Pavlík; Jiří Jarkovský
; J. Koptíková
Pôsobisko autorov: Institut biostatistiky a analýz MU, Brno
Vyšlo v časopise: Cesk Slov Neurol N 2012; 75/108(6): 764-767
Kategória: Okénko statistika
V minulém díle seriálu jsme otevřeli velmi frekventované téma hodnocení těsnosti vztahu (asociace) mezi expozicí osob nějakému faktoru a výskytem studované rizikové události (vznik nemoci, relaps nemoci, úmrtí…). V tomto a dalších pokračováních seriálu se zaměříme na správnou interpretaci výsledku těchto analýz. V příkladech minulého dílu jsme probírali specifika asociačních analýz u různých typů observačních (neintervenčních) studií, které jsme za tímto účelem rozdělili na prospektivní (kohortové), retrospektivní (studie případů a kontrol) a průřezové. Toto členění a odhady poměru šancí („odds ratio“, OR) a relativního rizika („relative risk“, RR) se k hodnocení vztahu různých jevů standardně využívají i v klinickém výzkumu, přičemž musíme respektovat zásadní pravidla, rovněž vysvětlená v XXXV. díle seriálu:
- RR lze využít pouze u prospektivních a průřezových studií, kde je výběr jedinců náhodný z hlediska výskytu sledované události; výskyt události zde sledujeme reprezentativně v čase.
- OR má své uplatnění naopak především u retrospektivních studií, i když jej lze odhadnout i u prospektivních nebo průřezových pozorování; jelikož u retrospektivních studií přímo zařazujeme osoby dle výskytu události, nelze výskyt události považovat za náhodný a reprezentativní – tyto studie směřují pouze k hodnocení vztahu mezi expozicí a výskytem události, neumožňují odhad populační incidence a prevalence sledované události.
V nejjednodušším případě je výstupem těchto pozorování 2 × 2 tabulka četností, ve které zaznamenáváme absolutní četnosti toho, kolikrát nastaly možné kombinace „expozice faktorem (ano/ne) vs událost (ano/ne), např. diabetes mellitus vs výskyt centrální mozkové příhody. Výpočet a rozdílnou interpretaci OR a RR přibližuje obr. 1. Je patrné, že způsob výpočtu relativního rizika předpokládá reprezentativní výskyt sledované události v hodnocené populaci, neboť odhadujeme její relativní výskyt ve skupině exponované, a dělíme jej relativním výskytem události ve skupině bez expozice. Pokud by výskyt událostí v daném vzorku pacientů nebyl náhodný a reprezentativní, byl by odhad RR zkreslen. Naopak výpočet poměru šancí odhaduje šanci výskytu události v rámci exponované skupiny a tu dělí šancí výskytu události v rámci skupiny neexponované. Rozdíl mezi odhadem OR a RR je tedy zásadní a oba statistické ukazatele nelze zaměňovat.
Zde se hodí připomenout, proč jsou asociační studie v medicíně tak často využívany a co je jejich hlavním cílem. Tato pozorování slouží zejména k:
- identifikaci rizikových nebo protektivních faktorů, které ovlivňují výskyt nějaké klinicky významné události (komplikace léčby, recidivy nemoci, smrt); v epidemiologii takto studujeme i faktory ovlivňující samotný vznik, a tedy incidenci nemoci,
- posouzení a kvantifikaci těsnosti těchto vztahů a seřazení faktorů podle významu (síly) jejich vlivu,
- srovnání vlivu různých faktorů ovlivňujících výskyt sledované události mezi různými skupinami (kohortami) pacientů a kontrolních osob.
Je zřejmé, že odhady poměru šancí a relativního rizika směřují ke klinicky velmi závažným interpretacím. V dalším výkladu se zaměříme především na opatření, která pojistí dosažení věcně správného, nezkresleného výsledku těchto analýz. To je v první řadě schopnost rozpoznat statisticky významnou hodnotu poměru šancí, resp. relativního rizika, a tyto hodnoty mezi sebou relevantně srovnat. U srovnávacích analýz potom musíme dbát i na věcnou srovnatelnost různých skupin pacientů a kontrol, jinak i dobře provedený výpočet povede k chybnému závěru.
Hodnocení statistické významnosti výsledku u jednoduchých asociačních studií není nijak složité. Nejjednodušší způsob, jak vyhodnotit význam odhadu poměru šancí i relativního rizika, je posouzení jejich intervalu spolehlivosti, přičemž podobně jako u jiných statistik se i zde standardně využívá 95% interval. Každý odhad OR nebo RR by měl být publikován se svým intervalem spolehlivosti, neboť bez něj nemůže být interpretace těchto ukazatelů plnohodnotná. Výpočet intervalu spolehlivosti pro odhad OR a RR dokumentují příklady 1 a 2, které pracují s různými soubory dat a nabízejí rozdílné výsledky. Interpretace je nicméně velmi jednoduchá. Pokud interval spolehlivosti zahrnuje hodnotu 1, nemůžeme daný odhad OR či RR považovat za statisticky významný. Hodnota OR = 1 nebo RR = 1 totiž označuje situaci, kdy sledovaný faktor (expozice) neovlivňuje výskyt dané události; jde tedy o referenční hodnotu („no effect“). Pokud tedy interval spolehlivosti zahrnuje hodnotu 1, pak nelze prokázat statisticky významný rozdíl ve výskytu události mezi exponovanými a neexponovanými jedinci. Za těchto okolností jednoduše nemůžeme vyloučit, že rozdíl odhadnuté hodnoty OR (RR) od 1 je důsledkem náhodných výchylek a variability v měření.
Pokud je bodový odhad OR > 1 nebo RR > 1 a korespondující interval spolehlivosti nezahrnuje hodnotu 1, je takto identifikován statisticky významný rizikový faktor (při 95% intervalu spolehlivosti hovoříme o 5% hladině významnosti). Obdobně hodnoty OR < 1 nebo RR < 1 s horní hranicí intervalu spolehlivosti pod 1 identifikují statisticky významný protektivní faktor.
Jistou zvláštností intervalů spolehlivosti pro OR nebo RR, například ve srovnání s intervalovými odhady pro průměr jako odhad střední hodnoty, je jejich asymetrie. Výpočty doložené v příkladech 1 a 2 pracují s aproximací pomocí normálního rozdělení pro hodnoty ln(OR) a ln(RR). Po odlogaritmování (exponenciální funkcí) tak vždy nutně získáváme asymetrické hranice intervalů. Výpočty s pomocí aproximace na normální rozdělení jsou zjednodušením, které nám umožňuje snadný výpočet intervalů spolehlivosti. Konkrétně tento postup předpokládá, že logaritmus OR (tzv. Woolfova metoda) nebo logaritmus RR (tzv. Katzova metoda) mají přibližně normální rozdělení. Tento předpoklad platí ale jen u dostatečně velkých souborů dat, proto by se tyto postupy neměly využívat u malých souborů. Jejich nesprávná aplikace může paradoxně vést k velmi úzkým intervalům spolehlivosti, které neodpovídají reálné skutečnosti. Neplatí totiž, že užší interval spolehlivosti znamená vždy lepší výsledek a lepší odhad OR nebo RR. Rovněž by byla velká chyba vybírat metodu odhadu intervalu spolehlivosti pokusně podle jeho výsledné šířky. U malých souborů dat jsou obecně doporučeny metody exaktních odhadů nebo iterační postupy, pro které je nutné využít specializované počítačové programy z důvodů výpočetní náročnosti. U odhadů OR lze v menu statistických programů nalézt tzv. Cornfieldovy meze spolehlivosti (podle Cornfieldovy metody výpočtu intervalu spolehlivosti), které jsou poměrně přesnou aproximací i u malých souborů dat. Jelikož tedy aproximace na normální rozdělení představená v příkladech 1 a 2 není univerzálně využitelná, doporučujeme uživatelům statistických programů konzultovat výběr vhodné metody s odborníkem na statistiku, a to zejména u souborů malého rozsahu, kde přesnost odhadu intervalu spolehlivosti závisí i na tom, jak moc je hodnota OR (RR) vzdálena od hodnoty 1.
Obr. 1. Grafické srovnání výpočtu relativního rizika (<em>RR</em>) a poměru šancí (<em>OR</em>). 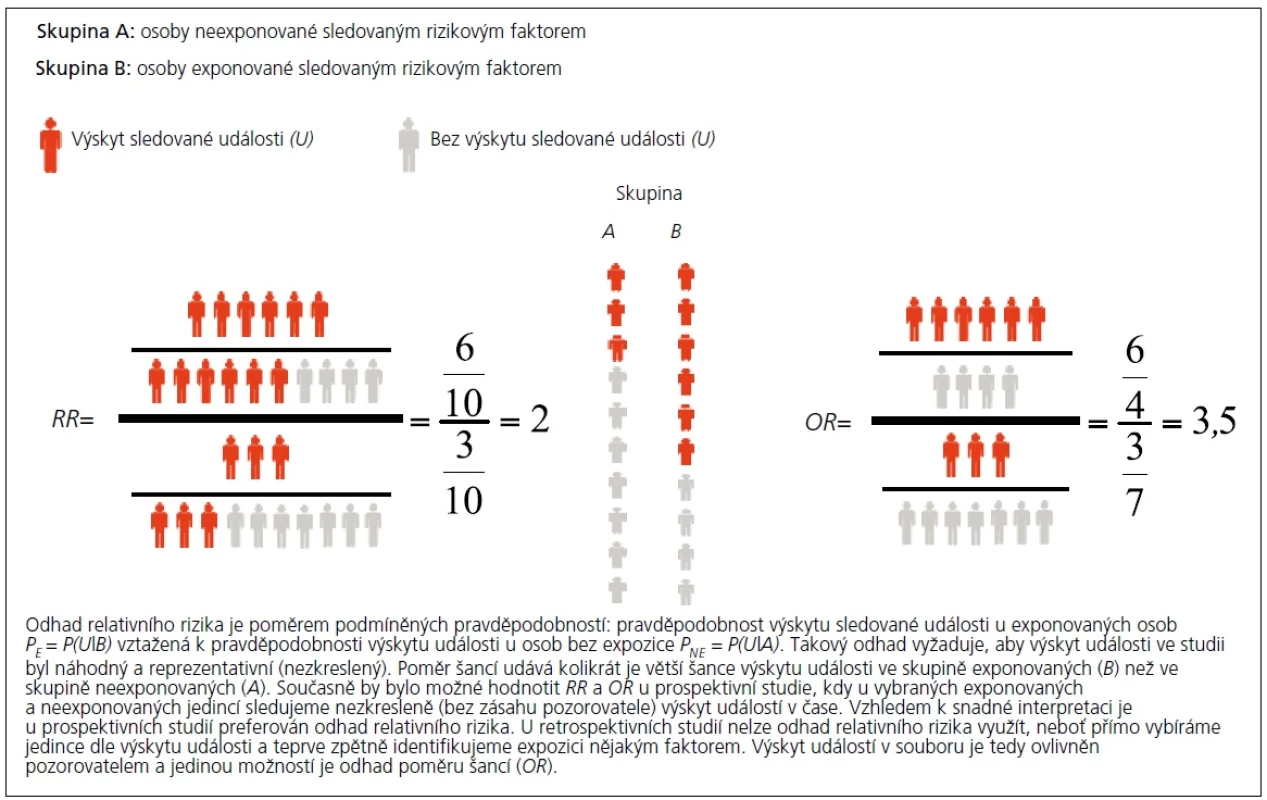
Po přečtení předchozího odstavce čtenáře jistě napadne otázka, jaký je tedy skutečně správný postup při posuzování významnosti asociace náhodných veličin v tabulce četností. A může vůbec uživatel-nematematik posoudit statistickou významnost poměru šancí nebo relativního rizika? Odpověď je naštěstí pozitivní a správný postup lze stručně popsat v následujících krocích:
- Zvážíme uspořádání (design) a typ hodnocené studie (retrospektivní, průřezová, prospektivní) a rozhodneme se pro odhad odpovídajícího ukazatele asociace (poměr šancí nebo relativní riziko).
- Provedeme statistický test nulové hypotézy o nezávislosti veličin v kontingenční tabulce (Pearsonův chí-kvadrát test nebo Fisherův exaktní test) jako obecný test potvrzující nebo vyvracející hypotézu o nezávislosti zkoumaných veličin.
- Vypočítáme odhad OR nebo RR a doplníme jej intervalem spolehlivosti (standardem je 95% interval); pokud je analyzovaný soubor dostatečně velký a v každém políčku tabulky je absolutní četnost minimálně 5, pak lze aplikovat i jednoduchý postup vycházející z aproximace na normální rozdělení (viz příklady 1 a 2).
- Výstup testu a výpočet intervalu spolehlivosti provedené v bodech 2 a 3 se v naprosté většině případů vzájemně potvrzují. Tedy statisticky významný výstup testu v bodě 2 potvrzuje obecně existenci vztahu zkoumaných veličin a potom intervaly spolehlivosti pro OR nebo RR nezahrnují hodnotu 1. A naopak, pokud obecnými testy prokážeme nezávislost veličin (bod 2), pak ani OR, resp. RR, neposkytnou průkazné výstupy. Rozdíly mezi těmito postupy sice nastat mohou, ale pouze v hraničních situacích, kdy se může projevit např. chyba aproximativních výpočtů (příklad 2).
Příklad 1. Hodnocení výstupů průřezové studie sledující vztah mezi podprůměrnou porodní váhou chlapců a výskytem nádoru varlat do 25 let věku – příklad s jednoznačným výsledkem. 
Příklad 2. Hodnocení výstupů průřezové studie sledující vztah mezi podprůměrnou porodní váhou chlapců a výskytem nádoru varlat do 25 let věku – příklad s nejednoznačným výsledkem. 
Doporučený postup hodnocení se tedy skládá ze dvou vzájemně komplementárních výpočtů. Statistické testy nezávislosti dvou veličin vedou ke standardnímu výstupu ve formě statistické p-hodnoty („p value“). Čím nižší hodnotu p obdržíme, tím menší je pravděpodobnost pozorovaného výsledku při platnosti nulové hypotézy (zde H0 odpovídá nezávislosti obou veličin), a tím pravděpodobnější je hypotéza alternativní, tedy že veličiny jsou vzájemně závislé. Například při výsledku Fisherova exaktního testu p = 0,013 zamítáme nulovou hypotézu a obě veličiny označujeme za vzájemně závislé. Avšak tento test nevyjadřuje sílu hodnoceného vztahu a rovněž neurčuje věcnou, zde např. klinickou významnost prokázaného vztahu. Proto odpovídající odhad OR nebo RR (bod 3 výše uvedeného postupu) doplní statisticky prokázanou závislost veličin jako kvantitativní míra síly tohoto vztahu. Lze očekávat, že interval spolehlivosti OR (RR) za této situace nezahrnuje hodnotu 1.
Učebnicová interpretace 95% intervalu spolehlivosti říká, že budeme-li 100krát nezávisle opakovat odhad OR nebo RR na výběrovém souboru stejné velikosti, minimálně 95 % výsledků bude ležet v hranicích vymezených intervalem. Je tak vymezen interval, v němž leží s 95% pravděpodobností skutečná populační hodnota OR nebo RR. Výše jsme doložili, že interval spolehlivosti pro OR nebo RR lze rovněž využít jako indikátor vztahu dvou veličin na určité hladině významnosti. Jeho šířka však rovněž ukazuje na přesnost provedeného odhadu a souvisí i s velikostí analyzovaného souboru. Shoda závěrů vyplývajících z intervalů spolehlivosti a ze statistických testů nezávislosti dvou veličin (body 2–3 výše uvedeného postupu) tak nemusí vždy nastat. Například je možné, že obecným testem prokážeme závislost, nicméně interval spolehlivosti pro OR nebo RR bude velmi široký a může dokonce i zahrnout hodnotu 1. V takovém případě je nutná velká opatrnost při interpretaci zjištěné závislosti.
Doufejme, že se nám přiloženými příklady povedlo popsat prakticky využitelné postupy pro hodnocení významnosti odhadů poměru šancí nebo relativního rizika. Aproximativní postupy ukázané v příkladech 1 a 2 mají jedinou podmínku, a sice vyžadují dostatečnou velikost vzorku. Jinak jsou jednoduché a lze je provést i bez specializovaného SW. Avšak pomocí dostupných statistických programů lze snadno aplikovat jinou metodu pro výpočet intervalů spolehlivosti pro OR nebo RR. Z tohoto pohledu je dnešní doba velmi vstřícná, rozvoj počítačové techniky umožňuje provádět sofistikované analýzy i laickým uživatelům zmíněných SW nástrojů. Nikdy však nesmíme zapomenout, že ani sebelepší SW a metoda výpočtu z nás nesnímá odpovědnost za rozhodnutí, zda v dané situaci využít OR nebo RR, a také odpovědnost za interpretaci výsledku. Statisticky významný výsledek testu prokazující závislost dvou jevů ve vzorku N osob neznamená, že ta na 100 % existuje i v cílové populaci, a rovněž nic nevypovídá o jejím klinickém významu. Z jednoduchých tabulek četností 2 × 2 také nevyčteme a nezdůvodníme kauzální vztahy mezi veličinami a násilná interpretace výsledků může vést k zcela chybným, až paradoxním závěrům. Jak rozpoznávat rizika zkreslení a jak jim předcházet, se pokusíme přiblížit v dalším díle seriálu.
doc. RNDr. Ladislav Dušek, Dr.
Institut biostatistiky a analýz
MU, Brno
e-mail: dusek@cba.muni.cz
Štítky
Detská neurológia Neurochirurgia Neurológia
Článek Kortikální patologie u roztroušené sklerózy – morfologické, imunopatologické a klinické souvislostiČlánek CENS Praha 2012Článek Prediktory symptomatického intracerebrálního krvácení po systémové trombolýze mozkového infarktuČlánek Rekurentní analýza variability srdeční frekvence v časné diagnostice diabetické autonomní neuropatieČlánek Měření atrofie corpus callosum a porovnání s ostatními metodami monitorace roztroušené sklerózyČlánek Kongenitální myastenie jako příčina respiračního selhání u dvou kojenců a batolete – kazuistikyČlánek Webové okénkoČlánek Pít, či nepít?Článek Spinální kongres
Článok vyšiel v časopiseČeská a slovenská neurologie a neurochirurgie
Najčítanejšie tento týždeň
2012 Číslo 6- Metamizol jako analgetikum první volby: kdy, pro koho, jak a proč?
- Kombinace metamizol/paracetamol v léčbě pooperační bolesti u zákroků v rámci jednodenní chirurgie
- Neuromultivit v terapii neuropatií, neuritid a neuralgií u dospělých pacientů
- Antidepresivní efekt kombinovaného analgetika tramadolu s paracetamolem
- CIDP: epidemiológia, klinický obraz a diagnostika v kocke
-
Všetky články tohto čísla
- Endovaskulární léčba ischemické cévní mozkové příhody
- Kortikální patologie u roztroušené sklerózy – morfologické, imunopatologické a klinické souvislosti
- Fázový model neurorehabilitace
- Vztah vaskulárních rizikových faktorů a Alzheimerovy choroby
- Epidemie roztroušené sklerózy ve světě?
- Laboratorní preparace drah z mediálního pohledu na mozkovou hemisféru
- Prediktory symptomatického intracerebrálního krvácení po systémové trombolýze mozkového infarktu
- Rekurentní analýza variability srdeční frekvence v časné diagnostice diabetické autonomní neuropatie
- Molekulárně genetická analýza tkáně plodu rodiny postižené myotonickou dystrofií
- Opakovaná víceetážová aplikace botulinum toxinu A dlouhodobě zabraňuje zhoršení chůze u dětí s dětskou mozkovou obrnou
- Měření atrofie corpus callosum a porovnání s ostatními metodami monitorace roztroušené sklerózy
- Výskyt epileptického záchvatu pri intraoperatívnej stimulácii mozgu – naše skúsenosti
- Papilární nádor pineální oblasti u dítěte – kazuistika
- Kongenitální myastenie jako příčina respiračního selhání u dvou kojenců a batolete – kazuistiky
- Webové okénko
- Analýza dat v neurologii: XXXVI. Hodnocení statistické významnosti poměru šancí a relativního rizika
- CENS Praha 2012
- Prof. MUDr. Zdeněk Lukáš, CSc. (1934–2012)
- Pít, či nepít?
- Spinální kongres
- Česká a slovenská neurologie a neurochirurgie
- Archív čísel
- Aktuálne číslo
- Informácie o časopise
Najčítanejšie v tomto čísle- Epidemie roztroušené sklerózy ve světě?
- Spinální kongres
- Kortikální patologie u roztroušené sklerózy – morfologické, imunopatologické a klinické souvislosti
- Fázový model neurorehabilitace
Prihlásenie#ADS_BOTTOM_SCRIPTS#Zabudnuté hesloZadajte e-mailovú adresu, s ktorou ste vytvárali účet. Budú Vám na ňu zasielané informácie k nastaveniu nového hesla.
- Časopisy



