Analýza dat v neurologii
XLVI. Různé typy observačních studií nesou různá rizika zkreslení
Autori:
L. Dušek; T. Pavlík; J. Jarkovský
; J. Koptíková
Pôsobisko autorov:
Masarykova univerzita, Brno
; Institut biostatistiky a analýz
Vyšlo v časopise:
Cesk Slov Neurol N 2014; 77/110(4): 519-523
Kategória:
Okénko statistika
V dílech XXXIX– XL seriálu jsme se zabývali hodnocením vlivu zavádějících faktorů na odhad míry vztahu dvou náhodných veličin (asociační studie expozice vs účinek). V podstatě šlo o výklad různých korekčních postupů („adjustace“) prováděných již po získání konečného souboru dat s cílem zabránit zkreslení výsledku. V dílech XL–XLV jsme doložili, že nekontrolované zastoupení vlivného zavádějícího faktoru ve srovnávaných skupinách může zcela znehodnotit prováděný výzkum, jeho hodnocení a interpretaci. Pozorné čtenáře jistě napadlo, proč se tolik věnujeme zpětné korekci výsledků asociačních studií, když daleko účinnější musí být kontrola možného zkreslení již při samotném plánování studie a náběru probandů. Tato úvaha je správná, neboť dodržováním zásad správných metodických postupů můžeme riziko zkreslení minimalizovat, byť zcela eliminovat jej nelze. Klíčem k úspěchu je zvolit správný experimentální plán, správnou metodu zařazování probandů, dále dbát na reprezentativnost vzorku vzhledem k cílové populaci a správně pracovat s prevalencí hodnoceného znaku (události) v cílové populaci. Všechny tyto faktory zásadně ovlivňují interpretaci výsledků. Samozřejmě ne vždy se podaří realizovat studii s vyloučením všech potenciálních hrozeb zkreslení, avšak pokud tato fakta zohledníme při interpretaci výsledků, je to jistě korektní. Předem totiž nemůžeme zajistit nulové riziko zkreslení u žádného typu studie.
Design observačních studií a jeho dopad na analýzu vztahu „expozice‑účinek“
Univerzální pravidlo, které by k různým typům zkoumaných problémů přiřadilo nejlepší možný typ studie, bohužel neexistuje. Prospektivní i retrospektivní experimentální plány mají své výhody i negativa. Obecně platí, že u retrospektivního sběru dat lze kontrolovat menší počet zavádějících faktorů a celkově jsou tyto plány náchylnější ke zkreslení výsledků.
Nekontrolovaný vliv zavádějících faktorů nebo nesprávné podchycení expozice a jejího účinku se promítá do tzv. observačního zkreslení („observation bias“, „information bias“). Nicméně zde máme k dispozici poměrně silné nástroje, jak zkreslení předejít, např. vyváženým strukturováním souborů případů a kontrol („matched case – control design“). Jako nástroj zajišťující co největší srovnatelnost skupin se vyvážený design ovšem uplatňuje i u ostatních experimentálních plánů, včetně prospektivních kohortových studií.
Kromě vyváženého designu studie patří mezi hlavní atributy, které je nutno kontrolovat, metodika vzorkování a reprezentativnost vzorku. Pokud je náběr probandů realizován odlišně pro exponovanou a kontrolní skupinu, může dojít k tzv. výběrovému zkreslení („sampling bias“, „selection bias“). O všech těchto pochybeních hovoříme jako o systematické chybě či zkreslení a jde samozřejmě o velmi vážný problém ovlivňující samotnou podstatu výzkumu. Je samozřejmé, že pokud je již samotný náběr populačního vzorku chybný a zkreslený, pak výsledky výzkumu nezachrání žádná statistická technika.
V následujícím výkladu se budeme věnovat záchytu sledované události (účinku expozice) a reprezentativnosti vzorku a rozebereme jejich vliv na výsledný odhad poměru šancí a relativního rizika. Jde o téma zásadní, vzorkování v různých populacích lišících se prevalencí sledované události často vede k obtížně srovnatelným výsledkům. Nadto sama četnost sledované události ovlivňuje výsledky hodnocení asociačních (kontingenčních) tabulek četností, neboť určuje počty pozorování, kterých můžeme dosáhnout v jednotlivých buňkách tabulky.
Vliv experimentálního plánu na výsledky asociační studie nejlépe vysvětlíme, když si připomeneme způsob výpočtu poměru šancí a relativního rizika. Vraťme se k nejjednoduššímu typu asociační studie, kterou lze shrnout pomocí čtyřpolní tabulky četností, jejíž políčka standardně označujeme písmeny a až d (tab. 1). Typickým výstupem tabulky je výpočet relativního rizika a poměru šancí.

Oba ukazatele míry asociace lze samozřejmě spočítat současně na jakékoli tabulce četností 2 × 2. Relativní riziko má ale interpretační smysl pouze u prospektivních studií (typickým příkladem jsou kohortové studie), na jejichž počátku známe pouze exponovanou a neexponovanou skupinu a na výskyt události v obou skupinách následně „čekáme“. U retrospektivních sledování již na počátku studie vybíráme osoby s událostí a bez ní, a tudíž přímo rozhodujeme o hodnotách relativní četnosti (a + b)/(a + b + c + d). A tedy odhady pravděpodobnosti výskytu události v exponované skupině, a/(a + c), a kontrolní skupině, b/(b + d), nelze považovat za produkt náhodného vzorkování. V takovém případě hodnota RR nemá relevantní interpretační smysl. Avšak poměr šancí OR není vlivem vzorkování a designu studie dotčen a je možné jej využít u retrospektivních i u prospektivních experimentálních plánů. Obecně ale platí, že u prospektivních studií preferujeme odhad RR, neboť má větší informační hodnotu; zahrnuje i odhad pravděpodobnosti výskytu události pod vlivem expozice a bez ní.
Vliv vzorkování a prevalence znaku u prospektivních studií
Ačkoli jsou prospektivní studie v literatuře více ceněny než retrospektivní plány, vliv vzorkování na interpretaci výsledků se nevyhýbá ani jim. Vzorkování vždy ovlivní relativní záchyt sledovaného jevu v exponované i v kontrolní skupině. Ideální stav je ovšem jasný, prevalence znaku v kontrolním rameni studie by měla odpovídat prevalenci v reálné populaci. Pokud tohoto stavu nejsme z řady praktických důvodů schopni dosáhnout, je třeba na kontrolní skupinu nahlížet jen jako na účelově získanou kohortu určenou k srovnání s kohortou exponovanou. V této situaci se velmi často využívá odhadu tzv. atributivního rizika, které vyjadřuje přímý vliv expozice studovaným faktorem na výskyt události a kalkuluje se jako rozdíl ve výskytu sledovaného jevu ve skupině ovlivněné faktorem a ve skupině bez tohoto ovlivnění. Takto získaná data lze však interpretovat pouze jako experimentálně odhadnutý vliv expozice, nikoli jako odhad reálné prevalence studovaných jevů.
Je zřejmé, že prospektivní design studie není synonymem pro reprezentativní odhad prevalence (reálného výskytu) znaku/ jevu v populaci. Velmi často zde studujeme sice prospektivně a náhodně výskyt jevu v čase, avšak v účelově nabraných kohortách, které neumožňují populační zobecnění odhadnutých prevalencí. Naměřená prevalence znaku v kontrolní skupině nadto nemá vliv jen na samotnou interpretaci výsledků. Prevalence znaku ovlivňuje i samotnou hodnotu relativního rizika. Právě z tohoto důvodu bývají odhady RR generované z populací s různou prevalencí znaku obtížně srovnatelné. Při výpočtu hodnoty RR (tab. 1) totiž přímo kalkulujeme poměry a/(a + c), b/(b + d), a ty následně dáváme do vzájemného poměru. S rostoucí prevalencí znaku v kontrolní skupině narůstá hodnota poměru b/(b + d) a výsledná hodnota RR tak může být menší než u populace s méně prevalentním sledovaným znakem.
Vliv prevalence znaku na hodnotu RR přibližují příklady 1 a 2, které shrnují data z různých prospektivních studií. Jelikož u takových studií, na rozdíl od retrospektivních pozorování, je možné současně kalkulovat RR i OR, oba příklady nabízejí i srovnání hodnot těchto ukazatelů při různé prevalenci znaku v populaci. Z výsledků vyplývají dva hlavní závěry:
- hodnota OR je na prevalenci znaku v kontrolní populaci nezávislá, což OR favorizuje pro případ výpočtů z různých populací lišících se prevalencí zkoumaného jevu; prevalence znaku v populaci nicméně ovlivňuje variabilitu odhadu OR (viz příklad 2),
- při nízké prevalenci znaku v populaci je hodnota OR a RR číselně téměř totožná; hodnota RR začíná klesat, a tedy se odlišovat od hodnoty OR, až při cca 10% a vyšší prevalenci jevu v kontrolní populaci.


Numerickou shodu odhadů OR a RR při zkoumání vzácných jevů (jevů s nízkou prevalencí v kontrolní populaci) lze poměrně snadno vysvětlit. Využijeme k tomu ukázku výpočtů v tab. 1. Pokud je prevalence nemoci velmi nízká, pak platí a << c a zároveň b << d. Potom bude platit a ++ c ~ c, b + d ~ d, a hodnota RR se pak přibližně rovná hodnotě OR, jehož definiční vztah je (a/ c)/ (b/ d). S rostoucí prevalencí znaku v kontrolní skupině se hodnota RR více odlišuje od hodnoty OR a klesá.
Na závěr této části je nutné zdůraznit, že prevalence nemoci je populační charakteristika, která ovlivňuje výskyt nemoci, ale nebývá prospektivními studiemi přímo odhadována. U prospektivní studie „čekáme“ na výskyt nemoci v exponované a v kontrolní skupině v čase, a tedy fakticky zaznamenáváme incidenci onemocnění. Vztah mezi incidencí a prevalencí závisí na typu onemocnění, kdy incidence je čistě funkcí výskytu nových případů onemocnění za daný časový interval, zatímco prevalence je funkcí incidence (ta zvyšuje prevalenci onemocnění) a vyléčení onemocnění či úmrtí na onemocnění za daný čas (ty snižují prevalenci onemocnění). Mohou tak nastat jak situace, kdy onemocnění má vysokou incidenci, ale nízkou prevalenci (onemocnění je rychle léčitelné nebo má vysokou úmrtnost v krátkém čase), tak situace, kdy onemocnění má nízkou incidenci, ale vysokou prevalenci (typicky chronická onemocnění). Při interpretaci výsledků prospektivní studie vzhledem k prevalenci je tak třeba vždy zohlednit populační charakteristiky sledovaného onemocnění; i v takovém případě nicméně nejde o přímý odhad populační prevalence ze vzorku studie, ale pouze o výsledek modelu vztahu incidence a prevalence pro dané onemocnění. Okamžitou nebo intervalovou prevalenci nemoci odhadují především studie průřezové.
Vliv vzorkování a prevalence znaku u průřezových studií
Průřezové studie („cross-sectional trials“) představují typ pozorování se specifickým vzorkovacím plánem. Mohou být organizovány jako retrospektivní i prospektivní a bývají přímo zaměřeny na odhad prevalence znaku v populaci. Proto se jim také často říká studie prevalenční. Na rozdíl od již zmíněných retrospektivních a prospektivních plánů zde není uplatněno sledování v čase a tabulku četností získáme náhodným výběrem jedinců z cílové populace v jednom časovém okamžiku anebo ve velmi krátkém časovém intervalu, během kterého se zastoupení znaku v populaci (vztah „expozice‑ následek“) nemůže změnit. Podstatné je, že všechna pole čtyřpolní tabulky četností nabíráme ve stejném časovém okamžiku. Výsledek je potom nutné interpretovat ve vztahu k danému časovému bodu, protože je časově podmíněný.
Jelikož průřezové studie „nečekají“ na výskyt události či expozice v čase, nepracují s incidencí jevů jako např. prospektivní studie, ale přímo odhadují prevalenci. Pokud jsou všechna čtyři políčka tabulky četností (tab. 1) výsledkem průřezového náběru na základě náhodného vzorku, poskytuje tento postup velmi spolehlivý odhad okamžité prevalence nemoci v neexponované populaci (tab. 1: b/ (b + d)), okamžité celkové prevalence nemoci (tab. 1: (a + b)/ n) a také údaj o okamžité prevalenci exponovaných jedinců v populaci (tab. 1: (a + c)/ n). Pokud k hodnocení průřezové studie využijeme relativní riziko, jde zde vlastně o poměr odhadu prevalence nemoci v exponované skupině a prevalence nemoci v kontrolní skupině. Odhad relativního rizika tu bývá označován jako poměr prevalencí („prevalence ratio“).
Ani tento plán studie ale není ušetřen od možných zkreslení. Ta nastávají zejména u vzácných jevů (nemocí), kde získání náhodného vzorku o velikosti potřebné pro záchyt prevalence v průřezovém sledování není reálné. Průřezová sledování také nutně zkreslují odhady u jevů, které jsou silně časově proměnlivé, ať již jde o expozici fluktuující v čase nebo krátkodobá akutní onemocnění či onemocnění s vysokou krátkodobou mortalitou. Velkým interpretačním problémem průřezových studií je kauzalita zjištěných vztahů. Pokud nejde o expozici s jasnou historickou anamnézou u zkoumaných jedinců (např. úraz v minulosti, genetický znak apod.), lze často jen obtížně identifikovat expozici a její následek. V učebnicích se mnohdy uvádí příklad kuřáctví a psychiatrických poruch, kde kuřáctví může těmto chorobám předcházet, ale může být i jejich následkem. Průřezová studie v takové situaci sice identifikuje vztah, ale nemůže jej hodnotit ve smyslu příčina‑ následek. K tomu je následně nezbytné připravit prospektivní kohortovou studii nebo retrospektivní studii případů a kontrol.
Vliv vzorkování a prevalence znaku u retrospektivních studií
Představme si retrospektivní observační studii, kdy nabíráme kohortu s událostí (např. pacienty s určitou chorobou) s pravděpodobností P, z čehož vyplývá, že kohortu kontrolní získáváme s pravděpodobností (1 – P). Jde o retrospektivní studii, u které zpětně studujeme, zda osoby byly vystaveny sledované expozici (např. jsou‑li zařazené osoby nositelem určitého genetického znaku či prodělaly‑li v anamnéze určitý typ terapie, apod.). Doplňme v tomto smyslu výpočty relativních četností realizované expozice pro skupinu s událostí a bez události v políčkách tabulky 2 × 2 (tab. 2).
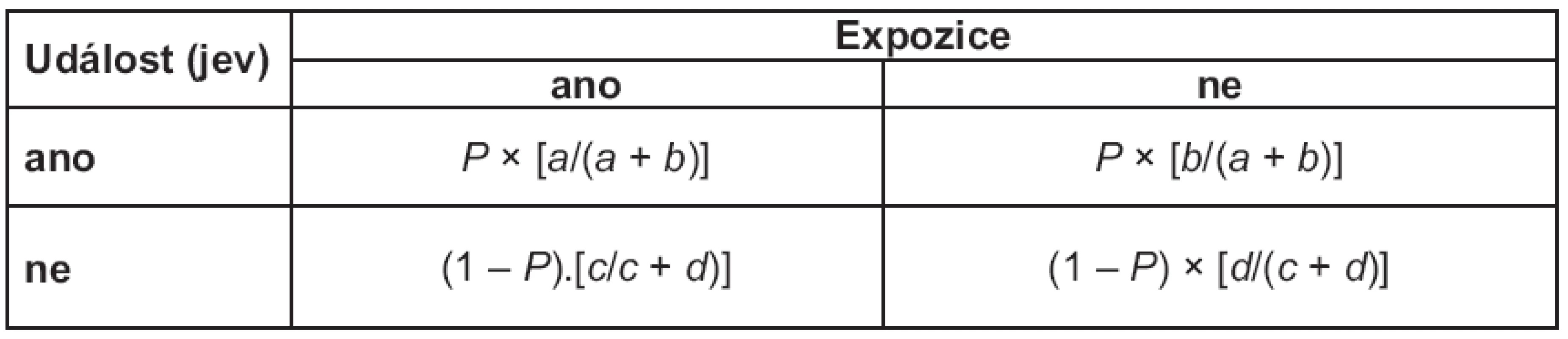
Je zřejmé, že hodnotu relativního rizika, které je poměrem odhadů pravděpodobnosti nastání události v exponované a kontrolní skupině, v podstatě nelze u retrospektivního designu smysluplně spočítat. Naopak odhad šance vzniku události v obou skupinách daných hodnotou expozice v takto nastaveném retrospektivním plánu ovlivněn není, tj. poměry a/ c i b/ d nejsou retrospektivním vzorkovacím plánem nijak dotčeny (resp. pravděpodobnost P se při výpočtu OR vykrátí).
Způsob náběru vzorku a jeho reprezentativnost je zásadní faktor určující hodnocení a interpretaci těchto studií. V ideálním případě bychom měli tabulku četností získat zcela náhodným výběrem z cílové populace, tedy získat tzv. populační vzorek. Potom by relativní četnosti v buňkách tabulky reprezentovaly zároveň odhad pravděpodobnosti výskytu daných jevů v cílové populaci a žádný zásah experimentátora, který určil pravděpodobnost P výběru skupin (tab. 2), by nenastal. Ačkoli má tento přístup jasné interpretační výhody, jeho naplnění není v praxi často reálně možné. Hlavními důvody jsou omezená dostupnost vzorku a nízká prevalence jevu v cílové populaci.
Například pokud studujeme vliv pracovní expozice azbestem na vznik zhoubných nádorů mezihrudí, jsme limitováni nízkou prevalencí těchto onkologických onemocnění. Jde o objektivní faktor, který nemůžeme nijak ovlivnit. Při zcela náhodném výběru bychom potřebovali nereálně velký vzorek celé populace, abychom data mohli vůbec vyhodnotit. Zvolíme‑li zde retrospektivní design studie, bude studie realizovatelná přes onkologická zdravotnická zařízení, kde získáme potřebnou kohortu pacientů s danými nádory relativně snadno. Zpětně potom zaznamenáváme, zda byly osoby v zaměstnání vystaveny vlivu azbestu či nikoli. Kontrolní vzorek osob bez daného nádoru nabereme paralelně („case‑ control design“) a můžeme jej strukturovat např. podle věku a pohlaví, aby byl co nejvíce srovnatelný s kohortou pacientů („matched case – control design“). Je zřejmé, že podíl onkologických pacientů v získané tabulce četností neodráží jejich reálný výskyt v populaci, a tudíž nelze k hodnocení použít odhad relativního rizika. Standardem pro tento typ retrospektivní studie je odhad poměru šancí OR.
Bez ohledu na jejich nevýhody zažívají retrospektivní observační studie v současnosti renezanci, která souvisí s nastupující érou personalizované medicíny a s rozvojem biomarkerů. Je‑li totiž množství markerů (expozičních parametrů), jež je nutno kontrolovat, příliš velké, nemohou je randomizační plány observačních studií obsáhnout. Z tohoto důvodu je kvalitě observačních studií věnována velká pozornost i v recentní vědecké a metodické literatuře. Čtenářům doporučujeme např. metodický portál prezentující tzv. „STROBE Criteria“, tedy kritéria pro realizaci kvalitních observačních populačních studií (STROBE: STrengthening the Reporting of OBservational studies in Epidemiology; http:/ / www.strobe‑ statement.org). Tato kritéria jsou velmi podstatná, což dokládá i fakt, že je za svá přijala řada významných mezinárodních vědeckých časopisů. Hlavním metodickým aspektům z této oblasti budeme věnovat některý z dalších dílů seriálu.
doc. RNDr. Ladislav Dušek, Dr.
Institut biostatistiky a analýz
MU, Brno
e‑mail: dusek@iba.muni.cz
Štítky
Detská neurológia Neurochirurgia NeurológiaČlánok vyšiel v časopise
Česká a slovenská neurologie a neurochirurgie

2014 Číslo 4
- Metamizol jako analgetikum první volby: kdy, pro koho, jak a proč?
- Kombinace metamizol/paracetamol v léčbě pooperační bolesti u zákroků v rámci jednodenní chirurgie
- Fixní kombinace paracetamol/kodein nabízí synergické analgetické účinky
- Tramadol a paracetamol v tlumení poextrakční bolesti
- Kombinace paracetamolu s kodeinem snižuje pooperační bolest i potřebu záchranné medikace
Najčítanejšie v tomto čísle
- Vyšetření senzitivity
- Spinální arteriovenózní malformace – dvě kazuistiky
- Genetická variabilita u poruchy pozornosti s hyperaktivitou (ADHD)
- Přínos opakování nepotvrzujícího testu mnohočetné latence usnutí (MSLT) pro stanovení diagnózy narkolepsie
