POČÍTAČOVÉ ZPRACOVÁNÍ DAT ZÍSKANÝCH POMOCÍ POVRCHOVÉHO EMG

Súhrn

V článku se zabýváme základními pravidly počítačového zpracování dat získaných prostřednictvím povrchové elektromyografie. Poukazujeme na důležitost správného nastavení jednotlivých parametrů rychlé Fourierovy transformace, která patří mezi základní metody spektrální analýzy biologických signálů.

Klíčová slova:
sEMG, povrchová elektromyografie, rychlá Fourierova transformace, FFT, vzorkovací frekvence, spektrální analýza

ÚVOD

Sval, z  elektrofyziologického pohledu, představuje generátor elektrické aktivity, kterou lze registrovat prostřednictvím povrchové či jehlové elektromyografie. Tato elektrická aktivita do určité míry koresponduje s výstupní svalovou sílou, vztah však není lineární a je ovlivněn řadou fyziologických, mechanických a elektrických změn (8). Motorická jednotka (MJ), která je tvořena různým počtem svalových vláken, představuje základní funkční jednotku svalové činnosti. V průběhu kontrakce svalu dochází k časoprostorové aktivaci motorických jednotek, jejichž elektrickou sumační odpověď registrujeme pomocí elektromyografie.

ELEKTROMYOGRAFICKÉ ASPEKTY SVALOVÉ KONTRAKCE

Akční potenciál z jednotlivých svalových vláken je konstantní ve své amplitudě i tvaru. Při extracelulárním snímání však závisí na poloze elektrody vzhledem k aktivnímu svalovému vláknu. Ve zdravém svalu vznikají akční potenciály jen aktivací nervových vláken a přechodem přes nervosvalovou ploténku. Proto všechna vlákna patřící do jedné motorické jednotky jsou aktivována simultánně a tvar odpovědi závisí na množství svalových vláken a na jejich umístnění vzhledem k elektrodě (3). Pro volní aktivaci motorické jednotky je typické, že „pálí“ semirytmicky, tedy přibližně o stejné frekvenci. Při zvyšování volní kontrakce dochází ke dvěma paralelním dějům, jednak k časovému náboru vedoucímu ke zvyšování frekvence pálení z počáteční frekvence kolem 4-5 Hz až k frekvenci zhruba 50 Hz (dochází k tetanickému stahu), a jednak k prostorovému náboru MJ, kdy dochází k aktivaci dalších dosud neaktivovaných MJ s vyšším prahem dráždivosti. Při maximální kontrakci fyziologicky dostáváme tzv. interferenční vzorec, který je charakterizovaný „překrýváním“ elektrické aktivity jednotlivých MJ. Hustota interferenčního vzorce je měřítkem počtu funkčních motorických jednotek (1).

PŘEVOD EMG SIGNÁLU DO ČÍSLICOVÉHO TVARU

Cílem vyhodnocení veškerých biosignálů je extrakce informace, která je v nich ukryta. Je však potřebné dodržet určitá metodická pravidla, v opačném případě je riziko ztráty informace a následné desinterpretace velmi vysoké. Elektromyografie je velmi užitečnou objektivizační metodou, která se však dá velmi snadno zneužít.

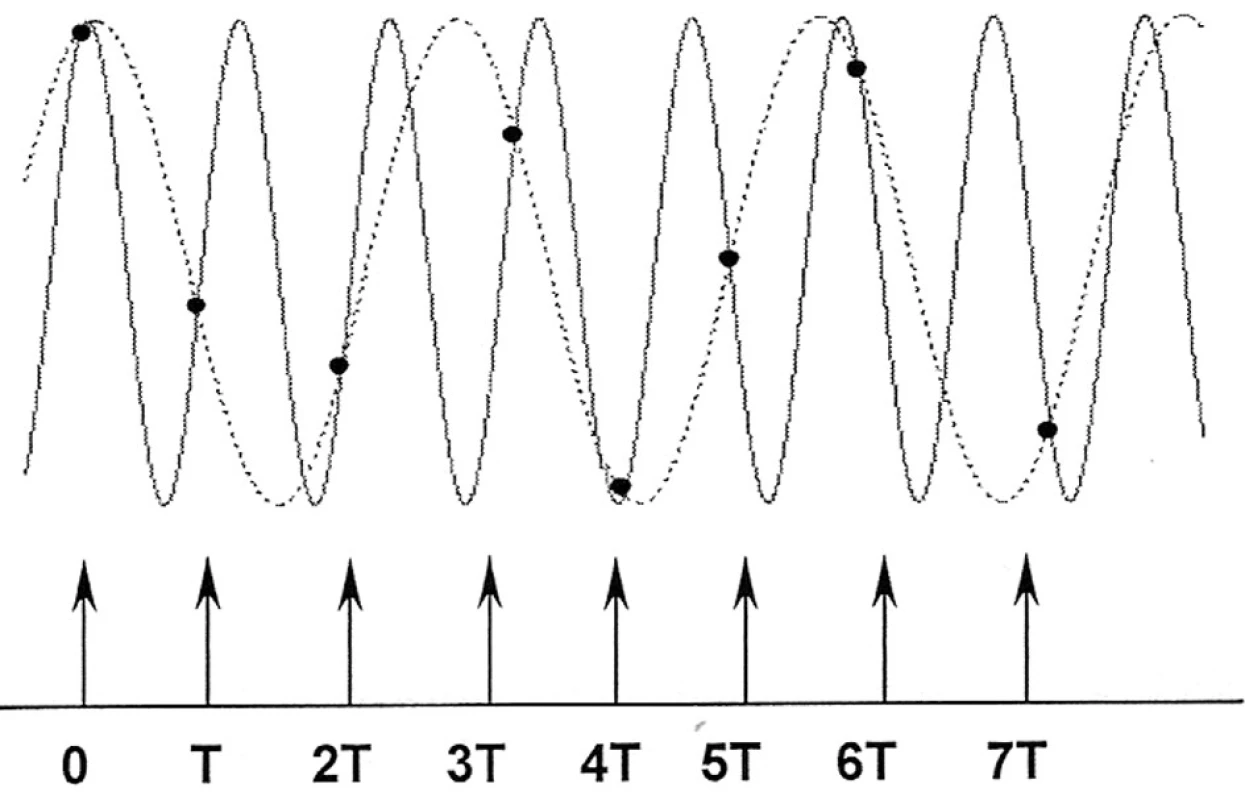
Původní naměřený signál - analogový signál - je spojitý a měřený v μV. Tento signál musíme převést do tzv. diskrétního signálu,neboli digitalizovaného výsledného signálu. Signál je však nutné před převodem filtrovat, a to ze dvou důvodů: 1. k potlačení artefaktů, 2.s ohledem na zvolení minimální nutné vzorkovací frekvence. Vlastní proces digitalizace probíhá prostřednictvím analogově/digitálního převodníku. Původní spojitý elektrický biosignál je převeden na diskrétní posloupnost vzorků signálu, vybraných v pravidelných časových intervalech (4, 7). Velmi důležitým okamžikem je však výběr optimální vzorkovací frekvence F_SAMP. Pokud je příliš nízká, tak dochází k jevu nazývanému „aliasing“, tj k maskování vyšších frekvencí jako nižší frekvence, které je způsobeno podvzorkováním (obr. 1). Pokud je příliš vysoká, tak neúměrně zatěžuje paměť počítače. Řešení problému přinesl Nyquistův teorém, který definuje minimální nutnou vzorkovací frekvenci jako alespoň dvojnásobnou k nejvyšší frekvenci obsažené v naměřeném signálu (Nyquistova frekvence F_NY). Tuto nejvyšší frekvenci signálu určujeme, před převodem analogového signálu do diskrétního, nastavením pásmové propusti prostřednictvím analogových filtrů. V případě povrchového EMG je obvykle pásmová propust 5-500 Hz, nejvyšší obsažená frekvence v signálu je 500 Hz (Nyquistova frekvence) a vzorkovací frekvence musí být minimálně dvojnásobná, tedy:

F_SAMP≥ 2x500Hz ≥ 1000Hz.

Takto získaný diskrétní signál je již připraven k aplikaci celé řády nejrůznějších matematických postupů, z nichž spektrální analýza představuje významnou část analýzy biologických signálů.

SPEKTRÁLNÍ ANALÝZA BIOLOGICKÉHO SIGNÁLU

Spektrální (frekvenční) analýza se snaží zjistit, z jakých frekvenčních komponent je výsledná křivka složena. Předpokládá se, že každý periodický signál lze interpretovat váženým součtem základních (bazických) sinusovek a kosinusovek o příslušné amplitudě a frekvenci. Zaneseme-li tyto základní frekvence a jejich amplitudy (spektrální čáry) do grafu, získáme frekvenční spektrum – závislost amplitudy sinusovek na frekvenci. Měříme je v jednotkách μV²/Hz (výkonová spektrální hustota) nebo μV/√Hz (amplitudové spektrum) (4, 6, 7, 10, 12).

Jednotlivé metody frekvenční analýzy můžeme rozdělit do dvou základní kategorií:

1. Neparametrické metody, které lze použít pro libovolné signály, jejichž typickým přestavitelem je rychlá Fourierirova transformace (FFT).
2. Parametrické metody, které vyžadují stanovení řady parametrů vyhovujících danému matematickému modelu pro zpracovávaný signál. Významným zástupcem této skupiny je tzv. autoregresní model (AR). Dominantní metodou v běžné elektromyografické praxi je rychlá Fourierova transformace (7).

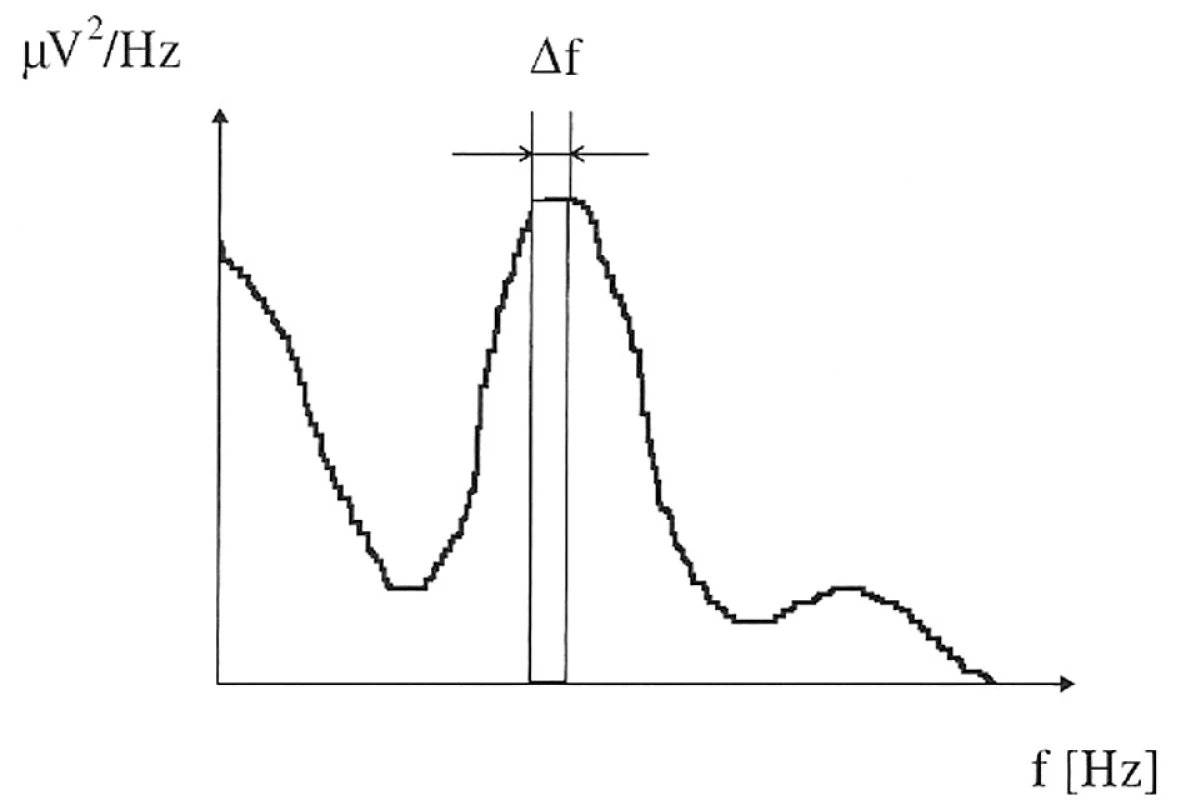
Přestože se frekvenční křivka často vykresluje jako spojitá, je složena podobně jako diskrétní signál z řady jednotlivých spektrálních čár, vzdálených od sebe o diferenci frekvencí ∆f (obr. 2). Rozlišení dvou nejbližších frekvencí ∆f je funkcí intervalu pozorování T.

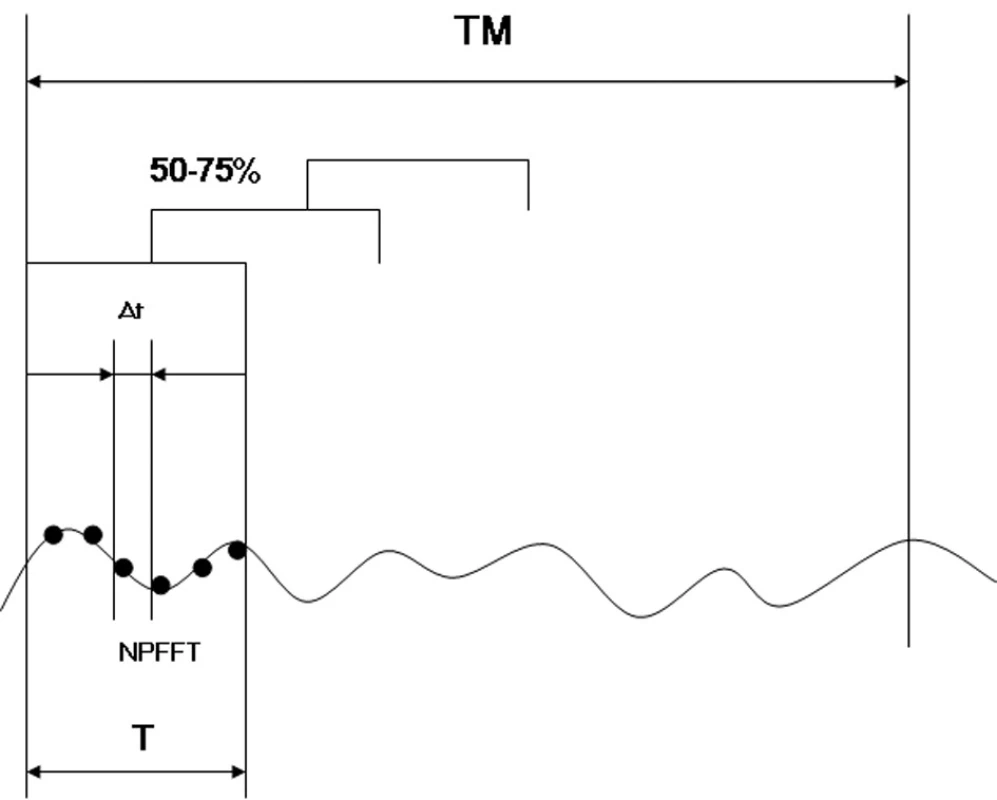
Výsledná spektrální analýza se skládá ze zprůměrnění jednotlivých dílčích epoch (intervalů pozorování T) určených z celkového intervalu vyšetřovaného úseku signálu TM (time of measurement). Interval pozorování T je závislý na parametru počtu bodů Fourierovy transformace, tzv. NPFFT (number of points Fast Fourier transformation). Pro přesnější výpočet spektra pomocí FFT jsou jednotlivé intervaly pozorování T překrývány. Jedna z často používaných metod průměrování periodogramu je Welchova metoda (13), která zajišťuje požadavky na stacionaritu signálu (2, 5, 7, 12).

Vzájemné vztahy mezi ∆t, ∆f, TM, NPFFT a F_SAMP jsou názorně zobrazeny na obrázku 3 a posléze popsány rovnicemi č. 1-3.

TM (time of measurement) – určuje interval sledovaného diskrétního signálu, který bude hodnocen pomocí FFT a je udáván v sekundách. Tento interval je určován manuálně elektromyografistou. Podobně je i určen parametr počtu bodů rychlé Fourierovy transformace, jehož nastavení umožňují všechny EMG programy.

∆t (perioda vzorkování) je definována jako:

T (interval pozorování pro spektrální analýzu) je vyjádřen vztahem

∆f (rozlišení dvou nejbližších frekvencí ve spektru) můžeme popsat rovnicemi

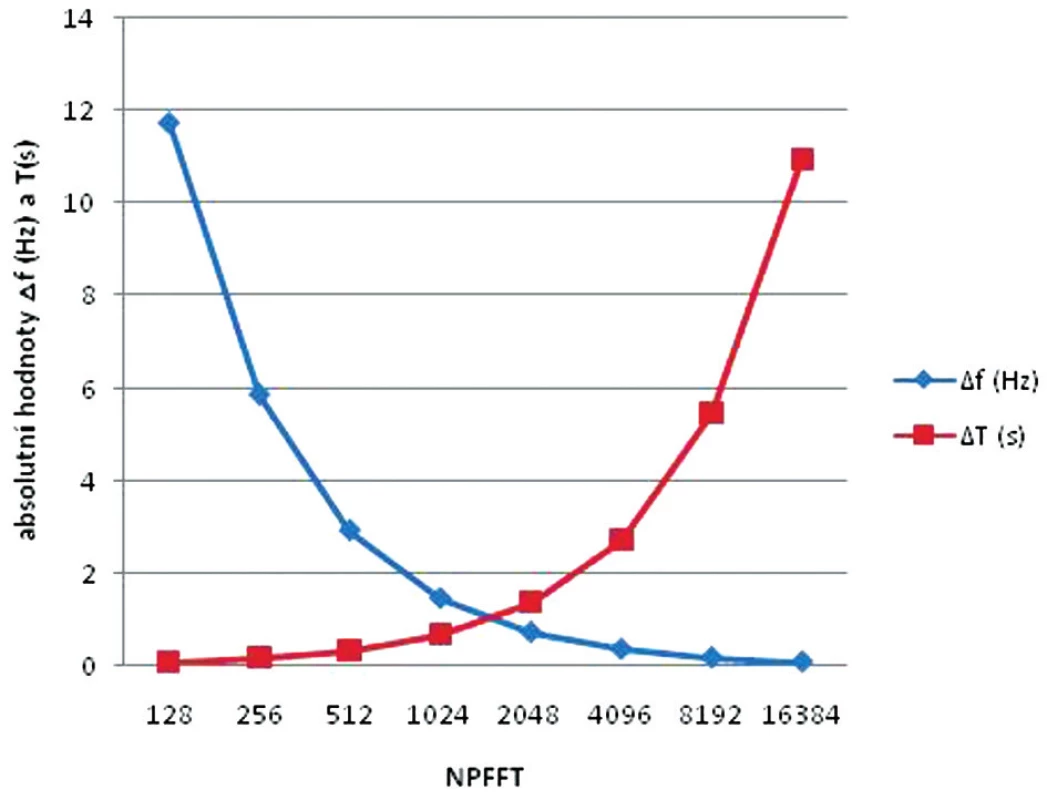
Hodnotíme-li frekvenční charakteristiku signálu, je nutné velmi obezřetně stanovit výše popsané parametry. ∆f nám určuje „jemnost“ frekvenčního rozlišení ve spektrální analýze. Interval pozorování T, v závislosti na celkovém měřeném úseku signálu TM, nám vypovídá o přesnosti výpočtu (počtu zprůměrněných epoch) FFT. Můžeme předpokládat, že čím mají oba parametry ∆f a T nižší hodnotu, tím by mělo být vyhodnocení FFT přesnější. Pokud vezmeme v úvahu stálou vzorkovací frekvenci F_SAMP, např. 1500 Hz (běžně používaná v rutinním povrchovém EMG), pak můžeme nalézt exponenciální nepřímou úměru závislou na počtu bodů FFT mezi intervalem pozorování T a nejbližší vzdáleností dvou spektrálních čár FFT, tzv. ∆f. V tabulce 1 jsme pro ilustraci provedli výpočet jednotlivých parametrů při F_SAMP = 1500 Hz a výsledek graficky zobrazili (obr. 4). Můžeme předpokládat, že čím mají oba parametry ∆f a T nižší hodnotu, tím by mělo být vyhodnocení FFT přesnější.

STACIONARITA SIGNÁLU

Velikost intervalu vyšetřovaného úseku signálu TM (time of measurement) je určující pro množství zprůměrněných epoch (intervalů pozorování T) rychlé Fourierovy transformace (obr. 3). Čím větší je jejich počet, tím přesnější bude výpočet spektrální analýzy pomocí FFT.

V tomto okamžiku však narážíme na problém tzv. stacionarity signálu, kdy se jeho frekvenční a fázové charakteristiky nesmí měnit s časem. Obecně je však známo, že většina biologických signálů nemá stacionární charakter. Příkladem může být studie McEwena (5), který zjistil, že ze všech EEG dat měřených v klidovém stavu, méně než 50 % všech segmentů délky 2,5 až 5s splňovalo podmínku stacionarity a normality. Prakticky to tedy znamená volit úseky pro analýzu co nejkratší. Na druhé straně pro správné vyhodnocení frekvenčního spektra za použití FFT je potřebná délka intervalu vyšetřovaného úseku minimálně 5s. Proto se většina autorů v současnosti shoduje na délce intervalu TM v rozmezí 5-10s, který vyhovuje jak požadavkům stacionarity signálu, tak potřebám pro správné vyhodnocení signálu za použití většiny matematických metod zpracování signálu (4).

ZÁVĚR

V konečných úvahách nad stanovením vhodných parametrů FFT je však nutno nalézt optimální poměr mezi velikostí intervalu pozorování T, rozlišením dvou nejbližších frekvencí ve spektrální analýze ∆f a v neposlední řadě intervalem sledovaného úseku signálu TM v závislosti na stacionaritě signálu. Základní doporučení pro běžnou elektromyografickou praxi jsou následující: vzorkovací frekvence minimálně 1000 Hz, spektrální analýzu hodnotit v časovém intervalu 5-10s a volit počet bodů rychlé Fourierovy transformace 512, 1024 či 2048 bodů. Spektrální analýza je důležitým výchozím krokem k aplikaci dalších matematických postupů, které se především zabývají hledáním shodných složek mezi jednotlivými signály či hodnocením časových zpoždění, která jsou klíčová pro sledování např. rychlosti vedení akčního potenciálu na svalovém vláknu (9).

Příspěvek vznikl s podporou VZ MŠMT ČR MSM 0021620864.

MUDr. David Pánek, Ph.D.

Katedra fyzioterapie FTVS UK

J. Martího 31

162 52 Praha 6

e-mail: panek@ftvs.cuni.cz