Detekce pulsačních změn průměru tepen v dynamickém ultrazvukovém obraze

Súhrn

Pulsační změny průměru cév nesou důležitou informaci o mechanických a elastických vlastnostech cévní stěny a mohou být velmi užitečným nástrojem při hodnocení funkčního stavu a diagnostice mnoha onemocnění vaskulárního systému.

Změny průměru cév jsme posuzovali v dynamickém ultrazvukovém obraze stehenní tepny v podélném řezu. Zpracování a analýza byly provedeny v programovém prostředí Matlab^®. Ze vstupní videosekvence jsme vytvořili sekvenci jednotlivých obrazů, které jsme pro lepší výsledky detekce upravili některými základními metodami předzpracování obrazu a prostředky matematické morfologie s cílem maximálně eliminovat šum a rušivé struktury v obraze. Časově závislý signál změny průměru tepny jsme získali vyhodnocením jasových profilů vedených kolmo na cévní stěnu v celé sekvenci obrazů.

Námi navržený algoritmus detekce pulsačních změn průměru tepen v dynamickém ultrazvukovém obraze se ukázal jako velmi kvalitní nástroj pro hodnocení elastických vlastností tepen. Nevýhodou algoritmu je ovšem jeho silná závislost na vhodných akvizičních parametrech, kvalitě a kompresi vstupních obrazových dat.

Klíčová slova:
ultrazvuk, tepny, elasticita, pulsační změny

Úvod

Pulsační změny průměru cév nesou důležitou informaci o mechanických a elastických vlastnostech cévní stěny a mohou být velmi užitečným nástrojem při hodnocení funkčního stavu a diagnostice mnoha onemocnění vaskulárního systému.

Pulsace cév vznikají rytmickou činností srdce a jsou projevem tlakových změn v cévním systému. Vypuzením krve z levé srdeční komory do cévního řečiště je generována dopředná pulsová vlna, která se šíří stěnami tepen do periferie. Na tepenných větveních a místech s odlišnými vlastnostmi cévní stěny dochází k odrazu pulsové vlny a jejímu šíření zpět k srdci. Výsledný tvar pulsové vlny v daném místě cévního systému je dán prostorovým a časovým součtem dopředné a zpětně odražené vlny. Rychlost šíření a tvar pulsové vlny závisí na stavbě cévní stěny (např. poměr mezi poloměrem cévy a tloušťkou cévní stěny, podíl vláken elastinu, kolagenu a svalových vláken), mechanických vlastnostech cév, krevním tlaku, periferním odporu a dynamických vlastnostech krve (např. viskozita). Velikost pulsové vlny osciluje kolem středního tlaku mezi diastolickým a systolickým tlakem krve.

Šíření pulsové vlny se projevuje změnami tlaku (tlaková vlna), změnami objemu (objemová vlna) a změnami toku krve (proudová vlna). Tlakové změny ve vaskulárním systému vznikají rytmickým stahováním (systola) a uvolňováním (diastola) srdečního svalu. Změny toku krve a změny objemu jsou důsledkem tlakových změn. Objemové změny se projevují roztažitelností cév, změny toku krve lze pozorovat jako urychlení nebo zpomalení toku.

Tlakové vlny v cévním systému lze měřit invazivně zavedením katétru s tlakovým snímačem přímo do cévy, nebo neinvazivně – sfygmograficky. Pro detekci změn objemu cév se používají pletysmografické metody, oscilometrické metody nebo metody aplanační tonometrie. Měření proudových vln lze provést pomocí dopplerovských průtokoměrů nebo průtokoměrů založených na elektromagnetické indukci.

Mechanické vlastnosti látek závisí především na mezimolekulových vazbách a na mikroskopickém i makroskopickém uspořádání molekul. Mezi důležité mechanické vlastnosti látek patří pružnost (elasticita), která se definuje jako schopnost látky vrátit se po odeznění deformující síly zpět do původního tvaru. Mechanické vlastnosti cév, se od matematických modelů odlišují nelinearitou, anizotropií, poddajností cévní stěny a schopností pasivně i aktivně měnit svůj průsvit. Tyto vlastnosti jsou podmíněny přítomností tří strukturních prvků v cévní stěně: vláken elastinu, kolagenu a hladkého svalstva.

Elastické vlastnosti látek lze nejlépe popsat Hookovým zákonem, který vyjadřuje lineární vztah mezi deformací tělesa (ɛ) a vnějším napětím (σ), tj. silou, která tuto deformaci způsobuje. Konstantou úměrnosti je materiálová konstanta – Youngův modul pružnosti (E):

Deformaci tělesa popisujeme jako relativní změnu rozměrů vzhledem k původním rozměrům tělesa. Deformaci (ɛ) cévy tedy můžeme snadno vyjádřit např. jako relativní změnu poloměru cévy (Δr) vzhledem k počátečnímu poloměru (r₀):

Napětí (σ) působící na cévní stěnu je podle Laplaceova zákona přímo úměrné tlaku krve (p) uvnitř cévy a poloměru cévy (r₀) a nepřímo úměrné tloušťce cévní stěny (h):

Vztah pro výpočet elasticity cévní stěny potom můžeme získat dosazením rovnice (2) a (3) do Hookova zákona (1):

Metodika

Změny průměru cév v důsledku tlakových pulsací jsme posuzovali v dynamickém ultrazvukovém obraze stehenní tepny (a. femoralis) v podélném řezu, nasnímaném na ultrazvukovém přístroji GE Logiq C5 lineární sondou s frekvencí 11 MHz. Zpracování a analýzu dat jsme provedli v programovém prostředí Matlab^® R2011b. Ze vstupní videosekvence zájmové oblasti ve formátu *.avi (W = 532 x H = 432 px, 32 fps) o délce 8 sekund jsme vytvořili sekvenci jednotlivých obrazů ve formátu *.png.

Barevné obrazy jsme pro zjednodušení analýzy nejprve převedli do šedotónové stupnice. Výsledek transformace jsme získali jednoduše jako váhovaný součet hodnot v jednotlivých barevných kanálech Red-Green-Blue/Červená-Zelená-Modrá (5). Pro převod jsme zvolili běžně používané váhovací koeficienty: a = 0.2989, b = 0.5870 a c = 0.1140.

Pro lepší výsledky detekce jsme obrazy dále upravili některými základními metodami předzpracování obra-zu (doostření, vyhlazení, úprava jasu, úprava spektra) a prostředky matematické morfologie (eroze, dilatace, uzavření, otevření) s cílem maximálně eliminovat šum a rušivé struktury v obraze.

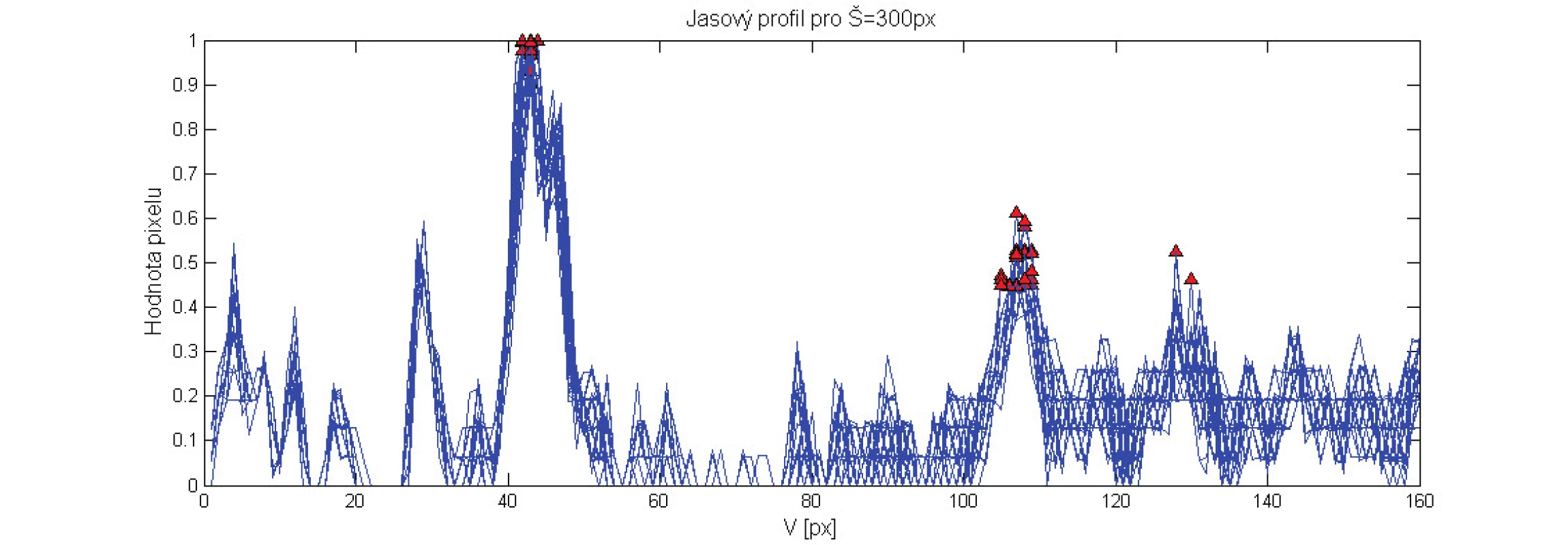
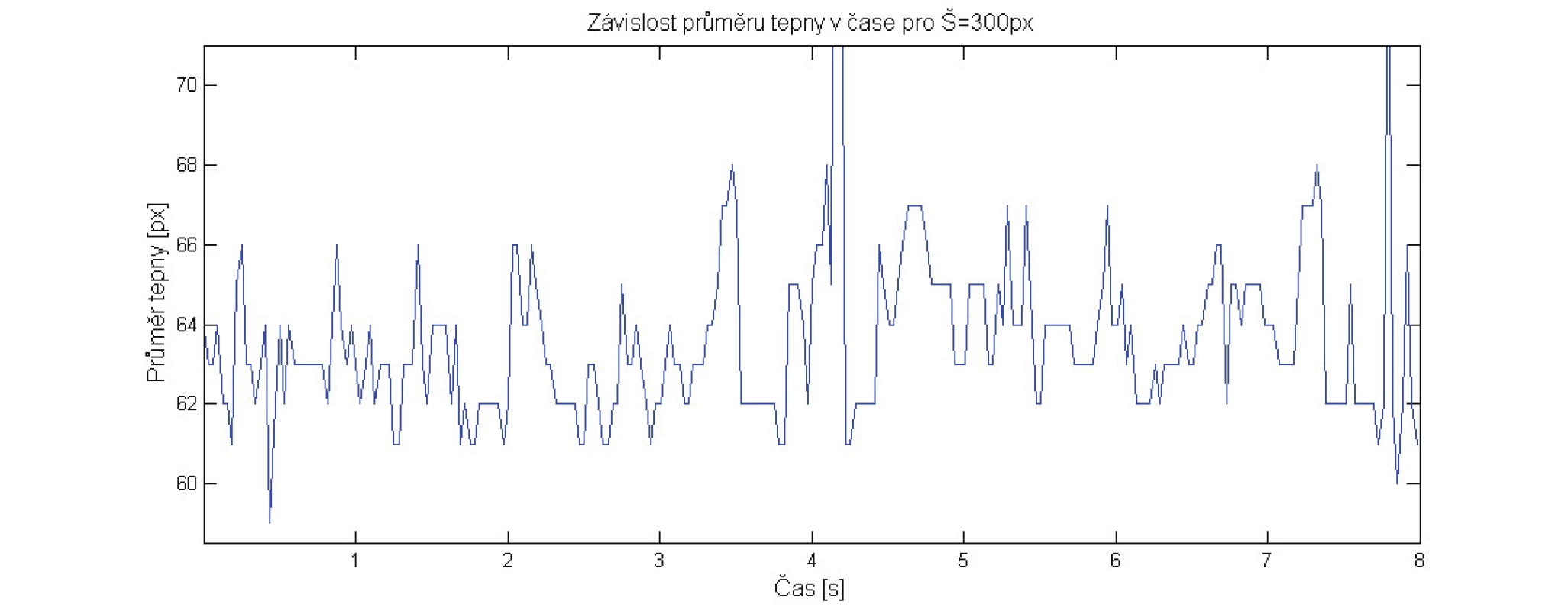
Časově závislý signál změny průměru tepny jsme získali vyhodnocením jasových profilů vedených kol-mo na cévní stěnu v celé sekvenci obrazů. Ukázka upraveného vstupního snímku s vyznačeným směrem pro získání jasového profilu (sloupec W=300 px obrazu) je na Obr. 1. V získaných profilech jasu ze všech obrazů sekvence (viz Obr. 2) jsme s vhodně nastavenými parametry vyhledali pozice maxim dvojic jasových píků, které odpovídaly oběma hranám cévní stěny. Z rozdílů pozic těchto dvojic píků jsme získali informaci o vzájemné vzdálenosti obou stěn cévy a také o změnách průměru tepny v čase (viz Obr. 3).

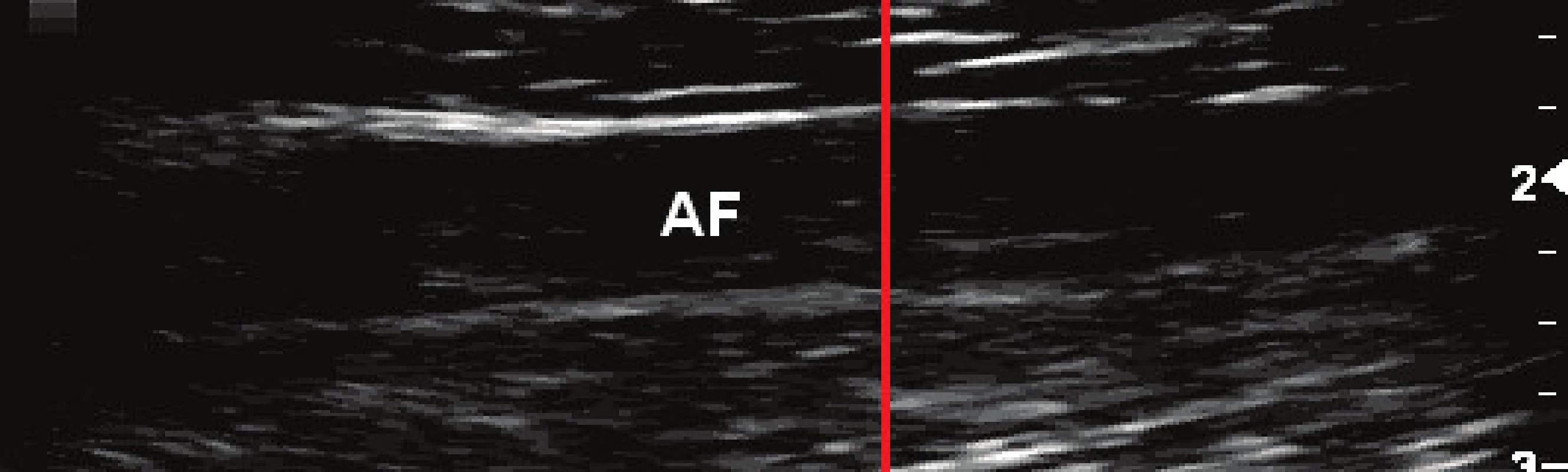
Elastické vlastnosti stehenní tepny jsme stanovili podle rovnice (4) ze znalosti tlaku krve, časových změn průměru tepny a tloušťky cévní stěny. Tloušťku stěny tepny jsme odhadli jako šířku jasového píku v polovině jeho výšky (Full Width at Half Maximum – FWHM).

Výsledky

Lumen tepny je v ultrazvukovém obraze silně hypoechogenní ve srovnání s okolní tkání, proto jsou na jasových profilech poměrně dobře patrné píky odpovídající oběma stěnám tepny (viz Obr. 2).

Závislost průměru stehenní tepny v čase je na Obr. 3. V signálu lze rozpoznat jednotlivé změny způsobené srdeční činností. Průměr tepny se během každého srdečního cyklu měnil od hodnot cca d = 61 pixelů (= 6,29 mm) v diastole (diastolický tlak krve 85 mmHg) až po cca d = 67 pixelů (= 6,91 mm) v systole (systolický tlak krve 135 mmHg). Střední změna průměru tepny mezi diastolou a systolou tedy činila asi Δd = 6 pixelů (= 0,62 mm) při změně tlaku krve p = 50 mmHg. Výrazné odchylky patrné v signálu byly způsobeny chybnou detekcí jasových píků, a pro další výpočty proto nebyly uvažovány.

Protože je poloměr tepny polovinou jejího průměru (r = d/2), spočítali jsme maximální relativní změnu poloměru tepny (deformaci) cca ɛ = 9,85 % vzhledem k rozměrům tepny v diastole (2). Tloušťka tepenné stěny (FWHM) kolísala v širokém rozsahu od cca h = 5 pixelů (= 0,52 mm) až po asi 10 pixelů (= 1,03 mm). Elasticita (4) stehenní tepny potom orientačně vyšla v rozsahu cca 206 až 409 kPa, což přibližně odpovídá fyziologickým hodnotám uváděným v literatuře.

Závěr

Dynamické změny průměru tepen mohou být cenným zdrojem informací o mechanických a elastických vlastnostech cévní stěny. Je známo, že elasticita cév je významný parametr pro posouzení kardiovaskulární morbidity a mortality. Nespornými výhodami hodnocení elastických vlastností cév v ultrazvukových obrazech jsou jednoduchost, nízká cena a bezpečnost metody a také široká dostupnost ultrazvukového vyšetření.

Námi navržený algoritmus detekce pulsačních změn průměru tepen v dynamickém ultrazvukovém obraze se ukázal jako jednoduchý a kvalitní nástroj pro hodnocení a přibližný kvantitativní odhad elastických vlastností tepen. Nevýhodou algoritmu je ovšem jeho silná závislost na vhodných akvizičních parametrech, kvalitě a kompresi vstupních obrazových dat. Kvantitativní stanovení elasticity tepny je tedy pouze přibližným odhadem skutečného stavu.

Ing. Mgr. Martin Sedlář

Biofyzikální ústav

Lékařská fakulta

Masarykova univerzita v Brně

Kamenice 126/3, 625 00 Brno

E-mail: sedlar.m@mail.muni.cz

Tel.: +420 549 492 890