Vliv délky implantátu na jeho primární stabilitu

Súhrn

Dentální implantologie je jednou z nejrychleji se rozvíjejících oblastí stomatologie a implantolog potřebuje mít k dispozici kvalitní vědecky ověřené medicínské informace, aby mohl poskytnou pacientovi to nejlepší, co dnešní věda a trh nabízí.

Dlouhodobé správné fungování zubních implantátů ovlivňuje řada faktorů, mezi které patří design implantátu (čili tvar, povrch, průměr a délka) a chirurgický postup implantace. Předmětem naší práce je posouzení vlivu délky implantátu na jeho primární stabilitu měřenou rezonanční frekvenční analýzou (RFA) a následně zpracovanou sérií parametrických výpočtů s využitím metody konečných prvků.

Klíčová slova:
design implantátu - rezonanční frekvenční analýza (RFA) - metoda konečných prvků - délka implantátu

ÚVOD

Dentální implantáty se staly od začátku 80. let minulého století běžnou součástí stomatologické praxe. Díky poměrně snadnému přístupu při zavádění umožňují, na rozdíl od většiny ostatních implantátů, i relativně snadnou post-operativní kontrolu jejich stavu. Kvalita zavedení, tedy jeho primární stabilita a následná kvalita ukotvení implantátu v kosti (oseointegrace), tj. sekundární stabilita, tvoří dohromady fundamentální informaci pro implantologa.

S vývojem implantátů souvisí i vývoj metodik zjišťování jejich stability. Metodika měření stability implantátu by měla být především: rychlá, snadno opakovatelná, nedestruktivní a zdraví nezávadná. Je potřeba znát její limity a vyvarovat se možným špatným interpretacím.

V minulosti se v klinické praxi používalo mnoho metod: můžeme zmínit RTG snímky, měření potřebného vytočovacího momentu a histologické rozbory. Další metodou bylo stanovení stability pomocí vibrační analýzy, a to buď přechodnou nebo kontinuální excitací. Na principu přechodné excitace je založen Periotest (Siemens, Bensheim, Německo) [10], původně vyvinutý ke stanovení charakteristik vlastního zubu. Postupně se však pro svou jednoduchost začal hojně využívat i k určování stability implantátů.

Nejnovější a patrně i nejpřesnější metoda je založena na kontinuální excitaci, čili na rezonanční frekvenční analýze (RFA) [16]. První prototyp, který využívá RFA pro zjišťování stability dentálních implantátů, byl sestrojen profesorem Neilem Meredithem začátkem devadesátých let [7, 8, 9, 10]. Následně byl přístroj rozšířen pod obchodní značkou Osstell (Integration Diagnostic AB, Sweden) [12]. V současné době přístroj dospěl do třetí generace a prodává se pod obchodní značkou Osstell Mentor [11, 15]. Osstell^® měří rezonanční frekvenci pomocí snímače obsahujícího dvojici piezoelementů, umístěných v segmentu ve tvaru L, který je fixačním šroubem připevněn k implantátu. První piezoelement slouží k rozkmitání celé soustavy (tj. L-segmentu, implantátu a periimplantátové kosti) periodickým sinusovým signálem o frekvenci stoupající od 5 do 15 kHz [10, 13]. Druhý piezoelement registruje odezvu, tedy rezonanční frekvenci. Vyšší naměřené rezonanční frekvence by měly odpovídat vyšší stabilitě implantátu [4, 5, 6]. Zjištěná rezonanční frekvence je automaticky přepočítávána na Implant Stability Quotient (ISQ), který je v rozsahu od 0 do 100 [12]. Závislost ISQ na rezonanční frekvenci je lineární [15]. Hodnota ISQ je zobrazena na displeji. Současně se na displeji vykreslí i graf amplitudového spektra, ze kterého lze usoudit na validitu měření [14, 12].

Při interpretaci výsledků je potřeba znát limity přístroje, které ovlivňují výsledné hodnoty stability. Je zcela evidentní, že přístroj neměří pouze kvalitu spojení implantát–kost, ale výsledná hodnota je ovlivněna řadou biomechanických parametrů. Pro některé parametry je snímač kalibrován individuálně. Utahovací moment, vyvinutý při dotahování fixačního šroubku a snímače, se ukázal jako prakticky nevýznamný [2, 17]. Vliv finálního kroutícího momentu při zavádění implantátu do kosti na výsledné ISQ ale dle námi dostupných informací nebyl dosud zkoumán.

Další parametry, které ovlivňují výslednou hodnotu primární stability, jsou materiálové vlastnosti kostní tkáně a tvar implantátu. Další souvisejí se samotným přístrojem. V literatuře [14, 15] bylo ukázáno, že přístroj v některých případech nezaznamenává první vlastní frekvenci, ale zachycuje až frekvence vyšší, a to v případě, že první frekvence neleží v měřitelném pásmu [1]. Jiné studie ukazují, že výsledek primární stability je výrazně ovlivněn orientací snímače [13, 17].

Tato studie je zaměřená na prokázání vlivu délky implantátu na výsledné hodnoty primární stability.

MATERIÁL A METODIKA

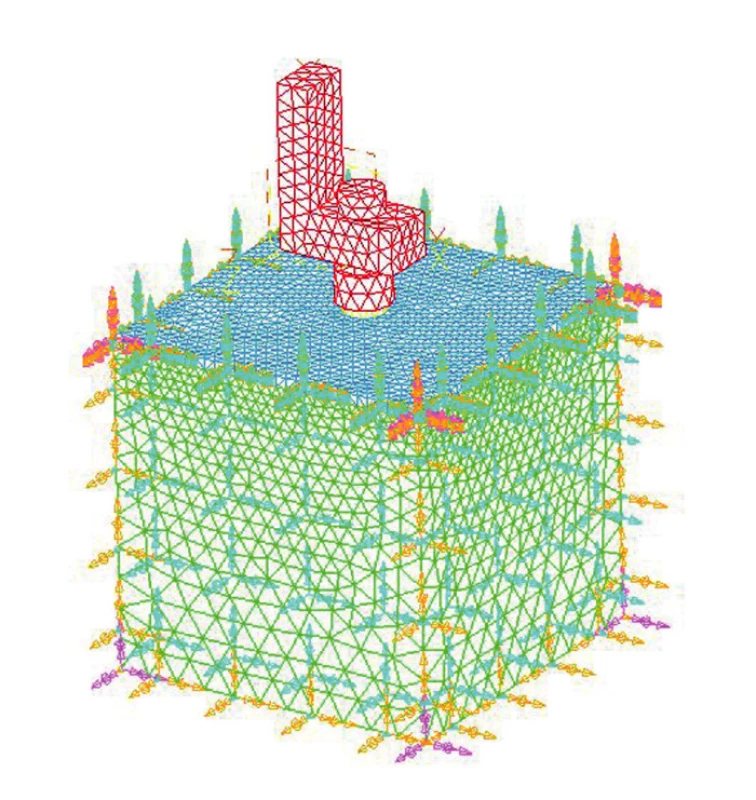
Zadání bylo řešeno pomocí série parametrických výpočtů s využitím metody konečných prvků [3] v programu I-deas 9 (Siemens PLM Software, Texas). Konečno-prvkový model L segmentu, implantátu a kostní tkáně byl namodelován následovně: L segment odpovídá použitému při experimentech, implantát byl zjednodušen tím, že nebereme v úvahu závit a kostní tkáň modelujeme jako homogenní-izotropní materiál. Implantaci považujeme za unikortikální, síla kortikální kosti je 1 mm. Jako prvek byl použit čtyřuzlový čtyřstěn.

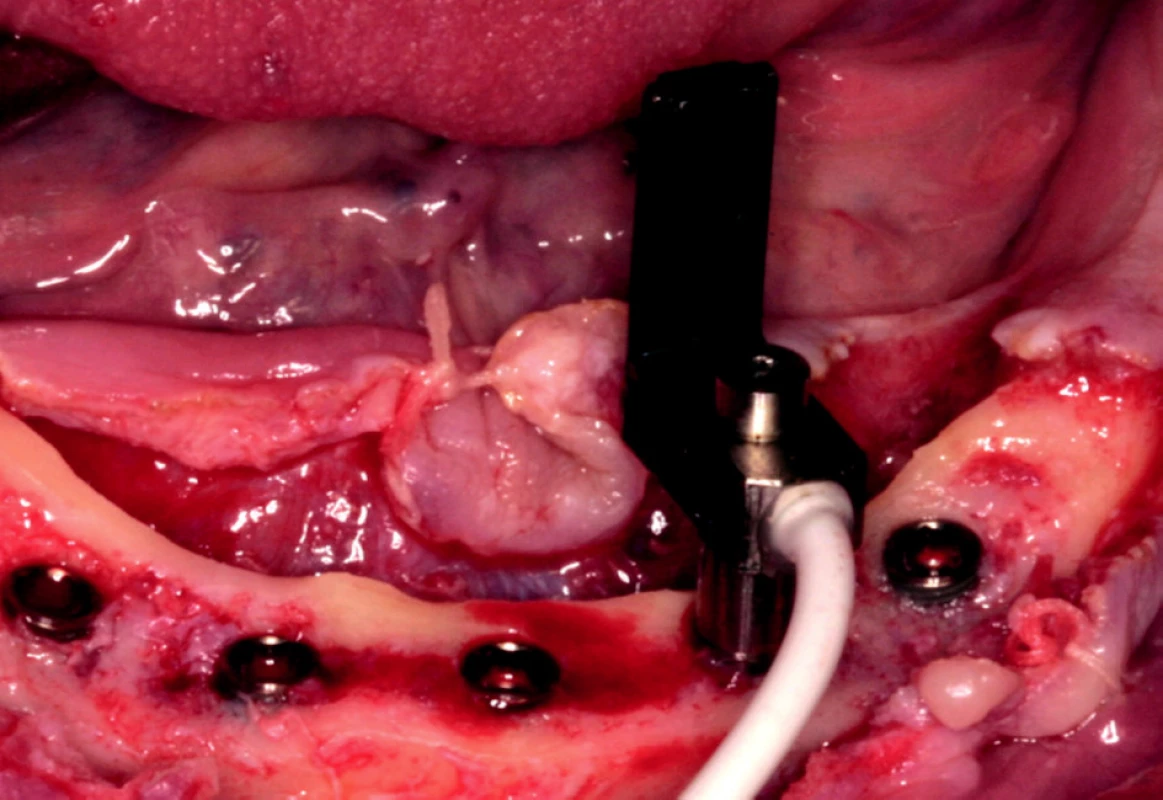
Geometrie bloku kostní tkáně byla tvořena kvádrem 30x30x30 mm (obr. 1), délka implantátu byla volena 10, 12, 14 a 16 mm a průměr všech implantátů byl 3,7 mm. Do experimentu bylo zahrnuto celkem 32 pacientů (18 žen a 14 mužů), u nichž byly zavedeny do dolní čelisti v rozsahu 46–36 implantáty firmy Lasak Impladent STI-BIO-C. Snímač byl vždy orientován kolmo na dlouhou osu alveolu (obr. 2), přičemž rameno L segmentu je umístěno orálně. Výsledné hodnoty primární stability ISQ byly zaznamenány a zpracovány v matematickém programu.

VÝSLEDKY

Z naměřených hodnot jsme stanovili pro příslušné délky průměrné hodnoty. Ze závislosti (je lineární) můžeme vidět, že hodnoty primární stability se zvyšují s délkou implantátu (graf 1, graf 2). Maximální hodnoty průměrných ISQ jsou nejvyšší pro implantát délky 16 mm s hodnotou 69,63 a nejnižší pro implantát délky 10 mm s hodnotou 63,25. Typ závislosti se shoduje jak pro experiment, tak i pro numerické výpočty.

DISKUSE

Naměřené a vypočtené závislosti můžeme vysvětlit z pohledu základů kmitání. Z nich vyplývá, že rezonanční frekvence (pro zjednodušený model) jsou závislé na tuhosti a hmotnosti dle následujícího vzorce:

kde Ω je rezonanční frekvence, k tuhost soustavy a m její hmotnost.

Obecně ale nelze dopředu říci, zdali pro zvyšující se délku implantátu poroste rezonanční frekvence. Ze vzorce je patrné, že rezonanční frekvence závisí na dvou parametrech m a k, přičemž délka implantátu je obsažena v obou, čili délka mění nejen hmotnost, ale i tuhost soustavy.

Vliv jednotlivých parametrů (hmotnosti a tuhosti soustavy) na rezonanční frekvenci můžeme vidět na grafech. Graf 3 popisuje obecně platnou závislost vlastní frekvence na tuhosti soustavy při konstantní hmotnosti soustavy a graf 4 popisuje obecně platnou závislost vlastní frekvence na hmotnosti soustavy při konstantní tuhosti soustavy.

Z naměřené a vypočítané závislosti vidíme, že se zvyšující se délkou implantátů (při zachování jejich průměrů) stoupají hodnoty primární stability. Čili hodnoty rezonančních frekvencí jsou přímo závislé na délce implantátu. Z tohoto lze usuzovat, že délka implantátu se větší měrou podílí na zvýšení tuhosti systému než na zvýšení jeho hmotnosti, a proto s délkou implantátu (při stejném průměru) stoupá jeho primární stabilita.

Při znalosti popsaných zákonitostí pak vyšší primární stabilita u tappered implantátů ve srovnání s klasickými šroubovými implantáty je vysvětlitelná i tak, že vzhledem ke svému tvaru má tappered implantát nižší hmotnost. Porovnání těchto dvou typů implantátů a matematické vyjádření závislostí jejich tvarů a primární stability je předmětem našich dalších měření.

ZÁVĚR

Je velmi dobře známo, že primární stabilita závisí na chirurgickém postupu, kvalitě kosti a na designu implantátu. Do něj řadíme tvar, povrch, délku a průměr implantátu. Z těchto charakteristik je ve světové i domácí literatuře nejmenší pozornost věnována právě délce, která primární stabilitu ovlivňuje tak, že s prodlužující se délkou implantátu primární stabilita stoupá.

Znalosti a pochopení zákonitostí designu implantátu jsou nezbytnou součástí každého předimplantačního procesu, při kterém plánujeme budoucí zákrok. Bez implementace těchto zákonitostí do praxe se žádný implantolog dnes ani v budoucnu neobejde.

Věnováno prof. MUDr. Jiřímu Vaňkovi, CSc., k jeho významnému životnímu jubileu.

Prim. MUDr. Ladislav Dzan

Oddělení ústní, čelistní a obličejové chirurgie

KN Liberec, a.s.

Husova 10

460 63 Liberec 1

e-mail: ladislav.dzan@seznam.cz