Kinematika hlasivek - nové parametry hodnocení

Souhrn

V práci jsou shrnuty nové poznatky o kinematice hlasivek, získané užitím vysokorychlostní kamery HSV. Standardně používané parametry hodnocení hlasivkové kinematiky jsou rozšířeny o nové, získané použitím metod, vycházejících z detekce hlasivkové štěrbiny a stanovení její hlavní osy. Na vybraných kazuistikách jsou dokumentovány parametry symetrie štěrbiny a pohybu těžiště hlasivkové štěrbiny vzhledem k její ose.

Klíčová slova:
laryngologie, hlasové ústrojí, glottis, kvalita hlasu, laryngoskopie, měření tvorby hlasu

1. ÚVOD

Vyšetření kinematiky hlasivek pomocí vysokorychlostní kamery (HSV) provádíme na naší klinice již 10 let. Záznam vyšetření nám umožňuje sledovat ve zpomalené, časově rozložené formě, reálný pohyb hlasivek. K ohodnocení kinematiky hlasivek nemusí být vždy ale samotné pozorování dostatečné. Zdá se, že by bylo účelné definovat takové parametry, které charakterizují změny tvaru hlasivkové štěrbiny v čase v průběhu jedné nebo více period. Na základě těchto parametrů by mohla být stanovena kritéria pro hodnocení kvality kinematiky hlasivek.

Pro analýzu videozáznamů HSV je v současnosti k dispozici nejrozšířenější firemní software společností Richard Wolf GmbH [23] a KayPENTAX [24]. Tyto software umožňují většinou vytvoření videokymogramu v libovolném místě hlasivkové štěrbiny, ruční nebo poloautomatickou detekci hlasivkové štěrbiny, ruční definování hlavní osy hlasivek a výpočet a zobrazení průběhu časových změn v kinematice pevně zadaných bodů hranice a velikosti plochy hlasivkové štěrbiny. Dále umožňují vizualizaci a seřazení jednotlivých snímků z videosekvence na jednu obrazovku tak, že lze pozorováním určit okamžik otevření a uzavření hlasivkové štěrbiny, resp. dobu otevírání a uzavírání hlasivek. Lze vypočítat tzv. Open Quotient (OQ), popř. zachytit změnu jasu v předem definovaných bodech na hlasivce v průběhu jedné nebo více period. Při hodnocení některých výsledků, které splňují nutné předpoklady, se používá pro získání další třídy parametrů Fourierova analýza (FFT).

Dlouholeté zkušenosti s analýzou parametrů hlasového pole (VRP), multidimenzionální analýzou (MDVA) a analýzou kvality závěru glottis (SCORE) (viz např. 13, 14, 17), nás vedly k myšlence rozšířit soubor parametrů, které jsou součástí komerčních software HSV s cílem dále hledat vhodná kritéria hodnocení kvality kinematiky hlasivek. Abychom mohli takové parametry definovat, testovat a dávat do vzájemných souvislostí a korelací s výsledky vyšetření VRP, MDVA a SCORE, bylo nutné nejprve s dostatečnou mírou spolehlivosti automaticky detekovat hlasivkovou štěrbinu v jednotlivých snímcích videosekvence a stanovit odhad parametrů osy symetrie hlasivkové štěrbiny.

Tato práce proto obsahuje popisy detekce hlasivkové štěrbiny a odhadu osy symetrie hlasivkové štěrbiny a definuje paramet­ry hlasivkové štěrbiny, které jsou od osy symetrie odvozené. Zejména se jedná o nové parametry polohy těžiště hlasivkové štěrbiny a popisy jeho trajektorie ve videosekvenci HSV.

2. ZPŮSOBY DETEKCE HLASIVKOVÉ ŠTĚRBINY

V současné době se hlasivková štěrbina detekuje ručně nebo poloautomaticky se vstupem uživatele. Poloautomatické metody jsou většinou obsažené v proprietárním softwaru, většinou však nejsou přesně popisovány. Nejpoužívanější jsou segmentace typu watershed (4) Gabor filtering (15), region merging (16) a automatické prahování (18). Tyto metody samostatně aplikované ale nemají velkou úspěšnost u komplikovaných snímků s nižší kvalitou. Proto jsou celou řadou autorů používány kombinované metody, viz výběr některých přístupů (1, 2, 3, 11, 20).

My v našich aplikacích pro automatickou detekci hlasivkové štěrbiny používáme dvě metody, metodu Max-Min-Thresholding a metodu shlukové analýzy. Tyto metody pouze informativně představíme.

2.1  Metoda Max-Min-Thresholding

Metoda Max-Min-Thresholding je tvořena posloupností na sebe navazujících procesů a je výsledkem testování řady přístupů a jejich modifikací. Jedná se o procesy z oboru bodových transformací, filtrace, automatického prahování (7, 12) a konstrukce souvislých oblastí ve snímku (19). Jednotlivé procesy jsou aplikovány jak na jednotlivé snímky, tak na celou videosekvenci.

2.2  Metoda shlukové analýzy

Po vyčerpání možností metody Max-Min-Thresholding jsme zvolili pro klasifikaci obrazových bodů metodu shlukové analýzy. Shluková analýza reprezentuje postupy seskupování objektů do více či méně homogenních skupin podle jejich vzájemné podobnosti. Nejpoužívanější metodou shlukové analýzy je MacQueenův algoritmus „učení bez učitele“, tzv. metoda K-means (9).

Při její aplikaci jsme vycházeli ze skutečnosti, že je ve snímku hlasivková štěrbina tmavší než její okolí. To se nejvýrazněji projevuje v červené složce barevného modelu RGB. Jednotlivé obrazové body ve snímku proto považujeme za klasifikované objekty xx_i, i = 1 až n, kde n je počet těchto obrazových bodů. Parametry použité pro popis vlastností obrazových bodů vychází z barevného modelu RGB. Obrazové body rozdělujeme do stanoveného počtu k klasifikačních tříd CLASS_j, pro j = 1 až k. K přiřazování bodů do tříd CLASS_j používáme iterační metodu K-means, jejíž jednotlivé iterační cykly opakujeme, dokud nedosáhneme ustáleného stavu, požadované přesnosti nebo stanového počtu cyklů, tzv. STOP podmínka.

Před zahájením iteračních cyklů je pro každou předpokládanou třídu CLASS_j definován její počáteční hodnotový představitel, tzv. centrum Center_j, pro j = 1 až k (obr. 1a). Dále je provedeno počáteční rozdělení obrazových bodů do klasifikačních tříd CLASS_j (obr. 1b) podle kritéria nejmenší vzdálenosti parametrů bodu, vztah (1) vůči prvotně definovaným centrům Center_j (22),

 Prvním krokem cyklu je vždy výpočet nových center Center_j jednotlivých tříd jako těžiště tříd, vztah (2) nad parametry bodů xx_i, které byly do třídy CLASS_j přiřazeny (obr. 1d).

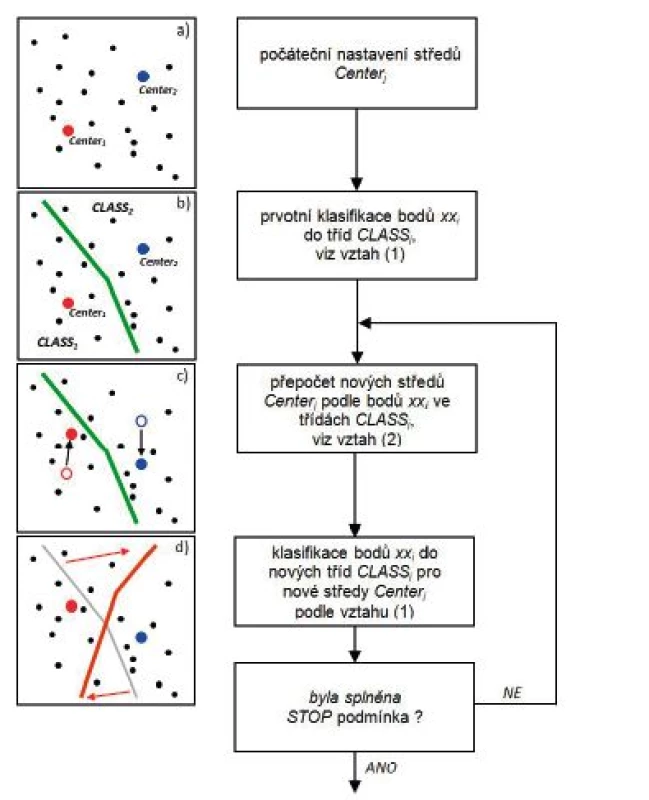
Druhým krokem cyklu je pak opětovné rozdělení obrazových bodů do klasifikačních tříd CLASS_j (obr. 1d) podle kritéria nejmenší vzdálenosti parametrů bodu, vztah (1) vůči nově vypočítaným centrům Center_j,

Tento iterační cyklus se opakuje až do dosažení definované STOP podmínky.

2.3 Testování použitých metod a dosažené výsledky

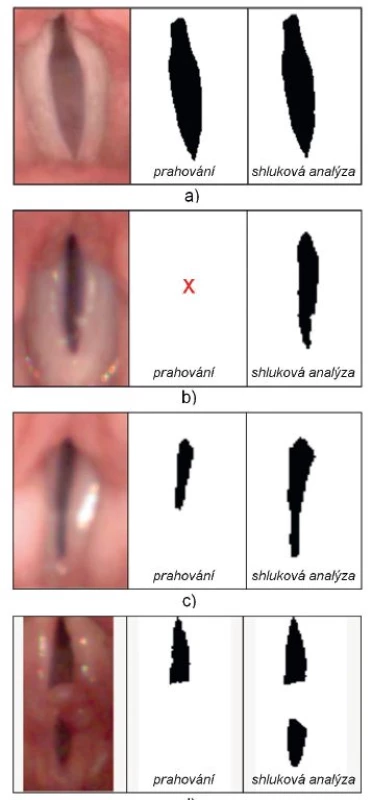
Metoda shlukové analýzy výrazně zvyšuje úspěšnost detekce hlasivkové štěrbiny oproti metodě prahování Max-Min-Thresholding. Při použití vzorku 130 vybraných typových videosekvencí, které byly z hlediska detekce štěrbiny komplikované, byla shlukovou analýzou správně detekována štěrbina v 97 případech, prahováním ve 42 případech. Výsledek metody prahování byl pouze ve 4 případech detekce štěrbiny lepší než u metody shlukové analýzy. Příklady správné detekce a úplného nebo částečného selhání metody Max-Min-Thresholding v porovnání s metodou shlukové analýzy jsou na obrázku 2. Správnost detekce štěrbiny byla vždy posuzována ve spolupráci s otorinolaryngologem.

3. OSA SYMETRIE HLASIVKOVÉ ŠTĚRBINY

Po detekci hlasivkové štěrbiny je nezbytné ve snímcích provést odhad osy symetrie¹ a určit její normálu. Správné stanovení polohy osy symetrie ovlivňuje vypovídací schopnost těch parametrů kinematiky hlasivek, které jsou odvozeny z předpokladu symetrie hlasivek. Takové parametry detekují vzájemné anomálie mezi levou a pravou hlasivkovou řasou. Hlavní osu hlasivky detekujeme automatickou metodou, která pracuje se sekvencí po sobě jdoucích snímků detekované hlasivkové štěrbiny.

3.1  Metoda odhadu osy symetrie

Ve firemním softwaru (23, 24) se většinou automatická detekce osy neprovádí, nebo je poloha osy stanovena ručně dvěma body, které odpovídají poloze přední a zadní komisury. V odborné literatuře jsou však metody automatické detekce hlavní osy hlasivek publikovány (např. 2, 10), nebo přehledová publikace (6).

Metody automatické detekce hlavní osy hlasivek se musí vypořádat s poruchami, které se během snímání videosekvence objeví. Např. vlivem vzájemného pohybu kamery a hrtanu se může poloha, velikost i natočení hlasivek v jednotlivých sekvencích snímků lišit. Dochází k překrytí části hlasivek supraglotickými strukturami, k ořezu štěrbiny na okraji oblasti záznamu, zakrytí jinou anatomickou strukturou nebo zamlžení snímků. Metoda detekce musí proto tyto poruchy v přiměřené míře akceptovat.

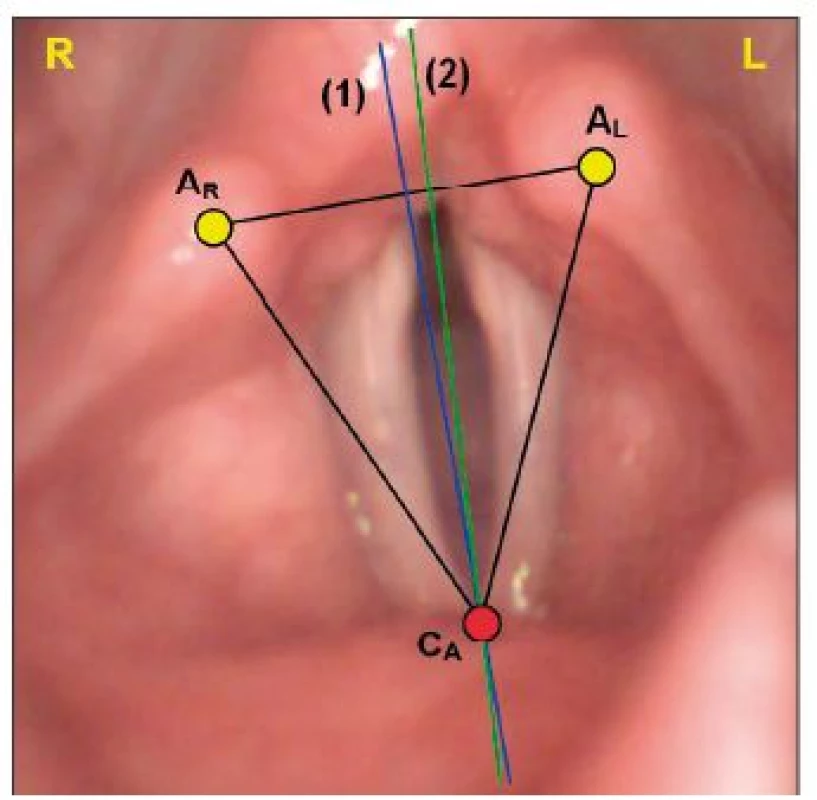
Na základě analýzy chování hlasivek, vývoje polohy hlasivkové štěrbiny vzhledem k umístění přední a zadní komisury a anatomické ose hlasivek (obr. 3) byla vytvořena robustní metoda odhadu parametrů osy symetrie hlasivkové štěrbiny.

Metoda odhadu parametrů osy symetrie hlasivkové štěrbiny vychází z předpokladů:

• a) osa prokládá štěrbinu při uzavřeném stavu,
• b) poloha hlasivek se ve snímcích videosekvence nemění, tj. snímky jsou stejnolehlé,
• c) při nedovírání hlasivek osa prochází středem štěrbiny v nejuzavřenějším stavu.

---

1 Hlavní osa hlasivek [Glottal Main Axis] je definována jako spojnice středů přední a zadní komisury; terminologie a definice byla převzata z Příručky uživatele, HRES ENDOCAM, Richard Wolf (23). Střední linie hlasivkové štěrbiny [Glottal Midline] (10, 11).

2 Anatomická osa hlasivkové štěrbiny vychází z vlastní definice glottis = trojúhelníková štěrbina otevřená při dýchání a uzavřená při fonaci, která je ohraničena laterálně hlasivkovými řasami (plicaes vocalis), a dorzálně interarytenoidním prostorem. Anatomická osa je pak těžnice v trojúhelníku s vrcholem ve středu přední komisury hlasivek a středem vzdálenosti mezi arytenoidními hrboly.

---

Detekce osy ve fázi uzavřené štěrbiny, [předpoklad-a] je velice sporná. Její pozici je ale možné určit podle plochy štěrbiny ve fázi uzavření těsně před a ve fázi otevření těsně po stavu maximálního uzavření. Tato místa jsou evidentně ta, kde se nacházejí body štěrbiny nejčetněji. Hlasivky se ale nemusejí otevírat rovnoměrně po celé jejich délce a jejich pohyb může začínat u jednoho z okrajů. Proto nestačí sledovat chování hlasivek jen těsně před a těsně po stavu jejich maximálního uzavření, ale během celé periody nebo celé videosekvence.

Zde využijeme [předpoklad-b] o stejnolehlosti snímků ve videosekvenci. Promítnutím všech snímků sekvence a sečtením stejnolehlých obrazových bodů získáme matici, která má význam četností výskytů hlasivkové štěrbiny v jednotlivých bodech snímku. Pro vizualizaci takto získané informace vydělíme hodnotu všech bodů počtem snímků v sekvenci. Tím dojde k efektu bodové filtrace průměrováním podle stejnolehlých obrazových bodů a vznikne šedotónový obrázek, ve kterém nejtmavší místa jsou ta, kde je hlasivka nejdéle otevřená. V těchto bodech pak předpokládáme nejvyšší pravděpodobnost umístění osy symetrie hlasivkové štěrbiny (obr. 4a).

Díky technice snímání vysokorychlostní kamerou uvažujeme svislou orientaci osy. Proto v dalším upřesníme její pozici nalezením nejtmavšího (nejčetnějšího) bodu v každém řádku vypočteného snímku. Při nedovírání hlasivkové štěrbiny dochází k výskytu několika stejně tmavých (četných) bodů v jednom řádku. Pak jako bod osy označíme prostřední z nejtmavších bodů [předpoklad-c] (obr. 4b).

Při pořizování záznamu pohybu hlasivek vysokorychlostní kamerou není neobvyklé, že vlivem vzájemného pohybu hrtanu a kamery dochází ke změně polohy hlasivek v sekvenci snímků. V tomto případě je pak porušen [předpoklad-b] o stejnolehlosti jednotlivých snímků během videosekvence. Metoda je proto ještě upravena pro stanovení odhadu pomocí tzv. plovoucí osy.

Vycházíme z toho, že změna polohy hlasivek není díky setrvačné hmotě kamery a vysoké rychlosti snímání v jednotlivých po sobě jdoucích snímcích významná. Při rychlosti snímání 4000 snímků/s a základní hlasivkové frekvenci F_o = 200 Hz, připadá na jednu periodu otevření/uzavření hlasivek 20 snímků, tj. doba jedné periody T_perioda = 5 ms. Pokud však budeme uvažovat délku sekvence více než 100 snímků, bude celková doba T_sekvence ≥ 25 ms a může dojít k posunu o několik obrazových bodů. V takových případech úlohu odhadu osy symetrie hlasivkové štěrbiny ve snímku IM_k videosekvence redukujeme na omezený počet snímků 2m+1, tj. snímky z videosekvence IM_k-m, …, IM_k, … ,IM_k+m. Počet snímků 2m+1 odpovídá jednomu kmitu hlasivek s tím, že sekvence musí vždy obsahovat snímky s maximálním a minimálním otevřením hlasivek.

Aplikací metody tak získáme přímku, která je odhadem osy hlasivkové štěrbiny a zároveň osy předpokládané symetrie (obr. 4).

Takto získané body určují odhad bodů osy hlasivek. Ve většině případů již tvoří přímku nebo ji kopírují v těsné blízkosti. Při poškození hlasivek, např. při rozdělení štěrbiny na více částí, může ale docházet k nepřesnostem. Proto jsme pro upřesnění odhadu osy symetrie hlasivkové štěrbiny, použili metodu lineární regrese (obr. 4c).

3.2  Testování metody odhadu osy hlasivek a dosažené výsledky

Metoda byla aplikována na vzorku 233 videozáznamů hlasivek s různým typem a stupněm patologické léze, u kterých byla vždy úspěšně detekována oblast hlasivkové štěrbiny. U hlasivek s velkým stupněm poškození, kde téměř nedocházelo k pohybu nebo byly hlasivkové řasy příliš zdeformované, nelze tuto metodu, a pravděpodobně ani žádnou jinou automatickou metodu, použít.

Pro hodnocení přesnosti odhadu hlasivkové osy byla použita metoda testování shody dvou přímek AxisConformity (AC), tj. v našem případě odhadované hlasivkové osy a anatomické osy určené lékařem ORL (obr. 5). Pro parametr shody AC pak platí:

kde:

k  …koeficient tolerance (k = 0,2)

p …koeficient penalizace úhlu (p = 3)

d_i  …normovaná vzdálenost bodů

h …výška výřezu

x_i …x-souřadnice bodu odhadované osy

x_orli …x-souřadnice bodu anatomické osy podle otorinolaryngologa.

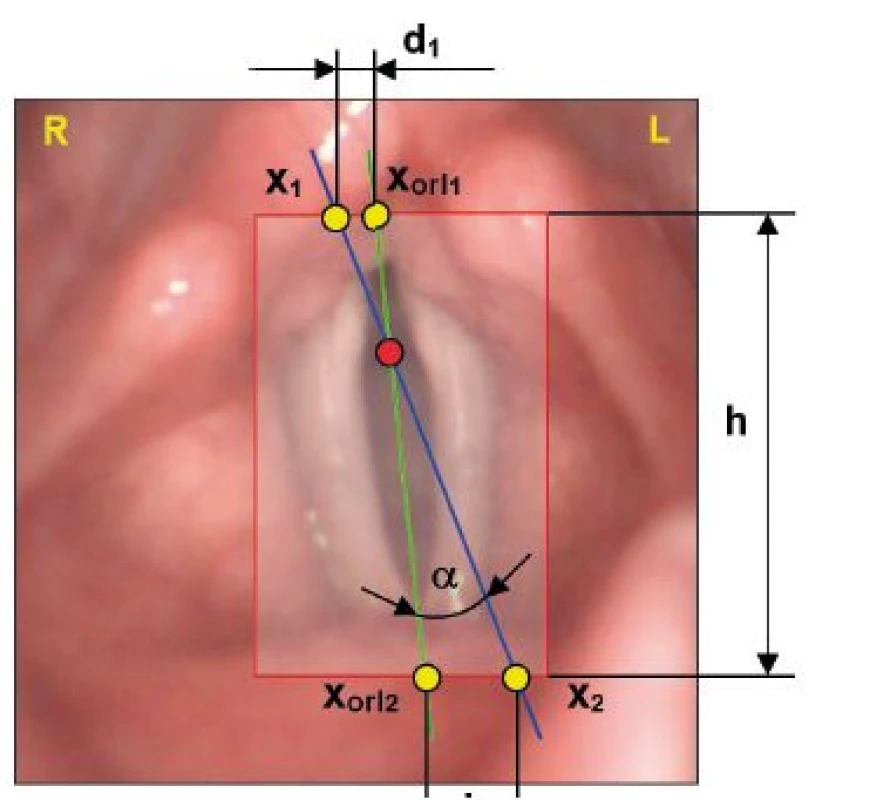
Interval hodnot AC ∈ (0, 1> byl rozdělen na 10 disjunktních podintervalů. Potom kvantovací koeficient q = 0,10. Výsledek přiřazení jednotlivých videozáznamů podle hodnot AC do jednotlivých podintervalů, tj. četností výskytu hodnot AC v testovaném vzorku videozáznamů, je prezentován v tabulce 1.

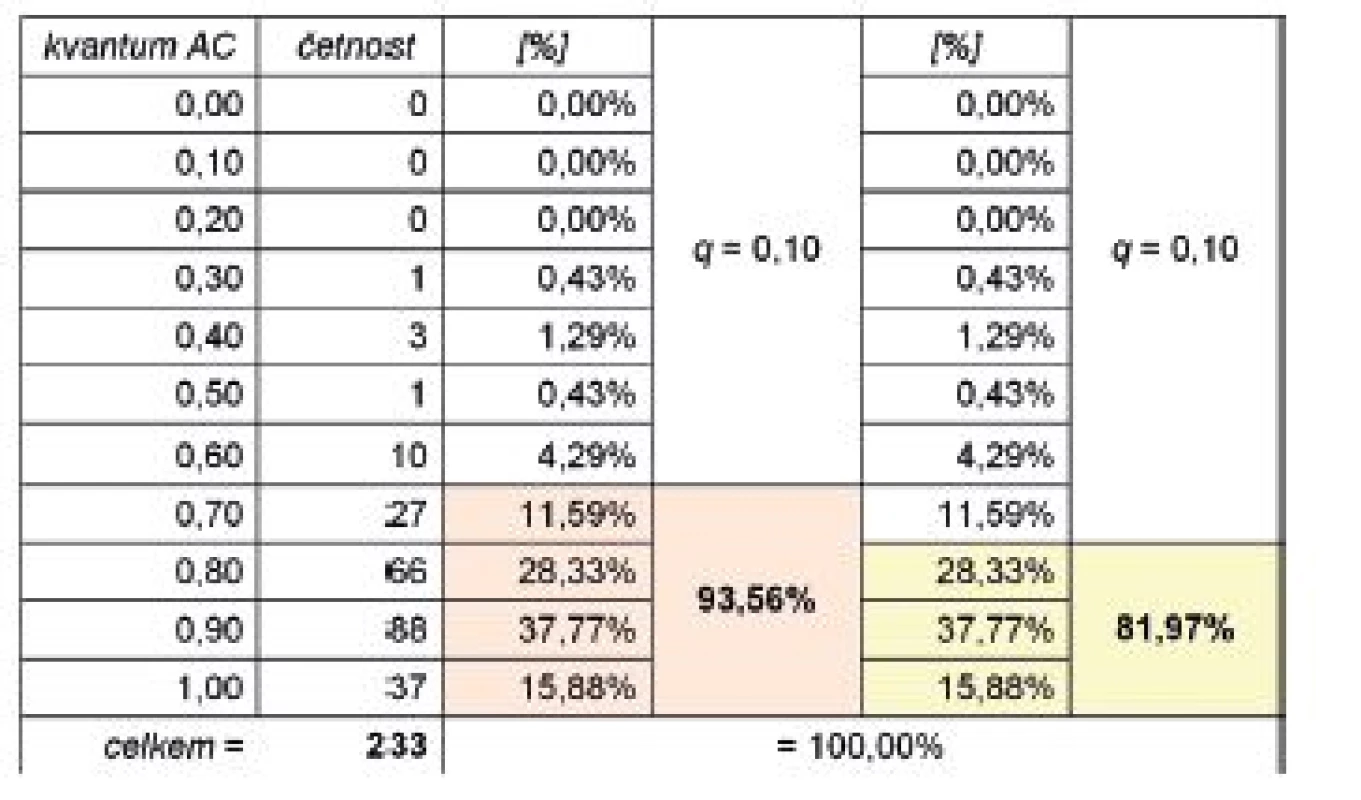
U 233 testovaných videozáznamů se vyskytuje 81,97 % hodnot AC v podintervalech označených { 0,8; 0,9; 1,0 }, reálně se jedná o hodnoty AC ∈ (0,75; 1,00> (tab. 1). To v případě simulací hodnot AC (h = 100px, d_axis = 0px) představuje chybu odhadu v natočení osy |α| < 3,4° a pro simulaci AC (h = 100px, α = 0°) je chyba odhadu polohy |d_axis|< 3px. Zahrneme-li do hodnocení také podinterval { 0,7 }, tj. reálně AC ∈ (0,65; 1,00) (tab. 1), pak do tohoto intervalu hodnot AC patří 3,56 % testovaných os. Pro simulaci hodnot AC (h = 100px, d_axis = 0px) se jedná o chybu odhadu natočení |α|< 5,7° a pro simulaci AC (h = 100px, α = 0°) je chyba odhadu polohy |d_axis|< 5px.

4. PARAMETRY HLASIVKOVÉ ŠTĚRBINY

Počáteční množinu parametrů hlasivkové štěrbiny jsme volili redundantní, tj. obsahuje i takové parametry, které jsou jak přímo měřené, tak odvozované nebo závislé. Další parametry jsou získané na základě aproximace (modelu) hlasivkové štěrbiny nebo sledováním osové symetrie.

Parametry můžeme rozdělit podle jejich typu, způsobu výpočtu a charakteristiky na parametry:

• statické odvozené z jednoho snímku hlasivek
• dynamické vývoj štěrbiny v čase, tj. pro posloupnost snímků
• perioda jeden kmit hlasivek
• videosekvence definovaný počet kmitů hlasivek

a podle typu

• rozměr plocha A a obvod P hlasivkové štěrbiny
• tvar členitost a podlouhlost hlasivkové štěrbiny
• symetrie parametry vztažené k hlavní ose Axis a její normále Norm
• těžiště parametry počítané vzhledem k plošnému těžišti C_k štěrbiny
• elipsa parametry odvozené od aproximace štěrbiny elipsou
• kymogram

V následujícím jsou uvedeny detaily vybrané skupiny parametrů symetrie a těžiště, které jsou bezprostředně závislé na kvalitě odhadu osy symetrie hlasivek. Na jednotlivých kazuistikách prezentujeme schopnost parametrů odlišit anomální chování hlasivky.

4.1  Parametry symetrie

Jedná se o soubor parametrů, které se odvíjejí od definované osy symetrie hlasivek Axis, viz kap. 3, a normály Norm. Normála je úsečka kolmá k hlavní ose hlasivek, jejíž krajní body jsou body vnitřní hranice H_k štěrbiny S_k, a která protíná hlavní osu v jejím středu. Použití těchto parametrů má význam pro analýzu dynamiky jak jednoho celého kmitu hlasivek, tak videosekvence snímků HSV.

Symetrie plochy

Pro posouzení symetrie hlasivek podle plochy štěrbiny je nutné definovat vzhledem k hlavní ose Axis plochu levé části A_left(k) a pravé části A_right(k) hlasivkové štěrbiny S_k ve snímku k a parametr vychýlení plochy A_delt(k).

A_delt(k) = A_right(k) – A_left(k). (4)

Příklady vývoje rozměrového parametru celkové plochy hlasivkové štěrbiny A a současně parametrů symetrie podle plochy A_right, A_left a A_delt pro videosekvenci 100 snímků zdravého jedince a pacienta s levostrannou parézou zvratného nervu jsou na obrázku 6. Z uvedených grafů je patrný rozdíl ve vývoji parametrů symetrie. U zdravého jedince se plochy pravé a levé části hlasivkové štěrbiny shodují, viz také vývoj A_delt kolem nulové hodnoty. Naopak u pacienta s levostrannou parézou zvratného nervu je plocha levé části hlasivkové štěrbiny v jednotlivých snímcích videosekvence výrazně menší než plocha pravé části, viz také vývoj parametru A_delt. V obou případech ale vývoj celkové plochy A hlasivkové štěrbiny nevykazuje žádné výrazné odlišnosti. V případě levostranné parézy jen nedochází k úplnému uzavření hlasivkové štěrbiny, což ale nemusí být diagnosticky významné.

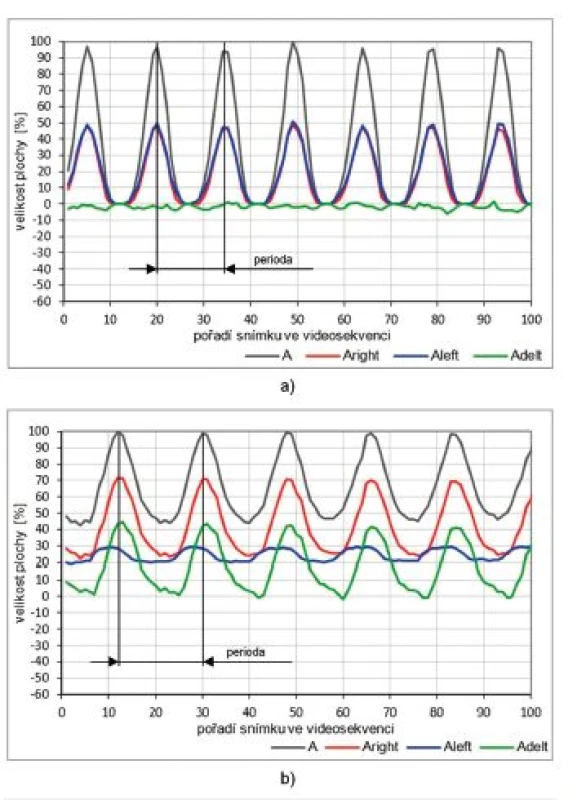
Symetrie obvodu

V tomto případě definujeme vzhledem k hlavní ose Axis obvod levé části P_left(k) a pravé části P_right(k) hlasivkové štěrbiny S_k ve snímku k a parametr nesymetrie obvodu hlasivkové štěrbiny P_delt(k). Parametr symetrie obvodu je schopný podchytit takové rozdíly v chování hlasivek, které nemusíme detekovat parametrem symetrie plochy A. Příkladem může být zvlnění okraje levé nebo pravé části štěrbiny S_k, které může vyvolat změnu obvodu P_left(k) nebo P_right(k) při zachování velikosti plochy A_left(k) nebo A_right(k).

P_delt(k) = P_right(k) – P_left(k). (5)

Příklady vývoje rozměrového parametru celkového obvodu hlasivkové štěrbiny P a současně parametrů symetrie podle obvodu P_right, P_left a P_delt pro 100 snímků ve videosekvenci zdravého jedince a pacienta s levostrannou parézou zvratného nervu jsou na obrázku 7. Již v případě vývoje parametru celkového obvodu P je patrný rozdíl ve tvaru křivky, kdy nepravidelnosti, viz obr. 7b, odpovídají změnám členitosti, např. zvlnění, hraniční čáry štěrbiny.

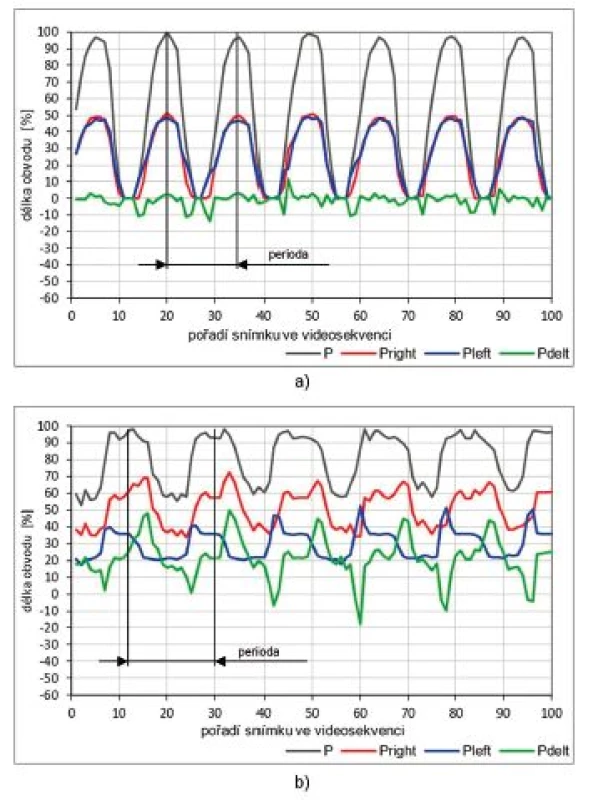
Tyto změny v členitosti jsou typické pro zakmitávání hlasivkové řasy u parézy zvratného nervu. Vývoj obou parametrů P_right, P_left u zdravého jedince je téměř shodný bez známek zakmitávání a odpovídá vývoji parametrů A_left nebo A_right, viz obr. 6a., resp. parametrů A a P. Hodnoty P_delt jsou pak také blízké nulové hodnotě.

Jev zakmitávání hlasivkových řas se ale výrazně projevuje v parametrech P_right a P_left u parézy zvratného nervu. Parametr P_delt, viz obr. 7b, ukazuje na nesymetrii v kinematice hlasivkové štěrbiny vzhledem k ose symetrie. Také průběh parametru celkového obvodu hlasivkové štěrbiny P se podstatně liší od průběhu parametru celkové plochy A právě vlivem zakmitávání hlasivkových řas.

4.2  Parametry těžiště

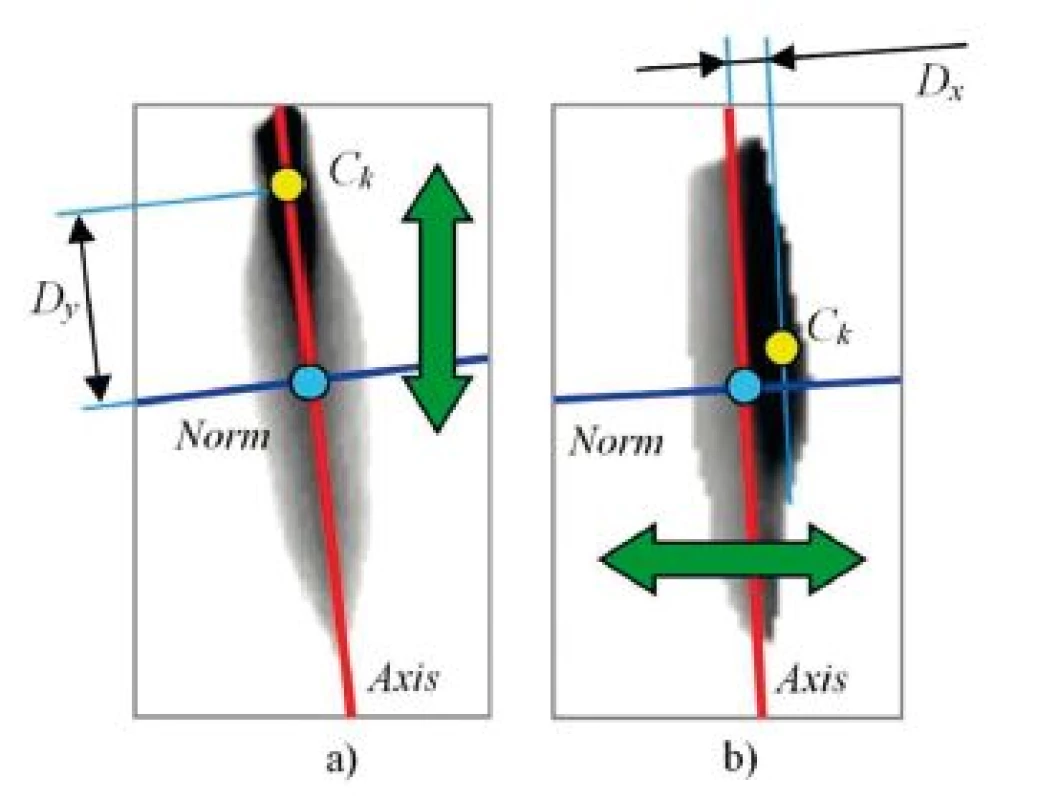
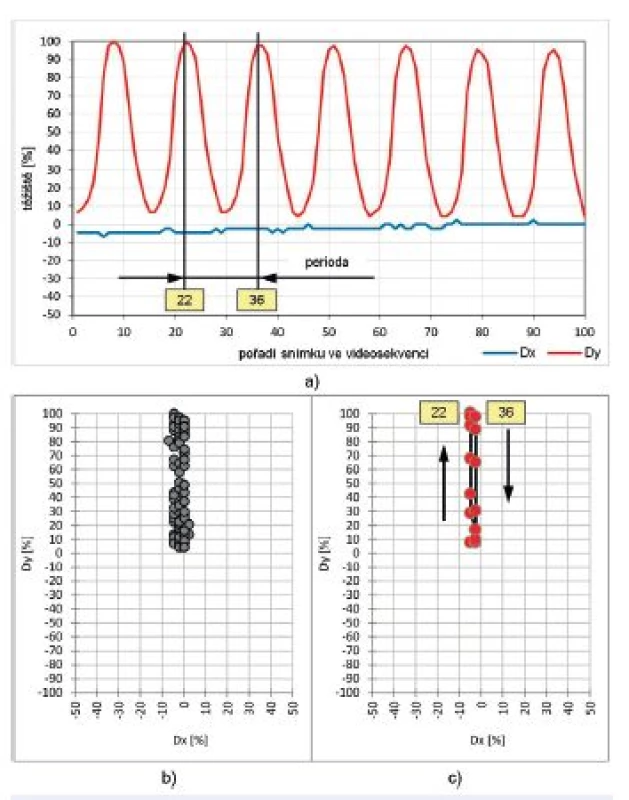
Parametry těžiště budeme chápat jako vzdálenost plošného těžiště štěrbiny S_k ve snímku k od hlavní osy hlasivek D_x a její normály D_y. Svým charakterem se jedná o parametry jak statické tak dynamické. Význam sledování dynamiky vývoje těžiště je patrný ze schematického zobrazení na obrázku 8 a výsledků analýzy symetrické a nesymetrické hlasivky, obrázky 9 a 10.

Pro výpočet polohy těžiště C_k(x_c, y_c) platí následující vztahy:

kde x a y jsou hodnoty jednotlivých souřadnic obrazových bodů, které tvoří segmentovanou oblast štěrbiny S_k, detekovanou metodami, viz kap. 2.

Na obrázku 9 jsou prezentovány výsledky analýzy pohybu těžiště hlasivkové štěrbiny symetrické hlasivky u zdravého jedince. Dominantní pohyb je ve směru D_y, tj. podél osy symetrie štěrbiny. Maximální vychýlení těžiště je ve směru D_y (43 px  100%). Maximální vychýlení ve směru D_x, tj. normály, jsou 2 px (= 4,65% max. vychýlení těžiště).

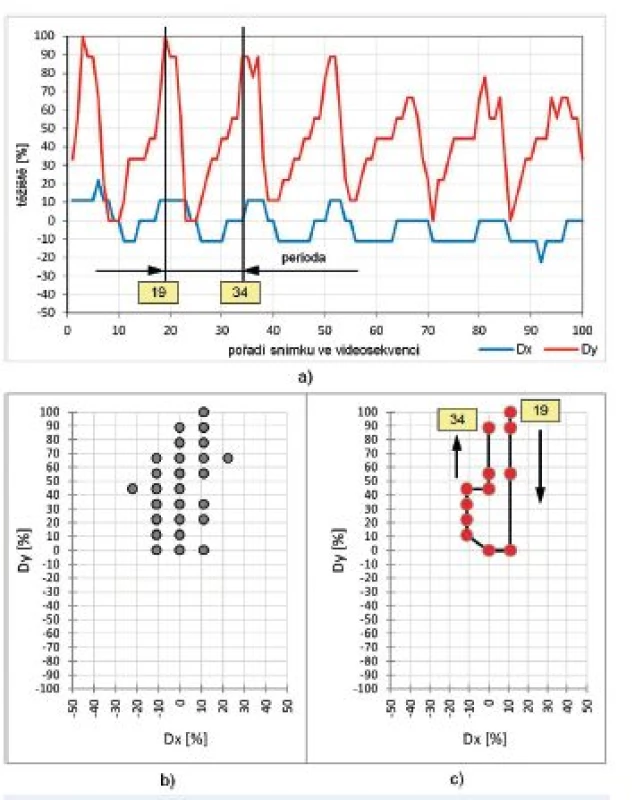
Analýza (obr. 10) ukazuje změnu v pohybu těžiště v případě karcinomu na hlasivce vlevo. Dominantní je stále pohyb ve směru D_y s maximálním vychýlením těžiště 9 px (= 100%). Malý počet obrazových bodů [ px ] je způsoben větší vzdáleností kamery od hlasivek. Pohyb Dx ve směru normály jsou pak 2 px (= 22,22% max. vychýlení těžiště).

5. ZÁVĚR

Při hodnocení kinematiky hlasivek z videozáznamu vysokorychlostní kamerou bylo nutné nejprve vyřešit dvě základní úlohy. V jednotlivých snímcích detekovat hlasivkovou štěrbinu, určit hranici hlasivkové štěrbiny a provést odhad její osy symetrie. K řešení těchto úloh jsme aplikovali metody Signal Processing, spec. Image Processing. Úspěšnost detekce hlasivkové štěrbiny a odhadu osy symetrie byla testována na 233 videozáznamech. Bylo ověřeno, že osa symetrie je odhadována v porovnání se subjektivním hodnocením velmi přesně, v 82 % případů byl odhad osy symetrie v intervalu chyby posunutí do ± 3px a úhlu natočení do ± 3,4°. Tím byla také potvrzena přesnost primární informace, tj. detekce hlasivkové štěrbiny a její hranice.

Úspěšné vyřešení tohoto problému nám dále umožnilo definovat takové parametry, které jsou odvozené od osy symetrie a určitým způsobem charakterizují hlasivkovou štěrbinu a její dynamiku. Z množiny používaných parametrů jsme pro představení navrhovaného řešení problému vybrali ty, které vyjadřují symetrii hlasivkové štěrbiny a dále jsme soustředili pozornost na sledování pohybu jejího těžiště. Ukázalo se, že takto navržené metody mohou odhalit některé nepravidelnosti v pohybu hlasivek, které jsou při běžném pozorování videozáznamu špatně postřehnutelné. To je patrné z uvedeného příkladu dvou diagnóz, parézy zvratného nervu a karcinomu, na nichž jsou prezentovány výsledky vývoje parametrů. Z doposud získaných zkušeností a analýzy dat pro omezený počet videozáznamů a diagnóz odvozujeme, že parametry symetrie a polohy těžiště bude účelné zařadit do již existujícího souboru parametrů, které testujeme pro použití při hodnocení chování hlasivek, kvality závěru glottis a kinematiky hlasivek (5, 13, 14, 17). Cílem je vytvořit kombinovaný nástroj použitelný jako podporu včasné diagnostiky závažných onemocnění hlasivek. Tento nástroj je postupně doplňován a testován. Principem je nalezení takového chování hlasivek, které je nepravidelné, nahodilé a nestandardní v rámci provedeného vyšetření (8) a které je běžnými technikami obtížně detekovatelné.

Aplikace navržených parametrů a metod má i svá úskalí. Spolehlivost a přesnost parametrů symetrie a polohy těžiště jsou závislé na kvalitě videozáznamu, tj. na velikosti detailu hlasivek v počtu obrazových bodů, na úhlu, pod kterým byly hlasivky snímány, na zaostření kamery a stabilitě videozáznamu. To je ovlivněno jak lidským faktorem během vyšetření, tak obecněji dostupným technickým vybavením.

Adresa ke korespondenci:

Ing. Jiří Pešta, CSc.

ORL klinika FN Plzeň

Tř. dr. E. Beneše 13

305 99 Plzeň

e-mail: pestaj@fnplzen.cz