-
Články
- Časopisy
- Kurzy
- Témy
- Kongresy
- Videa
- Podcasty
Improved Detection of Common Variants Associated with Schizophrenia and Bipolar Disorder Using Pleiotropy-Informed Conditional False Discovery Rate
Several lines of evidence suggest that genome-wide association studies (GWAS) have the potential to explain more of the “missing heritability” of common complex phenotypes. However, reliable methods to identify a larger proportion of single nucleotide polymorphisms (SNPs) that impact disease risk are currently lacking. Here, we use a genetic pleiotropy-informed conditional false discovery rate (FDR) method on GWAS summary statistics data to identify new loci associated with schizophrenia (SCZ) and bipolar disorders (BD), two highly heritable disorders with significant missing heritability. Epidemiological and clinical evidence suggest similar disease characteristics and overlapping genes between SCZ and BD. Here, we computed conditional Q–Q curves of data from the Psychiatric Genome Consortium (SCZ; n = 9,379 cases and n = 7,736 controls; BD: n = 6,990 cases and n = 4,820 controls) to show enrichment of SNPs associated with SCZ as a function of association with BD and vice versa with a corresponding reduction in FDR. Applying the conditional FDR method, we identified 58 loci associated with SCZ and 35 loci associated with BD below the conditional FDR level of 0.05. Of these, 14 loci were associated with both SCZ and BD (conjunction FDR). Together, these findings show the feasibility of genetic pleiotropy-informed methods to improve gene discovery in SCZ and BD and indicate overlapping genetic mechanisms between these two disorders.
Published in the journal: Improved Detection of Common Variants Associated with Schizophrenia and Bipolar Disorder Using Pleiotropy-Informed Conditional False Discovery Rate. PLoS Genet 9(4): e32767. doi:10.1371/journal.pgen.1003455
Category: Research Article
doi: https://doi.org/10.1371/journal.pgen.1003455Summary
Several lines of evidence suggest that genome-wide association studies (GWAS) have the potential to explain more of the “missing heritability” of common complex phenotypes. However, reliable methods to identify a larger proportion of single nucleotide polymorphisms (SNPs) that impact disease risk are currently lacking. Here, we use a genetic pleiotropy-informed conditional false discovery rate (FDR) method on GWAS summary statistics data to identify new loci associated with schizophrenia (SCZ) and bipolar disorders (BD), two highly heritable disorders with significant missing heritability. Epidemiological and clinical evidence suggest similar disease characteristics and overlapping genes between SCZ and BD. Here, we computed conditional Q–Q curves of data from the Psychiatric Genome Consortium (SCZ; n = 9,379 cases and n = 7,736 controls; BD: n = 6,990 cases and n = 4,820 controls) to show enrichment of SNPs associated with SCZ as a function of association with BD and vice versa with a corresponding reduction in FDR. Applying the conditional FDR method, we identified 58 loci associated with SCZ and 35 loci associated with BD below the conditional FDR level of 0.05. Of these, 14 loci were associated with both SCZ and BD (conjunction FDR). Together, these findings show the feasibility of genetic pleiotropy-informed methods to improve gene discovery in SCZ and BD and indicate overlapping genetic mechanisms between these two disorders.
Introduction
Converging evidence suggests that complex human phenotypes are influenced by numerous genes each explaining a small proportion of the variance [1]. Though thousands of single nucleotide polymorphisms (SNPs) have been identified by genome-wide association studies (GWAS) [2], [3], these SNPs fail to explain a large proportion of the heritability of most complex phenotypes studied. This is commonly referred to as the ‘missing heritability’ problem. Recent findings indicate that GWAS have the potential to explain a greater proportion of the heritability of common complex phenotypes [4]–[6], and more SNPs are likely to be identified in larger samples [7]. Due to the polygenic nature of most complex traits and disorders, a large number of SNPs are likely to have associations too small in magnitude to be identified with currently available sample sizes [8]. New analytical methods are therefore needed to reliably identify a larger proportion of SNPs associated with complex diseases and phenotypes, since recruitment and genotyping of sufficiently large samples for existing methods may be impractical and prohibitively expensive. Genetic pleiotropy is defined as a single gene or variant being associated with more than one distinct phenotype. In the present study we use a new genetic pleiotropy-informed approach for GWAS to capture more of the polygenic effects in complex phenotypes. Given the high number of traits in humans, and the relatively small number of genes (∼20,000), some genes have to affect multiple traits (genetic pleiotropy) [10]. By combining independent GWAS from associated disorders, we hypothesize that for disorders with related etiologies a genetic pleiotropy-informed approach can significantly improve gene discovery and help capture more of the missing heritability.
Recent findings suggest overlapping SNPs between several human traits [9], [11] and disorders [12]–[14]. To date, methods to assess this genetic pleiotropy have not taken full advantage of the existing GWAS data and the majority of studies have focused on the subset of SNPs exceeding a Bonferroni-corrected threshold of significance for each trait or disorder [12]–[14]. However, this approach cannot detect SNPs that only reach genome-wide significance in the combined analysis but do not meet Bonferroni-corrected significance in the individual phenotype (hereafter referred to as polygenic pleiotropy). Combining GWAS statistics from two disorders also provides increased power to discover genes associated with common biological mechanisms, and thus inform on overlapping pathophysiological relationships between the disorders. In the current study, we use a pleiotropy-informed statistical approach to improve gene discovery in schizophrenia and bipolar disorder, two disorders with high heritability [15], where most of the underlying genetic architecture remains unknown [13], [14], despite recent discoveries [13], [14], [16], [17].
Schizophrenia and bipolar disorder share several clinical characteristics [18]–[20], including psychotic symptoms, disorders of thought and impairment of cognitive functions [21]. The disorders are often also treated with similar pharmacological agents [18], [19]. Whether schizophrenia and bipolar disorder should be regarded as separable disease entities or as a single disease with a spectrum of symptoms [18]–[20], as proposed in the continuum hypothesis of psychosis [22], has been much discussed. With the forthcoming revision of the Diagnostic and Statistical Manual of Mental Disorders (DSM), this question has received renewed attention [19], [20], [23]. Both disorders have an estimated heritability of 0.7–0.8, and are regarded as complex disorders with a polygenic architecture. Several lines of evidence have suggested overlapping genetic susceptibility in bipolar disorder and schizophrenia [15], [24]–[26]. Recently, a combined analysis of two large GWAS (16,374 cases and 12,044 controls) revealed three loci (CACNA1C, rs4765905, p = 7.0×10−9, ANK3 rs10994359, p = 2.5×10−8, ITIH3/4 region rs2239547, p = 7.8×10−9) significantly associated with both disorders (Fisher's combined p in combined samples) [13], [14]. Still, given the high degree of heritability and large similarities in clinical phenotypes, there are likely several more undiscovered overlapping genetic factors.
Here, using summary statistics from two independent large GWAS, we applied a model-free statistical analysis method to identify SNPs exhibiting pleiotropic relationships between schizophrenia and bipolar disorder. First, we separated out the common controls in the bipolar disorder and schizophrenia samples [13], [14], ensuring non-overlapping samples. After applying genomic inflation control, we computed the conditional empirical cumulative distribution functions (cdfs) of the corrected p-values. Empirical cdfs for schizophrenia SNP p-values were determined conditional on the significance of the corresponding nominal p-values in bipolar disorder, and vice versa. For each nominal p-value, an estimate of the conditional False Discovery Rate (FDR) was obtained from the conditional empirical cdfs [5]. Using this conditional FDR method, we constructed two-dimensional FDR “look-up” tables, with FDR in schizophrenia SNPs computed conditional on nominal bipolar disorder p-values, and vice versa. Using these tables we identified 58 loci associated with schizophrenia and 35 loci associated with bipolar disorder at a conditional FDR level of 0.05. We used a conjunction method to investigate SNPs significantly associated with both schizophrenia and bipolar disorder. Specifically, we computed the conditional FDR for schizophrenia given bipolar disorder nominal p-values, and conditional FDR for bipolar disorder given schizophrenia nominal p-values, and took the maximum of both values as the conjunction FDR. With this approach we identified 14 pleiotropic loci indicating several overlapping genetic risk factors for the two disorders. Finally, using mixture model-based analyses we estimated the proportion and distribution of non-null SNPs, demonstrating that the large increase in power from using conditional vs. unconditional FDR methods is derived from the high polygenicity of both phenotypes with many test statistics just below significance thresholds, and the largely overlapping distribution (high degree of pleiotropy) of non-null SNPs for schizophrenia and bipolar disorder.
Results
Q–Q plots of schizophrenia SNPs conditional on association with bipolar disorder and vice versa
Under large-scale testing paradigms, such as GWAS, quantitative estimates of likely true associations can be estimated from distributions of summary statistics [27], [28]. A common method for visualizing the ‘enrichment’ of statistical association relative to that expected under the global null hypothesis is through Q-Q plots of nominal p-values obtained from GWAS summary statistics. The usual Q-Q curve has the nominal p-value, denoted by “p”, as the y-ordinate and the corresponding value of the empirical cdf, here denoted by “q,” as the x-ordinate. Under the global null hypothesis the theoretical distribution is uniform on the interval [0,1]. As is common in GWAS, we instead plot −log10 p against −log10 q to emphasize tail probabilities of the theoretical and empirical distributions. As such, genetic ‘enrichment’ refers to a leftward shift in the Q-Q curve, corresponding to a larger fraction of SNPs with nominal −log10 p-value greater than or equal to a given threshold. Conditional Q-Q plots are formed by creating subsets of SNPs based on values of an additional variable (auxiliary measure) for each SNP, and computing Q-Q plots separately for each subset of SNPs. If SNP enrichment is captured by variation in the auxiliary measure, this is expressed as successive leftward deflections in conditional Q-Q plots as values of the additional variable increase.
Conditional Q-Q plots for schizophrenia given nominal p-values of association with bipolar disorder (SCZ|BD; Figure 1A) show enrichment across different levels of significance for bipolar disorder. The earlier departure from the null line (leftward shift) suggests a greater proportion of true associations for a given nominal schizophrenia p-value. Successive leftward shifts for decreasing nominal bipolar disorder p-value thresholds indicate that the proportion of non-null effects in schizophrenia varies considerably across different levels of association with bipolar disorder. For example, the proportion of SNPs in the −log10(pBD) ≥3 category reaching a given significance level for schizophrenia (e.g., −log10(pSCZ) ≥4) is roughly 50 times greater than for the −log10(pBD) ≥0 category (all SNPs), indicating a high level of enrichment. An even stronger pleiotropic enrichment can be seen for bipolar disorder conditioned on nominal p-values of association with schizophrenia (BD|SCZ; Figure 1B), Here, the proportion of SNPs in the −log10(pSCZ) ≥3 category reaching a given significance level for bipolar disorder (e.g., −log10(pBD)≥4) is roughly 500 times greater than for the −log10(pSCZ)≥0 category (all SNPs), indicating a very high level of enrichment.
Fig. 1. Stratified Q–Q plot and Stratified True Discovery Rate plots. 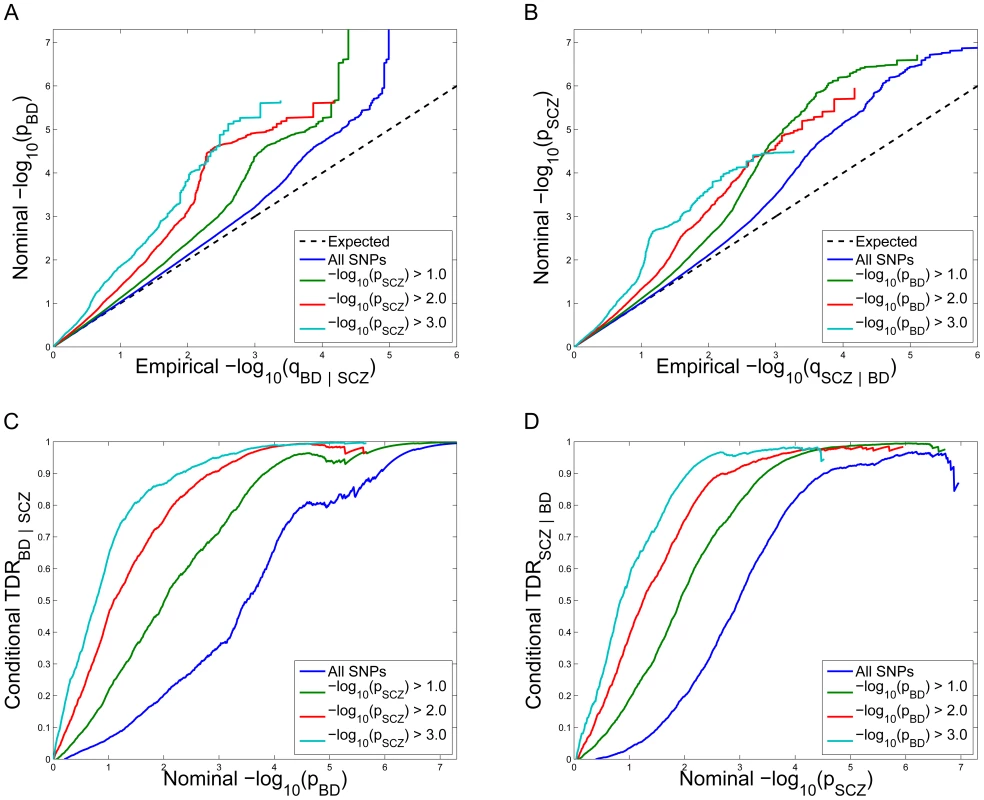
Upper panel: Stratified Q-Q plot of nominal versus empirical −log10 p-values (corrected for inflation) in A) schizophrenia (SCZ) below the standard GWAS threshold of p<5×10−8 as a function of significance of the association with bipolar disorder (BD) at the level of −log10(p)>0, −log10(p)>1, −log10(p)>2, −log10(p)>3 corresponding to p<1, p<0.1, p<0.01, p<0.001, respectively, and in B) BD below the standard GWAS threshold of p<5×10−8 as a function of significance of association with SCZ at the level of −log10(p)>0, −log10(p)>1, −log10(p)>2, −log10(p)>3 corresponding to p<1, p<0.1, p<0.01, p<0.001, respectively. Dotted lines indicate the null-hypothesis. Lower panel: Stratified True Discovery Rate (TDR) plots illustrating the increase in TDR associated with increased pleiotropic enrichment in C) SCZ conditional on nominal BD p-values (SCZ|BD), and D) BD conditional on nominal SCZ p-values (BD|SCZ). For more information about QQ plots, see Text S1. Conditional True Discovery Rate (TDR) in schizophrenia is increased by bipolar disorder, and vice versa
Since categories of SNPs with stronger pleiotropic enrichment are more likely to be associated with schizophrenia, to maximize power for discovery all tag SNPs should not be treated exchangeably. Specifically, variation in enrichment across pleiotropic categories is expected to be associated with corresponding variation in the TDR (equivalent to 1-FDR) [29] for association of SNPs with schizophrenia. A conservative estimate of the TDR for each nominal p-value is equivalent to 1 – (p/q), easily read off from conditional Q-Q plots (see Material and Methods). This relationship is shown for schizophrenia conditioned on nominal bipolar disorder p-values (SCZ|BD; Figure 1C) and bipolar disorder conditioned on nominal schizophrenia p-values (BD|SCZ; Figure 1D). For a given conditional TDR the corresponding estimated nominal p-value threshold varies with a factor of 100 from the most to the least enriched SNP category for schizophrenia conditioned on bipolar disorder (SCZ|BD), and approximately a factor of 500 for bipolar disorder conditioned on schizophrenia (BD|SCZ).
Schizophrenia gene loci identified with conditional FDR
We constructed a “conditional” Manhattan plot for schizophrenia showing the FDR conditional on bipolar disorder (Figure 2) and identified significant loci on a total of 18 chromosomes (1–4, 6–16, 18, 20 and 22) associated with schizophrenia leveraging the reduced FDR obtained by the associated bipolar disorder phenotype. To estimate the number of independent loci, we ‘pruned’ the associated SNPs (removed SNPs with linkage disequilibrium (LD)>0.2), and identified a total of 58 independent loci with a significance threshold of conditional FDR<0.05 (Table 1). Using the more conservative conditional FDR threshold of 0.01, 9 independent loci remained significant. One locus was located in the HLA region on chromosome 6. Of note, using a standard Bonferroni-corrected approach, no loci would have been discovered. Using the FDR method in schizophrenia alone, 4 loci were identified. Of these, the regions close to TRIM26 (6p21.3), MMP16 (8q21.3) and NT5C2 (10q24.32) have been identified in earlier GWAS studies after including large replication samples [13]. The remaining loci would not have been identified in the current sample without using the pleiotropy-informed conditional FDR method. Of interest, the VRK2 region (2p16.1) was identified in the previous sample after including a large schizophrenia replication sample [30], and the ITIH4 region (3p21.1), ANK3 (10q21) and CACNA1C (12p13.3) were discovered previously in the same, combined schizophrenia and bipolar disorder sample [13], [14]. Thus, the current pleiotropy-informed FDR method validated 7 loci discovered in considerably larger samples, and discovered 51 new loci.
Fig. 2. “Conditional Manhattan plot” of conditional −log10 (FDR) values for schizophrenia (SCZ) alone (black) and SCZ given bipolar disorder (BD; SCZ|BD, red). 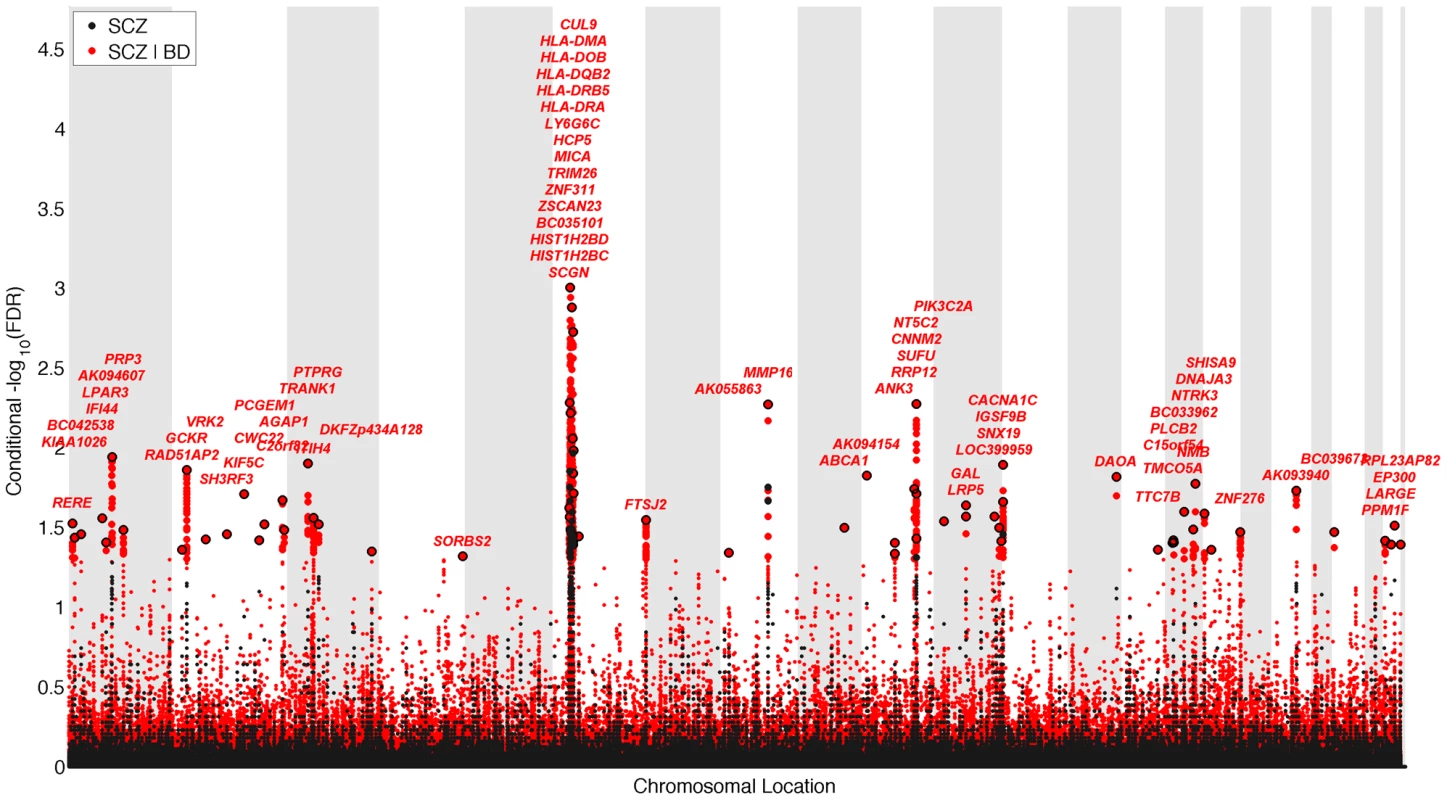
SNPs with conditional −log10 FDR>1.3 (i.e. FDR<0.05) are shown with large points. A black line around the large points indicates the most significant SNP in each LD block and this SNP was annotated with the closest gene, which is listed above the symbols in each locus. The figure shows the localization of significant loci. Details about the loci are provided in Table 1. Tab. 1. Conditional FDR; SCZ loci given BD (SCZ|BD). 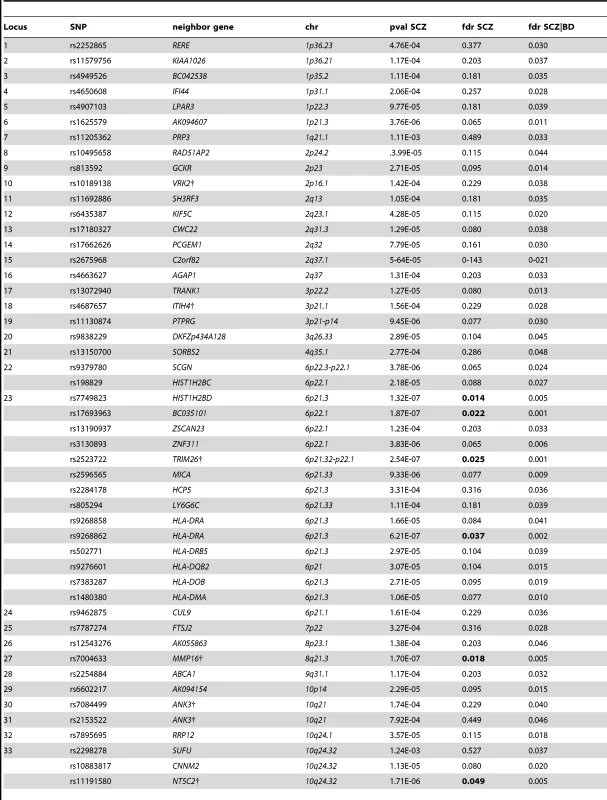
Independent complex or single gene loci (r2<0.2) with SNP(s) with a conditional FDR (condFDR)<0.05 in schizophrenia (SCZ) given the association in bipolar disorder (BD). We defined the most significant SCZ SNP in each LD block based on the minimum condFDR for BD. The most significant SNPs in each LD block are listed. All loci with SNPs with condFDR<0.05 were used to define the number of the loci. Chromosome location (Chr). SCZ FDR values<0.05 are in bold. Bipolar disorder gene loci identified with conditional FDR
We constructed a “conditional” Manhattan plot for bipolar disorder showing the FDR conditional on schizophrenia (Figure 3) and identified significant loci on a total of 16 chromosomes (1–3, 5–8, 10–14, 16 and 19–22) associated with bipolar disorder leveraging the reduced FDR obtained by the associated schizophrenia phenotype. To estimate the number of independent loci, we pruned the associated SNPs (removed SNP with LD >0.2), and identified a total of 35 independent loci with a significance threshold of conditional FDR<0.05 (Table 2). Of these, one locus was complex, i.e. included several significant SNPs, and the rest were single gene loci. Using the more conservative conditional FDR threshold of 0.01, 5 independent loci remained significant. The most significant locus was close to ANK3 on chromosome (10q21). This is the only locus that would have been discovered using standard methods based on p-values (Bonferroni correction). Using the FDR method in bipolar disorder alone, an additional locus was identified, close to CACNA1C (12p13.3). Both these loci have been discovered earlier [14], [31]. The remaining 33 loci would not have been identified in the current sample without using the pleiotropy-informed conditional FDR method. Of these, the regions close to SYNE1 (6q25) and ODZ4 (11q14.1) have been identified in earlier GWAS after including large replication samples [14], [32]. Of interest, the ITIH3 region (3p21.1), ANK3 (10q21) and CACNA1C (12p13.3) were discovered previously in the same, combined schizophrenia and bipolar disorder sample [13], [14]. Thus, pleiotropy-informed conditional FDR validated 5 loci discovered in considerably larger samples, and discovered 30 new loci.
Fig. 3. “Conditional Manhattan plot” of conditional −log10 (FDR) values for Bipolar disorder (BD) alone (black) and BD given schizophrenia (SCZ; BD|SCZ, blue). 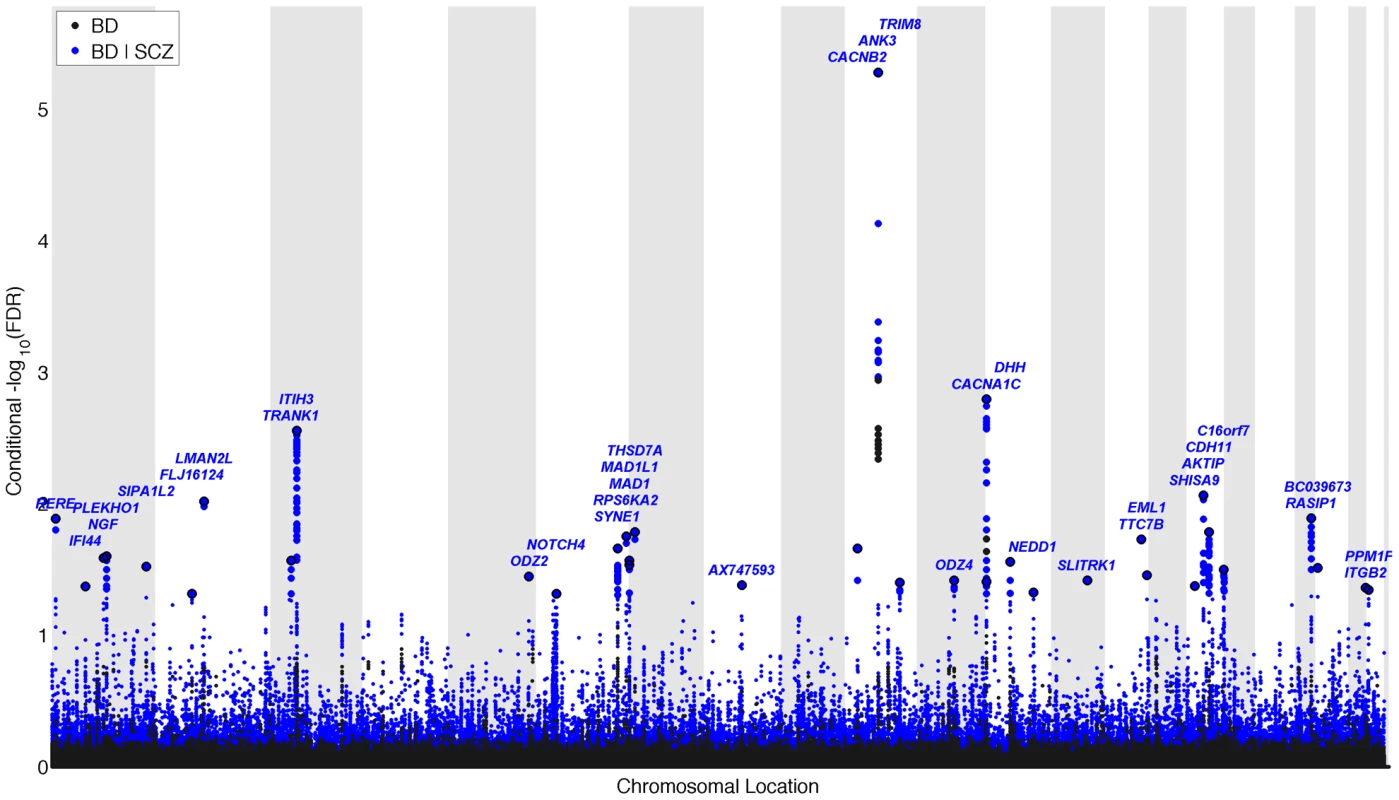
SNPs with conditional −log10 FDR>1.3 (i.e. FDR<0.05) are shown with large points. A black line around the large points indicates the most significant SNP in each LD block and this SNP was annotated with the closest gene, which is listed above the symbols in each locus. The figure shows the localization of significant loci. Details about the loci are provided in Table 2. Tab. 2. Conditional FDR; BD loci given SCZ (BD|SCZ). 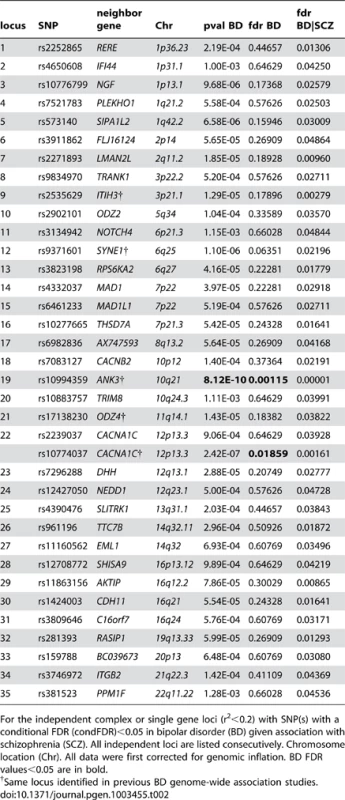
For the independent complex or single gene loci (r2<0.2) with SNP(s) with a conditional FDR (condFDR)<0.05 in bipolar disorder (BD) given association with schizophrenia (SCZ). All independent loci are listed consecutively. Chromosome location (Chr). All data were first corrected for genomic inflation. BD FDR values<0.05 are in bold. Pleiotropic gene loci in both schizophrenia and bipolar disorder identified with conjunctional FDR
To identify pleiotropic loci in schizophrenia and bipolar disorder, we performed a conjunction FDR analysis, using this to construct a “conjunction” Manhattan plot (Figure 4). We detected 14 independent pleiotropic loci (pruned based on LD>0.2, black line around large circles) with conjunction FDR<0.05, all single gene loci, located on a total of 10 chromosomes (chr. 1, 3, 6, 7, 10, 12, 14, 16, 20, 22 – for further details, please see Table 3). Of these loci, 3 have been implicated in bipolar disorder and schizophrenia earlier: NOTCH4 (6p21.2) with schizophrenia using a larger replication sample [13], [17], and the ITIH4 (3p21.1), and CACNA1C (12p13.3) regions, both discovered previously in the same, combined schizophrenia and bipolar disorder sample [13], [14]. Interestingly only one conjunctional locus was found on chromosome 6, suggesting that there are several schizophrenia loci on this chromosome not overlapping with bipolar disorder. The ANK3 locus was not indicated in the conjunctional analysis, which indicates that the overlap is mostly driven by the association in bipolar disorder (Table 2). The direction of the effect (z-scores) across all the pleiotropic SNPs was the same for bipolar disorder and schizophrenia, except for locus 33 (BC039673, 20p13), which could be due to differences in LD structure in this region. These findings suggest overlapping genetic pathways in schizophrenia and bipolar disorders.
Fig. 4. “Conjunction Manhattan plot” of conjunction −log10 (FDR) values for schizophrenia (SCZ) and bipolar disorder (BD). 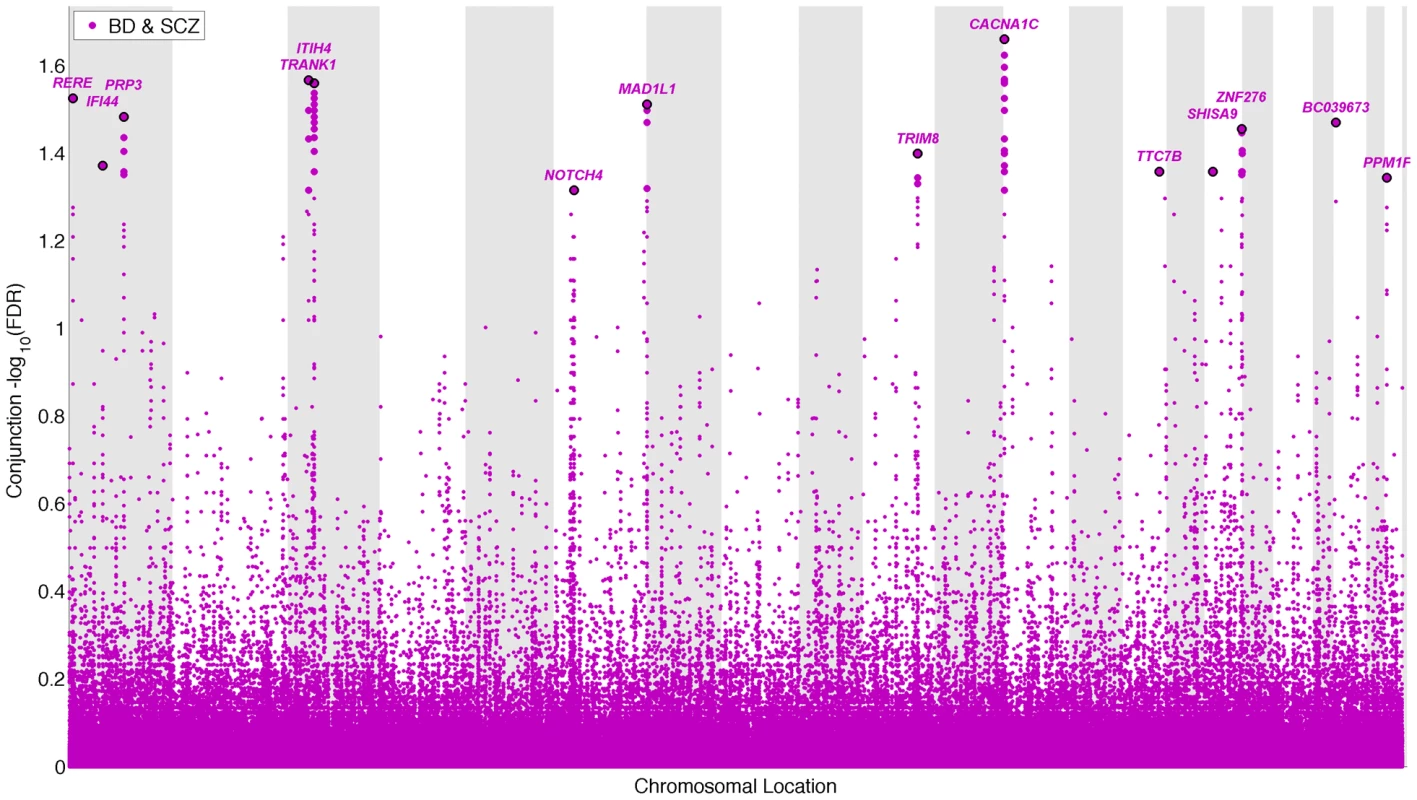
SNPs with −log10 (FDR)>1.3, (i.e. FDR<0.05) for both SCZ and BD are shown with large points. A black line around the large points indicates the most significant SNP in each LD block and this SNP was annotated with the closest gene, which is listed above the symbols in each chromosome. The figure shows the localization of the ‘pleiotropic loci’, and further details are provided in Table 3. Tab. 3. Conjunction FDR; pleiotropic loci in SCZ and BD (SCZ&BD). 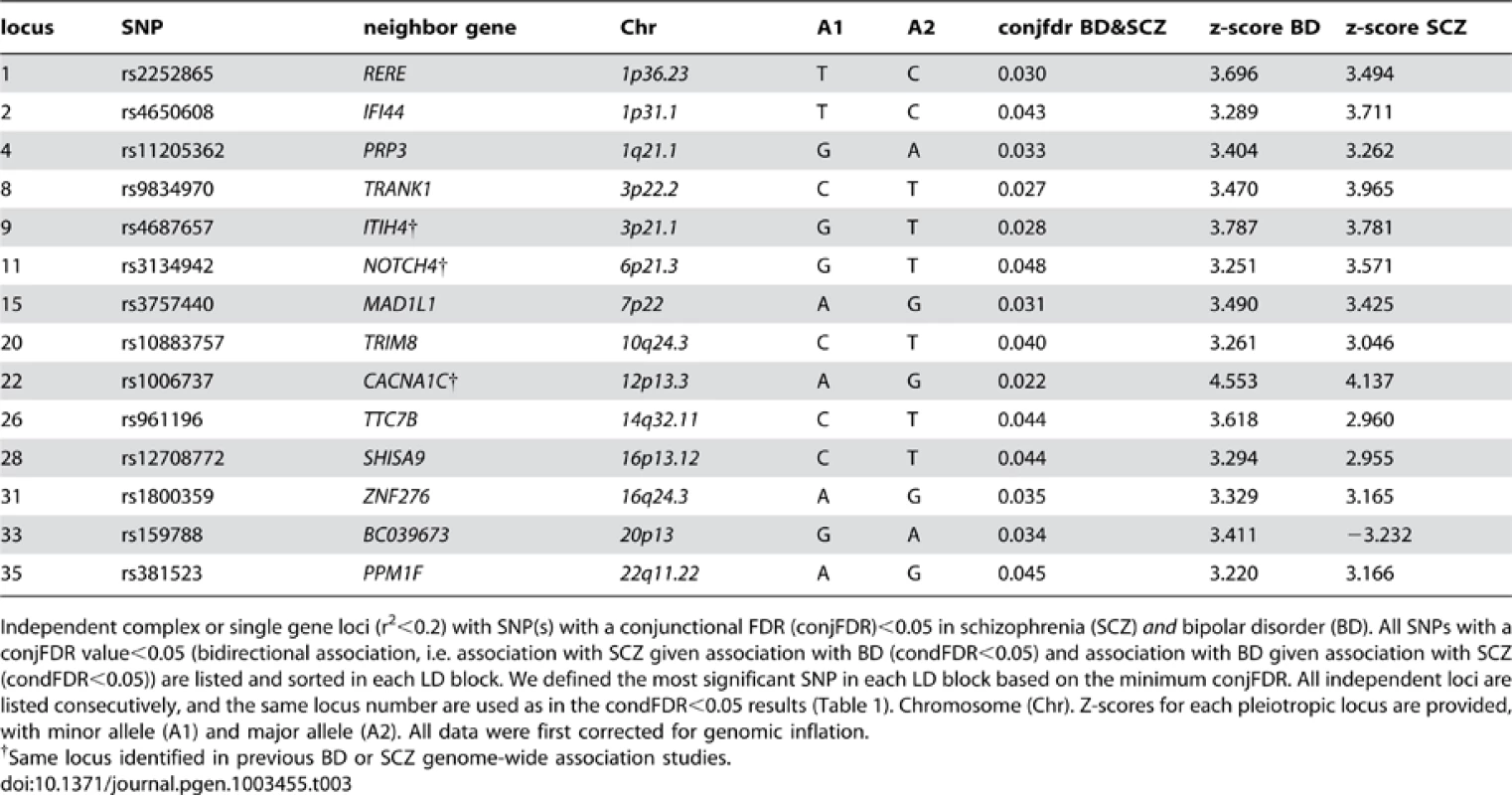
Independent complex or single gene loci (r2<0.2) with SNP(s) with a conjunctional FDR (conjFDR)<0.05 in schizophrenia (SCZ) and bipolar disorder (BD). All SNPs with a conjFDR value<0.05 (bidirectional association, i.e. association with SCZ given association with BD (condFDR<0.05) and association with BD given association with SCZ (condFDR<0.05)) are listed and sorted in each LD block. We defined the most significant SNP in each LD block based on the minimum conjFDR. All independent loci are listed consecutively, and the same locus number are used as in the condFDR<0.05 results (Table 1). Chromosome (Chr). Z-scores for each pleiotropic locus are provided, with minor allele (A1) and major allele (A2). All data were first corrected for genomic inflation. Model-based power analyses
Our model-free conditional FDR analyses circumvent the issue of bias due to model misspecification. However, to ascertain the impact of effective sample size and conditioning on relative power over using unconditioned FDR on current sample sizes, it is necessary to use a model-based approach that estimates the proportion and distribution of non-null SNPs [33]. We thus posit a mixture of null and non-null Gaussian distributions [34] (see Methods and Text S1). Resulting model fits are displayed in Figure 5 for schizophrenia and bipolar disorder for absolute z scores ≥3. Left panels are actual data, whereas right panels are hypothetical realizations from a doubling of effective sample size, generated from mixture model fits. Null densities largely coincide with the overall densities except for z scores with absolute value larger than 4, at which point the ratio of null to total SNPs, equal to the local false discovery rate (local FDR), is less than 0.5 (left panels of Figure 5). Thus, while highly polygenic, most non-null SNPs have local FDR much larger than 0.05. The local FDR does not drop below 0.05 until absolute z scores exceed 5. Far more of the “hidden” non-null SNPs lie below this significance threshold than above it. Many of these hidden SNPs lie just below the significance threshold, so that an effective doubling of the sample size produces a ∼30 times increase in number of rejected non-null SNPs with local FDR ≤0.05 (right panels of Figure 5).
Fig. 5. Histograms of absolute z-scores for bipolar disorder (BD, top panels) and schizophrenia (SCZ, bottom panels) for z-scores ≥3. 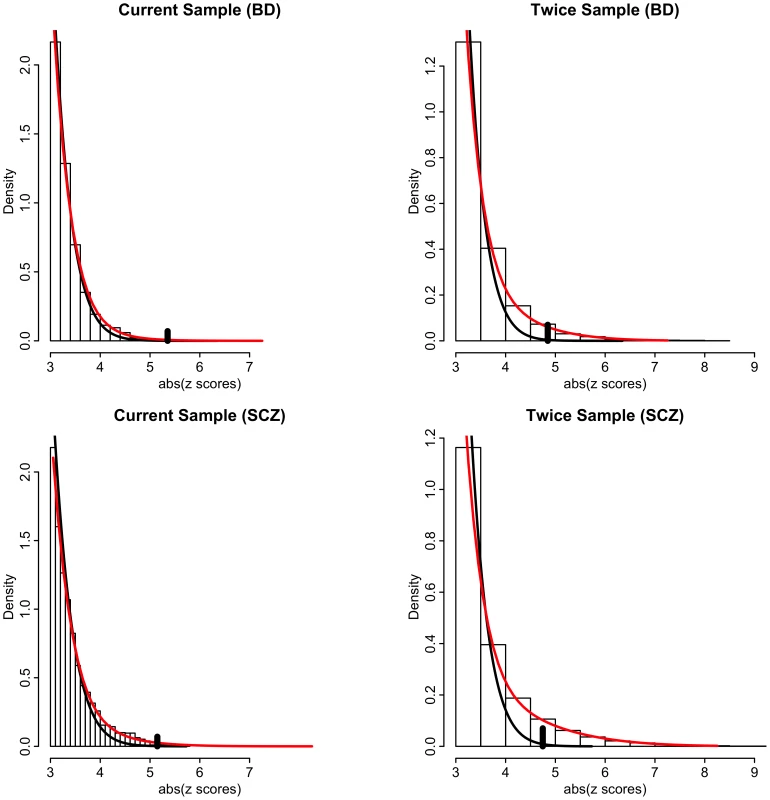
Left panels are actual data, whereas right panels are hypothetical realizations from a doubling of effective sample size, generated from mixture model fits of f(z) = π0f0(z)+(1−π0)f1(z) (see Text S1). Black lines are null sub-densities π0f0(z) and red lines are the full mixture densities f(z). The local false discovery rate is the ratio fdr = π0f0(z)/f(z). Vertical black bars in each plot indicate the cut-points where local fdr≤0.05. Another model-based analysis using a bivariate mixture of Gaussians showed that a very high proportion of the non-null schizophrenia SNPs are also non-null for bipolar disorder (and vice versa) leading to large increases in power when using the conditional FDR approach. This increase in power is also due to the large number of SNPs with p-values just below the Bonferroni threshold. Figure 6 shows the power, or sensitivity to detect non-null SNPs for differing local FDR cut points from unconditional and conditional local FDR and, for comparison, from a hypothetical doubling of the number of subjects. Using conditional over unconditional local FDR results in an increase of 15–20 times the number of non-null SNPs discovered for a local FDR≤0.05. The increase in power for conditional FDR, while dramatic, is not as large as what would be obtained by doubling the sample size. This is not unexpected, given that the highly polygenic non-null SNPs for schizophrenia and bipolar disorder, many just below the given significance thresholds, are largely but not completely overlapping. Note, given their highly polygenic distribution the vast majority of non-null SNPs remain undiscovered even using conditional FDR approaches or under an effective doubling of the number of subjects.
Fig. 6. ROC curves for bipolar disorder (top) and schizophrenia (bottom). 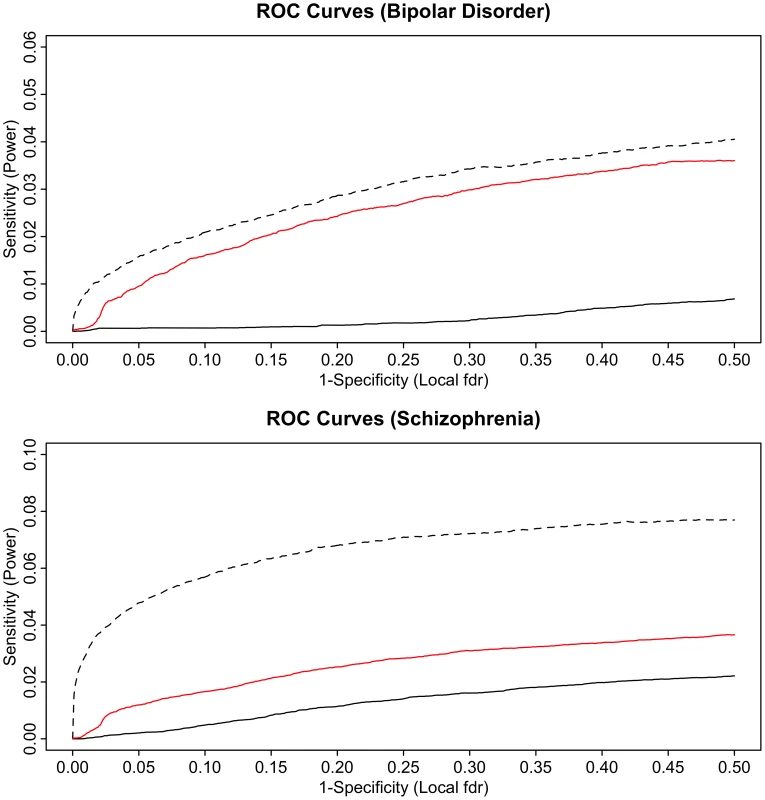
Solid black line show the proportion of non-null SNPs declared significant (sensitivity) for a given local false discovery rate (1-specificity). The corresponding ROC curves for bipolar disorder local FDR conditional on schizophrenia (top) and schizophrenia local FDR conditional on bipolar disorder (bottom) are given in red. Power resulting from a hypothetical doubling of effective subject sample size is given by the dashed black lines. To test for enrichment with a “control trait” with little or no polygenic overlap with psychiatric disease, we performed pleiotropy analysis using type 2 diabetes (T2D) GWAS data. The analyses confirmed that there was a very small level of pleiotropic enrichment between schizophrenia and T2D, leading to little if any improvement in statistical power (See Text S1 and Figure S7).
Discussion
In the present study we leveraged the power of GWAS data from two independent schizophrenia and bipolar disorder samples, and demonstrate how GWAS from associated psychiatric disorders can improve discovery of novel susceptibility loci. Using standard GWAS analytical methods, we identified only one significant locus. By applying traditional FDR methods in the separate GWAS samples, we found an additional 6 loci (2 in bipolar disorder, 4 in schizophrenia). Combining the independent schizophrenia and bipolar disorder GWAS samples, we identified a total of 58 loci in schizophrenia and 35 in bipolar disorders, with conditional FDR<0.05 as a threshold. Nine of the current loci have been identified earlier in larger samples using standard GWAS analytical methods (7 in schizophrenia, 5 in bipolar disorder, and 3 in combined samples), while 10 other loci have been reported to show borderline association with bipolar disorder or schizophrenia (Table S1). These results demonstrate the feasibility of using a cost-effective, pleiotropy-informed conditional FDR approach to discover common variants in schizophrenia and bipolar disorders.
The proposed statistical approach is based on the observation that all SNPs should not be treated as exchangeable. Rather, a SNP with large effects in two associated phenotypes has a higher probability of being a true non-null effect, and hence also a higher probability of being replicated in independent studies. We thus applied a conditional FDR approach we have previously developed for GWAS p-values [36], adapted from methods originally used for linkage analysis and microarray expression data [5], [37]. Decreased conditional FDR (equivalently, increased conditional TDR) for a given nominal p-value increases power to detect true non-null effects. Increased conditional TDR is directly related to increased replication effect sizes and replication rates in de novo samples. Using this conditional approach we were able to increase power to detect true non-null signals in independent studies for given nominal p-values cut-offs. Equivalently, in the conditional approach the FDR can be used to control FDR at a given level while increasing power to discover non-null SNPs over approaches that treat all SNPs as interchangeable. We also applied a previously developed conjunction FDR approach [36] to investigate which SNPs are pleiotropic, impacting risk of both schizophrenia and bipolar disorder. The conjunction statistic used is the maximum of the conditional FDR for schizophrenia given bipolar disorder and vice versa. SNPs that exceed a stringent conjunction threshold are thus highly likely to be non-null in the two phenotypes simultaneously.
The extra number of significant loci identified in the current study compared to ‘conventional’ GWAS methods is remarkable. The power analyses suggest that the large increase in power is due to the conditional FDR method, and not an implicit higher false discovery rate. Compared to conventional GWAS methods, traditional FDR methods only identified a few extra loci. The large increase in power came from using conditional FDR, which identified 14.5 times as many schizophrenia SNPs and 17.5 times as many bipolar SNPs (at FDR≤.05 level) compared to traditional FDR methods. This large increase in power seems to be due to two factors: the highly polygenic distribution of non-null SNPs and the high degree of pleiotropy between schizophrenia and bipolar disorder. We quantified this using a model-based mixture of null and non-null Gaussian distributions [34]. Mixture models estimate roughly 1.2% of tag SNPs are non-null in both bipolar disorder and schizophrenia. With over 1 million assayed SNPs in common between both phenotypes, the number of un-pruned, non-null SNPs is thus in excess of 12,000 in each phenotype. The vast majority of these non-null SNPs are hidden within the large proportion (∼99%) of null SNPs. Results are in line with recent findings of a high proportion of variation in schizophrenia susceptibility captured by common SNPs [6]. Taken together, these findings strongly suggest that Empirical Bayes methods, as outlined by Efron [27] should be the method of choice for analyzing GWAS of polygenic human phenotypes, and for leveraging pleiotropy with other complex humans traits.
The current findings of polygenic enrichment suggest that genetic pleiotropy is important in severe mental disorders, as has been indicated earlier [13]–[15], [24], [25]. However, by using conditional FDR, we were able to leverage the overlapping polygenetic architecture to identify more of the specific SNPs involved. The current approach identified 58 loci in schizophrenia compared to 7 in the original publication [13]. In bipolar disorder, the added power from schizophrenia GWAS identified 35 loci compared to two loci in the original study [14]. It is important to note that this improvement in gene discovery was obtained despite the much smaller number of controls in the current analyses because the original analyses of the two disorders used largely overlapping control samples. Since we used data from the 1000 Genomes Project (1KGP) to calculate LD structure, the number of loci can vary somewhat compared to the original analysis. For both disorders, most of the current findings were borderline significant in the original GWAS mega-analysis, or identified in other GWAS of partly overlapping samples, such as TRANK1 [38] and SYNE1 [32]. Several of the currently identified genes have been associated in previous candidate gene studies, such as DAOA [39].
Further, we identified 14 loci strongly associated with both disorders, compared to three in the original combined analysis [13], [14]. Previous studies have mainly used Fisher combined tests for joint analysis, which test the null-hypothesis of no association in any phenotype, which means that the signal can be driven by one of the phenotypes. In contrast, conjunction FDR analyses assess the evidence that either phenotype is non-null. It is therefore difficult to directly compare the current findings with previous results. However, of the three identified loci in previous combined analysis [13], [14], both the ITIH3-4 and CACNA1C regions were confirmed with the conjunctional analyses, but not the ANK3 region. We found the latter to be associated with bipolar disorder in the current analysis, which suggests that previous results found with Fisher combined statistics were driven by the stronger association in bipolar disorder [13], [14].
The current findings suggest some interesting gene candidates related to overlapping biology of bipolar disorder and schizophrenia. The Major Histocompatibility Complex loci associations with schizophrenia in previous studies [13], [17] seem not to be strengthened by the combined analysis with bipolar disorder, as they are minimally represented among the current pleiotropic loci (conjunction FDR analyses). The only pleiotropic gene on chromosome 6 was NOTCH 4, which has recently also been implicated in bipolar disorder [26], . The current findings strengthen the involvement of genes related to calcium homeostasis and receptor functioning. In schizophrenia, both CACNA1C and ANK3 were identified, and in bipolar disorder TRANK1 and CACNB2 were also significantly associated. CACNA1C and CACNB2 are related to key proteins involved in unifying the generation of calcium spikes in neocortical pyramidal neurons, which is a closely integrated process [41]. It is likely that such functional processes could be involved in generation of symptoms in severe mental disorders, and may thus be a potential therapeutic target. Interestingly, PPM1F, a Mg2+/Mn2+ dependent protein phosphatase, related to calcium/calmodulin-dependent protein kinase II gamma, was also associated with both disorders, and seems to further strengthen the hypothesis that alterations in electrophysiological function play a role in the pathophysiology of these disorders. It is also noteworthy that SNPs located close to MAD1L1 were significantly associated with both schizophrenia and bipolar disorder. MAD1L1 is located in a human accelerated region in the genome, which shows a large difference between humans and chimpanzees [42], and thus is suggested to be involved in human-specific traits.
In addition to uncovering more of the missing heritability of bipolar disorder and schizophrenia, the current findings support the notion that genetic pleiotropy is important for variation in human phenotypes [9], and suggest that there is substantial polygenic pleiotropy between bipolar disorder and schizophrenia which warrants further exploration. In the current study we defined pleiotropy as a single gene or variant being associated with more than one distinct phenotype (diseases) [9]. It is possible that some of the loci identified in the current study are not pleiotropic but rather underlie common aspects of the schizophrenia and bipolar disorder phenotypes [9]. This possibility warrants further investigation, but requires samples with more detailed information on clinical characteristics. In the current analyses we focused on SNPs, but gene-based pleiotropy is also of interest [10], as is the use of the current approach for developing methods for risk prediction across traits. However, these applications require raw data from individual participants and these data are not currently available.
In conclusion, the current findings demonstrate that in schizophrenia and bipolar disorder, pleiotropy-informed conditional FDR can improve the statistical power for detecting novel polygenic effects. Results from conditional and conjunction FDR analyses also offer insights into potential shared mechanistic relationships between these two mental disorders.
Materials and Methods
Ethics statement
The relevant institutional review boards or ethics committees approved the research protocol of the individual GWAS used in the current analysis and all human participants gave written informed consent.
Participant samples
We obtained complete GWAS results in the form of summary statistics p-values from the Psychiatric GWAS Consortium (PGC) – Schizophrenia and Bipolar Disorder Working Groups. The schizophrenia (SCZ) GWAS summary statistics results were obtained from the PGC Schizophrenia Work Group [13], which consisted of 9,394 cases with schizophrenia or schizoaffective disorder and 12,462 controls (52% screened) from a total of 17 samples from 11 countries. Semi-structured interviews were used by trained interviewers to collect clinical information, and operational criteria were used to establish diagnosis. The quality of phenotypic data was verified by a systematic review of data collection methods and procedures at each site, and only studies that fulfilled these criteria were included. Controls were selected from the same geographical and ethnic populations as cases. For further details on sample characteristics and quality control procedures applied, please see Ripke et al..
The bipolar disorder (BD) GWAS summary statistics results were obtained from the PGC Bipolar Disorder Working Group [14], which consisted of n = 16,731 participants, including 7481 cases and 9250 controls, from 11 studies from 7 countries. Standardized semi-structured interviews were used by trained interviewers to collect clinical information about lifetime history of psychiatric illness and operational criteria applied to make lifetime diagnosis according to recognized classifications. All cases have experienced pathologically relevant episodes of elevated mood (mania or hypomania) and meet operational criteria for a BD diagnosis. The sample consisted of BD I (84%), BD II (11%), schizoaffective disorder bipolar type (4%), and BD NOS (1%). Controls were selected from the same geographical and ethnic populations as cases. For further details on sample characteristics and quality control procedures applied, please see Sklar et al. [14].
Due to overlapping control samples in these studies, the common controls were split randomly, and divided between the two case-control analyses. All results presented here are based on these non-overlapping control samples, with n = 9379 cases and n = 7736 control samples in schizophrenia, and n = 6990 cases and n = 4820 controls in bipolar disorder analyses.
Statistical analyses
Analyses implemented here were motivated by previously published stratified FDR methods [5], [37]. However, we found that stratified empirical cdfs exhibited a high degree of variability. Instead, we computed empirical cdfs for the first phenotype conditional on nominal p-values of the second being at or below a given threshold. These conditional empirical cdfs vary more smoothly as a function of p-value thresholds in the second (associated) phenotype than do empirical cdfs employing disjoint strata. Conditional FDR estimates derived from the conditional empirical cdfs are a simple extension of Efron's Empirical Bayes FDR methods [33].
One advantage of the model-free empirical cdf approach is the avoidance of bias in conditional FDR estimates from model misspecification. However, there are inherent limitations to model-free approaches, especially with respect to inferring properties of the non-null distribution and, consequently, estimating power to detect non-null effects. We present complementary model-based analyses in the Supporting Information that estimate conditional and conjunctional local false discovery rate (fdr) [27]. Results presented in the Supporting Information using this model-based fdr corroborate the results of the model-free approaches presented here.
Genomic control
The empirical null distribution in GWAS is affected by global variance inflation due to population stratification and cryptic relatedness [43] and deflation due to over-correction of test statistics for polygenic traits by standard genomic control methods [34]. We applied a control method leveraging only intergenic SNPs which are likely depleted for true associations (Schork et al., under review). First, we annotated the SNPs to genic (5′UTR, exon, intron, 3′UTR) and intergenic regions using information from the 1KGP. As illustrated in Figure S1, there is an enrichment of functional genic regions in schizophrenia compared to the intergenic SNP category. We used intergenic SNPs because their relative depletion of associations suggests that they provide a robust estimate of true null effects and thus seem a better category for genomic control than all SNPs. We converted all p-values to z-scores and for each phenotype we estimated the genomic inflation factor λGC for intergenic SNPs. We computed the inflation factor, λGC as the median z-score squared divided by the expected median of a chi-square distribution with one degree of freedom and divided all test statistics by λGC. The conditional Q-Q plots for schizophrenia after control for genomic inflation are shown in Figure S1.
Conditional Q–Q plots for assessing pleiotropic enrichment
To assess pleiotropic enrichment, we used Q-Q plots conditioned on ‘pleiotropic’ effects. For a given associated phenotype, enrichment for pleiotropic signals is present if the degree of deflection from the expected null line is dependent on SNP associations with the second phenotype. We constructed conditional Q-Q plots of empirical quantiles of nominal −log10(p) values for SNP association with schizophrenia for all SNPs, and for subsets of SNPs determined by the nominal p-values of their association with bipolar disorder being at or below a given threshold. Specifically, we computed the empirical cumulative distribution of nominal p-values for a given phenotype for all SNPs and for SNPs with significance levels below the indicated cut-offs for the other phenotype (−log10(p)≥0, −log10(p)≥1, −log10(p)≥2, −log10(p)≥3 corresponding to p≤1, p≤0.1, p≤0.01, p≤0.001, respectively). The nominal p-values (−log10(p)) are plotted on the y-axis, and the empirical quantiles (−log10(q), where q = 1 - empirical cdf(p)) are plotted on the x-axis. To assess for polygenic effects below the standard GWAS significance threshold, we focused the conditional Q-Q plots on SNPs with nominal −log10(p)<7.3 (corresponding to p>5×10−8).
Conditional false discovery rate
Enrichment seen in the conditional Q-Q plots can be directly interpreted in terms of the FDR. Specifically, for a given p-value cutoff, the Bayes FDR [33], closely related to the q-value of Storey [44] is defined as
where π0 is the proportion of null SNPs, F0 is the null cdf, and F is the cdf of all SNPs, both null and non-null; see Text S1 for details on this simple mixture model formulation [33]. Under the null hypothesis, F0 is the cdf of the uniform distribution on the unit interval [0,1], so that Eq. [1] reduces to The cdf F can be estimated by the empirical cdf q = Νp/Ν, where Νp is the number of SNPs with p-values less than or equal to p, and N is the total number of SNPs. Replacing F by q and replacing π0 with unity in Eq. [2], we get which is biased upwards as an estimate of Eq. [2] [33]. If π0 is close to one, as is likely true for most GWAS, the increase in bias by setting it to unity in Eq. [3] is minimal. The quantity 1 – p/q, is therefore biased downward, and hence is a conservative estimate of the TDR = 1 - FDR. Note, Eq. [3] is the Empirical Bayes estimate of the Bayesian FDR described by Efron [33]. Referring to the formulation of the Q-Q plots, we see that Eq. [3] is equivalent to the nominal p-value divided by the empirical quantile, as defined earlier. Given the −log10 construction of the Q-Q plots we easily obtain demonstrating that the (conservatively) estimated FDR is directly related to the horizontal shift of the curves in the conditional Q-Q plots from the expected line x = y, with a larger shift corresponding to a smaller FDR. This is illustrated in Figure 1. For each p-value threshold in the associated trait (e.g. bipolar disorder), we calculated the conditional TDR as a function of p-value in the primary trait (e.g. schizophrenia, indicated by different colored curves) in Figure 1 according to Eq. [4].Conditional statistics—probability of association with one disorder
We define the conditional FDR as the posterior probability that a given SNP is null for the first phenotype given that the p-values for both phenotypes are as small or smaller as the observed p-values. Formally, this is given by
where p1 is the p-value for the first phenotype, p2 is the p-value for the second, and F(p1 | p2) is the conditional cdf and π0(p2) the conditional proportion of null SNPs for the first phenotype given that p-values for the second phenotype are p2 or smaller. Eq. [5] makes the assumption, reasonable for independent GWAS, that summary statistics are independent across phenotypes if they are null for at least one phenotype. We produce a conservative estimate of FDR(p1 | p2) by setting π0(p2) = 1 and using the empirical conditional cdf in place of F(p1 | p2) in Eq. [5]. This is a straightforward generalization of the Empirical Bayes approach developed by Efron [33]. We assign a conditional FDR value for schizophrenia given bipolar disorder p-values (denoted by FDR SCZ | BD) to each SNP by computing conditional FDR estimates on a grid and interpolating these estimates into a two-dimensional look-up table (Figure S2). All SNPs with conditional FDR<0.05 (−log10(FDR)>1.3) in schizophrenia given association with bipolar disorder are listed in Table 1 after ‘pruning’ (removing all SNPs with r2>0.2 based on 1KGP LD structure). We used the same procedure, in the opposite direction, to assign a conditional FDR value (denoted as FDR BD|SCZ) for bipolar disorder given schizophrenia p-values to each SNP. All SNPs with FDR<0.05 (−log10(FDR)>1.3) in bipolar disorder given schizophrenia are listed in Table 2 after pruning. A significance threshold of FDR<0.05 nominally corresponds to 5 false positives per 100 reported associations. We present a complementary model-based approach to estimating conditional FDR in the Text S1.Conjunction statistics—test of association with both phenotypes
In order to identify which of the SNPs were associated with schizophrenia and bipolar disorder we used a conjunction FDR procedure similar to that described for p-value statistics in Nichols et al. [45]. This minimizes the effect of a single phenotype driving the common association signal. Conjunction FDR is defined as the posterior probability that a given SNP is null for both phenotypes simultaneously when the p-values for both phenotypes are as small or smaller than the observed p-values. Formally, conjunction FDR is given by
where π0(p1, p2) is the proportion of SNPs null for both phenotypes simultaneously, F0(p1, p2) = p1 p2 is the joint null cdf, and F(p1, p2) is the joint overall cdf.Conditional empirical cdfs provide a model-free method to obtain conservative estimates of Eq. [6]. This can be seen as follows. Estimate the conjunction FDR by
where FDR SCZ | BD and FDR BD | SCZ (the estimated conditional FDRs described above) are conservative (upwardly biased) estimates of Eq. [5]. Thus, Eq. [7] is a conservative estimate of max{p1/F(p1 | p2), p2/F(p2 | p1)} = max{p1 F2(p2)/F(p1, p2), p2 F1(p1)/F(p1, p2)}. For enriched samples, p-values will tend to be smaller than predicted from the uniform distribution, so that F1(p1)≥p1 and F2(p2)≥p2. Hence, max{p1 F2(p2)/F(p1, p2), p2 F2(p1)/F(p1, p2)}≥max{p1 p2/F(p1, p2), p2 p1/F(p1, p2)} = p1 p2/F(p1, p2)≥π0(p1, p2) p1 p2/F(p1, p2). The last quantity is precisely the conjunction FDR defined by Eq. [6]. Thus, Eq. [7] is a conservative model-free estimate of the conjunction FDR. We present a complementary model-based approach to estimating conjunction FDR in the Text S1.We assigned the conjunction FDR values by interpolation into a bi-directional two-dimensional look-up table (Figure S3). All SNPs with conjunction FDR<0.05 (−log10(FDR)>1.3) with schizophrenia and bipolar disorder considered jointly are listed in Table 3 (after pruning), together with the corresponding z-scores and minor alleles. The z-scores were calculated from the p-values and the direction of effect was determined by the risk allele.
Conditional Manhattan plots
To illustrate the localization of the genetic markers associated with schizophrenia given their association with bipolar disorder, and vice versa, we used a ‘Conditional Manhattan plot’, plotting all SNPs within an LD block in relation to their chromosomal location. As illustrated in Figure 2 for schizophrenia, the large points represent the SNPs with conditional FDR<0.05, whereas the small points represent the non-significant SNPs. All SNPs without ‘pruning’ (removing all SNPs with r2>0.2 based on 1KGP LD structure) are shown. The strongest signal in each LD block is illustrated with a black line around the circles. This was identified by ranking all SNPs in increasing order, based on the conditional FDR value for schizophrenia given bipolar disorder, and then removing SNPs in LD r2>0.2 with any higher ranked SNP. Thus, the selected locus was the most significantly associated with schizophrenia in each LD block (Figure 2). A similar procedure was used in the conditional Manhattan plot for bipolar disorder given schizophrenia (Figure 3).
Conjunction Manhattan plots
To illustrate the localization of the pleiotropic genetic markers associated with both schizophrenia and bipolar disorder, we present a ‘Conjunction Manhattan plot’, plotting all SNPs with a significant conjunction FDR within an LD block in relation to their chromosomal location. As illustrated in Figure 4, the large points represent the significant SNPs (FDR<0.05), whereas the small points represent the non-significant SNPs. All SNPs without ‘pruning’ (removing all SNPs with r2>0.2 based on 1KGP LD structure) are shown, and the strongest signal in each LD block is illustrated with a black line around the circles. We ranked all SNPs based on the conjunction statistic and removed SNPs in LD r2>0.2 with any higher ranked SNP.
Model-based power analyses
While model-free approaches avoid assumptions that may bias results, it is necessary to take a model-based approach for assessing the power to detect non-null SNPs [33]. As in Eq. [1], let π0 be the proportion of null SNPs and let π1 = 1−π0 be the proportion of non-null SNPs. Following Yang et al. [34], the probability density f(zi) of the test statistic (z score) for the ith SNP is given by
where the null density f0(zi) corresponds to a N(0, σ02) distribution and the non-null density f1(zi) corresponds to a N(0, σ02+σ12) distribution. Both σ02 and σ12 are estimated from the data (see Text S1). The local false discovery rate, defined as the posterior probability that a SNP is non-null given the observed z score, is given by Efron and Tibshirani [35] Using this mixture of Gaussians formulation, we can assess relative power for gene discovery by determining the proportion of non-null SNPs with local fdr less than a given cut-off, e.g., 0.05. We can also determine the impact of scaling the effective sample size on the distribution f1(zi) of non-null SNPs.We extend this model to a bivariate framework by postulating a four groups model of bivariate Gaussians. Let zi be the bivariate z scores for the ith SNP for schizophrenia and bipolar disorder. The four groups mixture model is given by
where π0 is the proportion of SNPs which are null for both phenotypes, π1 and π2 are the proportion of SNPs which are non-null for schizophrenia and null for bipolar disorder (and vice versa), and π3 is the proportion of SNPs non-null for both simultaneously. The component densities f0, f1, f2, and f3 are bivariate Gaussian with zero mean and variance-covariance matrices estimated from the data. From model [9], we can compute conditional local fdr, similar to the conditional FDR described above. We can also determine the degree of pleiotropy from the estimated value of π3. Details of the methods for mixture models, local false discovery rate, and estimates of polygenicity, the degree of pleiotropic overlap, and power are presented in Text S1 and Figures S4, S5, S6, S7.Supporting Information
Zdroje
1. GlazierAM, NadeauJH, AitmanTJ (2002) Finding genes that underlie complex traits. Science 298 : 2345–2349.
2. HindorffLA, SethupathyP, JunkinsHA, RamosEM, MehtaJP, et al. (2009) Potential etiologic and functional implications of genome-wide association loci for human diseases and traits. Proc Natl Acad Sci U S A 106 : 9362–9367.
3. HirschhornJN, DalyMJ (2005) Genome-wide association studies for common diseases and complex traits. Nat Rev Genet 6 : 95–108.
4. YangJ, ManolioTA, PasqualeLR, BoerwinkleE, CaporasoN, et al. (2011) Genome partitioning of genetic variation for complex traits using common SNPs. Nat Genet 43 : 519–525.
5. YooYJ, PinnaduwageD, WaggottD, BullSB, SunL (2009) Genome-wide association analyses of North American Rheumatoid Arthritis Consortium and Framingham Heart Study data utilizing genome-wide linkage results. BMC Proc 3 Suppl 7: S103.
6. LeeSH, DeCandiaTR, RipkeS, YangJ, SullivanPF, et al. (2012) Estimating the proportion of variation in susceptibility to schizophrenia captured by common SNPs. Nat Genet 44 : 247–250.
7. StahlEA, WegmannD, TrynkaG, Gutierrez-AchuryJ, DoR, et al. (2012) Bayesian inference analyses of the polygenic architecture of rheumatoid arthritis. Nat Genet 44 : 483–489.
8. ManolioTA, CollinsFS, CoxNJ, GoldsteinDB, HindorffLA, et al. (2009) Finding the missing heritability of complex diseases. Nature 461 : 747–753.
9. SivakumaranS, AgakovF, TheodoratouE, PrendergastJG, ZgagaL, et al. (2011) Abundant pleiotropy in human complex diseases and traits. Am J Hum Genet 89 : 607–618.
10. WagnerGP, ZhangJ (2011) The pleiotropic structure of the genotype-phenotype map: the evolvability of complex organisms. Nat Rev Genet 12 : 204–213.
11. ChambersJC, ZhangW, SehmiJ, LiX, WassMN, et al. (2011) Genome-wide association study identifies loci influencing concentrations of liver enzymes in plasma. Nat Genet 43 : 1131–1138.
12. CotsapasC, VoightBF, RossinE, LageK, NealeBM, et al. (2011) Pervasive sharing of genetic effects in autoimmune disease. PLoS Genet 7: e1002254 doi:10.1371/journal.pgen.1002254.
13. RipkeS, SandersAR, KendlerKS, LevinsonDF, SklarP, et al. (2011) Genome-wide association study identifies five new schizophrenia loci. Nat Genet 43 : 969–976.
14. SklarP, RipkeS, ScottLJ, AndreassenOA, CichonS, et al. (2011) Large-scale genome-wide association analysis of bipolar disorder identifies a new susceptibility locus near ODZ4. Nat Genet 43 : 977–983.
15. LichtensteinP, YipBH, BjorkC, PawitanY, CannonTD, et al. (2009) Common genetic determinants of schizophrenia and bipolar disorder in Swedish families: a population-based study. Lancet 373 : 234–239.
16. PurcellSM, WrayNR, StoneJL, VisscherPM, O'DonovanMC, et al. (2009) Common polygenic variation contributes to risk of schizophrenia and bipolar disorder. Nature 460 : 748–752.
17. StefanssonH, OphoffRA, SteinbergS, AndreassenOA, CichonS, et al. (2009) Common variants conferring risk of schizophrenia. Nature 460 : 744–747.
18. CraddockN, OwenMJ (2007) Rethinking psychosis: the disadvantages of a dichotomous classification now outweigh the advantages. World Psychiatry 6 : 84–91.
19. VietaE, PhillipsML (2007) Deconstructing bipolar disorder: a critical review of its diagnostic validity and a proposal for DSM-V and ICD-11. Schizophr Bull 33 : 886–892.
20. FischerBA, CarpenterWTJr (2009) Will the Kraepelinian dichotomy survive DSM-V? Neuropsychopharmacology 34 : 2081–2087.
21. SimonsenC, SundetK, VaskinnA, BirkenaesAB, EnghJA, et al. (2011) Neurocognitive dysfunction in bipolar and schizophrenia spectrum disorders depends on history of psychosis rather than diagnostic group. Schizophr Bull 37 : 73–83.
22. CrowTJ (1986) The continuum of psychosis and its implication for the structure of the gene. Br J Psychiatry 149 : 419–429.
23. CraddockN, OwenMJ (2005) The beginning of the end for the Kraepelinian dichotomy. Br J Psychiatry 186 : 364–366.
24. CraddockN, O'DonovanMC, OwenMJ (2009) Psychosis genetics: modeling the relationship between schizophrenia, bipolar disorder, and mixed (or “schizoaffective”) psychoses. Schizophr Bull 35 : 482–490.
25. O'DonovanMC, CraddockN, NortonN, WilliamsH, PeirceT, et al. (2008) Identification of loci associated with schizophrenia by genome-wide association and follow-up. Nat Genet 40 : 1053–1055.
26. WilliamsHJ, CraddockN, RussoG, HamshereML, MoskvinaV, et al. (2011) Most genome-wide significant susceptibility loci for schizophrenia and bipolar disorder reported to date cross-traditional diagnostic boundaries. Hum Mol Genet 20 : 387–391.
27. Efron B (2010) Large-scale inference : empirical Bayes methods for estimation, testing, and prediction. Cambridge ; New York: Cambridge University Press. xii: , 263 p. p.
28. SchwederT, SpjotvollE (1982) Plots of P-Values to Evaluate Many Tests Simultaneously. Biometrika 69 : 493–502.
29. BenjaminiY, HochbergY (1995) Controlling the False Discovery Rate: A Practical and Powerful Approach to Multiple Testing. Journal of the Royal Statistical Society Series B (Methodological): Blackwell Publishing 289–300.
30. SteinbergS, de JongS, AndreassenOA, WergeT, BorglumAD, et al. (2011) Common variants at VRK2 and TCF4 conferring risk of schizophrenia. Hum Mol Genet 20 : 4076–4081.
31. FerreiraMA, O'DonovanMC, MengYA, JonesIR, RuderferDM, et al. (2008) Collaborative genome-wide association analysis supports a role for ANK3 and CACNA1C in bipolar disorder. Nat Genet 40 : 1056–1058.
32. GreenEK, GrozevaD, FortyL, Gordon-SmithK, RussellE, et al. (2012) Association at SYNE1 in both bipolar disorder and recurrent major depression. Mol Psychiatry doi: 10.1038/mp.2012.48.
33. EfronB (2007) Size, power and false discovery rates. The Annals of Statistics 35 : 1351–1377.
34. YangJ, WeedonMN, PurcellS, LettreG, EstradaK, et al. (2011) Genomic inflation factors under polygenic inheritance. Eur J Hum Genet 19 : 807–812.
35. EfronB, TibshiraniR (2002) Empirical bayes methods and false discovery rates for microarrays. Genet Epidemiol 23 : 70–86.
36. AndreassenOA, DjurovicS, ThompsonWK, SchorkAJ, KendlerKS, et al. (2013) Improved Detection of Common Variants Associated with Schizophrenia by Leveraging Pleiotropy with Cardiovascular-Disease Risk Factors. Am J Hum Genet 7;92 (2)
197–209 doi: 10.1016/j.ajhg.2013.01.001.
37. SunL, CraiuRV, PatersonAD, BullSB (2006) Stratified false discovery control for large-scale hypothesis testing with application to genome-wide association studies. Genet Epidemiol 30 : 519–530.
38. ChenDT, JiangX, AkulaN, ShugartYY, WendlandJR, et al. (2011) Genome-wide association study meta-analysis of European and Asian-ancestry samples identifies three novel loci associated with bipolar disorder. Mol Psychiatry
39. Detera-WadleighSD, McMahonFJ (2006) G72/G30 in schizophrenia and bipolar disorder: review and meta-analysis. Biol Psychiatry 60 : 106–114.
40. DiesetI, DjurovicS, TesliM, HopeS, MattingsdalM, et al. (2012) NOTCH4 Gene Expression is Upregulated in Bipolar Disorder. Am J Psychiatry in press
41. LarkumME, NevianT, SandlerM, PolskyA, SchillerJ (2009) Synaptic integration in tuft dendrites of layer 5 pyramidal neurons: a new unifying principle. Science 325 : 756–760.
42. PollardKS, SalamaSR, LambertN, LambotMA, CoppensS, et al. (2006) An RNA gene expressed during cortical development evolved rapidly in humans. Nature 443 : 167–172.
43. DevlinB, RoederK (1999) Genomic control for association studies. Biometrics 55 : 997–1004.
44. StoreyJD (2003) The positive false discovery rate: A Bayesian interpretation and the q-value. Annals of Statistics 2013–2035.
45. NicholsT, BrettM, AnderssonJ, WagerT, PolineJB (2005) Valid conjunction inference with the minimum statistic. Neuroimage 25 : 653–660.
Štítky
Genetika Reprodukčná medicína
Článek The G4 GenomeČlánek Mondo/ChREBP-Mlx-Regulated Transcriptional Network Is Essential for Dietary Sugar Tolerance inČlánek RpoS Plays a Central Role in the SOS Induction by Sub-Lethal Aminoglycoside Concentrations inČlánek Tissue Homeostasis in the Wing Disc of : Immediate Response to Massive Damage during DevelopmentČlánek Disruption of TTDA Results in Complete Nucleotide Excision Repair Deficiency and Embryonic LethalityČlánek DJ-1 Decreases Neural Sensitivity to Stress by Negatively Regulating Daxx-Like Protein through dFOXO
Článok vyšiel v časopisePLOS Genetics
Najčítanejšie tento týždeň
2013 Číslo 4- Gynekologové a odborníci na reprodukční medicínu se sejdou na prvním virtuálním summitu
- Je „freeze-all“ pro všechny? Odborníci na fertilitu diskutovali na virtuálním summitu
-
Všetky články tohto čísla
- Epigenetic Upregulation of lncRNAs at 13q14.3 in Leukemia Is Linked to the Downregulation of a Gene Cluster That Targets NF-kB
- A Big Catch for Germ Cell Tumour Research
- The Quest for the Identification of Genetic Variants in Unexplained Cardiac Arrest and Idiopathic Ventricular Fibrillation
- A Nonsynonymous Polymorphism in as a Risk Factor for Human Unexplained Cardiac Arrest with Documented Ventricular Fibrillation
- The Hourglass and the Early Conservation Models—Co-Existing Patterns of Developmental Constraints in Vertebrates
- Smaug/SAMD4A Restores Translational Activity of CUGBP1 and Suppresses CUG-Induced Myopathy
- Balancing Selection on a Regulatory Region Exhibiting Ancient Variation That Predates Human–Neandertal Divergence
- The G4 Genome
- Extensive Natural Epigenetic Variation at a Originated Gene
- Mouse Oocyte Methylomes at Base Resolution Reveal Genome-Wide Accumulation of Non-CpG Methylation and Role of DNA Methyltransferases
- The Environment Affects Epistatic Interactions to Alter the Topology of an Empirical Fitness Landscape
- TIP48/Reptin and H2A.Z Requirement for Initiating Chromatin Remodeling in Estrogen-Activated Transcription
- Aconitase Causes Iron Toxicity in Mutants
- Tbx2 Terminates Shh/Fgf Signaling in the Developing Mouse Limb Bud by Direct Repression of
- Mondo/ChREBP-Mlx-Regulated Transcriptional Network Is Essential for Dietary Sugar Tolerance in
- Sex-Differential Selection and the Evolution of X Inactivation Strategies
- Identification of a Tissue-Selective Heat Shock Response Regulatory Network
- Phosphorylation-Coupled Proteolysis of the Transcription Factor MYC2 Is Important for Jasmonate-Signaled Plant Immunity
- RpoS Plays a Central Role in the SOS Induction by Sub-Lethal Aminoglycoside Concentrations in
- Six Homeoproteins Directly Activate Expression in the Gene Regulatory Networks That Control Early Myogenesis
- Rtt109 Prevents Hyper-Amplification of Ribosomal RNA Genes through Histone Modification in Budding Yeast
- ATP-Dependent Chromatin Remodeling by Cockayne Syndrome Protein B and NAP1-Like Histone Chaperones Is Required for Efficient Transcription-Coupled DNA Repair
- Iron-Responsive miR-485-3p Regulates Cellular Iron Homeostasis by Targeting Ferroportin
- Mutations in Predispose Zebrafish and Humans to Seminomas
- Cytotoxic Chromosomal Targeting by CRISPR/Cas Systems Can Reshape Bacterial Genomes and Expel or Remodel Pathogenicity Islands
- Tissue Homeostasis in the Wing Disc of : Immediate Response to Massive Damage during Development
- All SNPs Are Not Created Equal: Genome-Wide Association Studies Reveal a Consistent Pattern of Enrichment among Functionally Annotated SNPs
- Functional 358Ala Allele Impairs Classical IL-6 Receptor Signaling and Influences Risk of Diverse Inflammatory Diseases
- The Tissue-Specific RNA Binding Protein T-STAR Controls Regional Splicing Patterns of Pre-mRNAs in the Brain
- Neutral Genomic Microevolution of a Recently Emerged Pathogen, Serovar Agona
- Genetic Requirements for Signaling from an Autoactive Plant NB-LRR Intracellular Innate Immune Receptor
- SNF5 Is an Essential Executor of Epigenetic Regulation during Differentiation
- Dialects of the DNA Uptake Sequence in
- Reference-Free Population Genomics from Next-Generation Transcriptome Data and the Vertebrate–Invertebrate Gap
- Senataxin Plays an Essential Role with DNA Damage Response Proteins in Meiotic Recombination and Gene Silencing
- High-Resolution Mapping of Spontaneous Mitotic Recombination Hotspots on the 1.1 Mb Arm of Yeast Chromosome IV
- Rod Monochromacy and the Coevolution of Cetacean Retinal Opsins
- Evolution after Introduction of a Novel Metabolic Pathway Consistently Leads to Restoration of Wild-Type Physiology
- Disruption of TTDA Results in Complete Nucleotide Excision Repair Deficiency and Embryonic Lethality
- Insulators Target Active Genes to Transcription Factories and Polycomb-Repressed Genes to Polycomb Bodies
- Signatures of Diversifying Selection in European Pig Breeds
- The Chromosomal Passenger Protein Birc5b Organizes Microfilaments and Germ Plasm in the Zebrafish Embryo
- The Histone Demethylase Jarid1b Ensures Faithful Mouse Development by Protecting Developmental Genes from Aberrant H3K4me3
- Regulates Synaptic Development and Endocytosis by Suppressing Filamentous Actin Assembly
- Sensory Neuron-Derived Eph Regulates Glomerular Arbors and Modulatory Function of a Central Serotonergic Neuron
- Analysis of Rare, Exonic Variation amongst Subjects with Autism Spectrum Disorders and Population Controls
- Scavenger Receptors Mediate the Role of SUMO and Ftz-f1 in Steroidogenesis
- DNA Double-Strand Breaks Coupled with PARP1 and HNRNPA2B1 Binding Sites Flank Coordinately Expressed Domains in Human Chromosomes
- High-Resolution Mapping of H1 Linker Histone Variants in Embryonic Stem Cells
- Comparative Genomics of and the Bacterial Species Concept
- Genetic and Biochemical Assays Reveal a Key Role for Replication Restart Proteins in Group II Intron Retrohoming
- Genome-Wide Association Studies Identify Two Novel Mutations Responsible for an Atypical Hyperprolificacy Phenotype in Sheep
- The Genetic Correlation between Height and IQ: Shared Genes or Assortative Mating?
- Comprehensive Assignment of Roles for Typhimurium Genes in Intestinal Colonization of Food-Producing Animals
- An Essential Role for Zygotic Expression in the Pre-Cellular Drosophila Embryo
- The Genome Organization of Reflects Its Lifestyle
- Coordinated Cell Type–Specific Epigenetic Remodeling in Prefrontal Cortex Begins before Birth and Continues into Early Adulthood
- Improved Detection of Common Variants Associated with Schizophrenia and Bipolar Disorder Using Pleiotropy-Informed Conditional False Discovery Rate
- Site-Specific Phosphorylation of the DNA Damage Response Mediator Rad9 by Cyclin-Dependent Kinases Regulates Activation of Checkpoint Kinase 1
- Npc1 Acting in Neurons and Glia Is Essential for the Formation and Maintenance of CNS Myelin
- Identification of , a Retrotransposon-Derived Imprinted Gene, as a Novel Driver of Hepatocarcinogenesis
- Aag DNA Glycosylase Promotes Alkylation-Induced Tissue Damage Mediated by Parp1
- DJ-1 Decreases Neural Sensitivity to Stress by Negatively Regulating Daxx-Like Protein through dFOXO
- Asynchronous Replication, Mono-Allelic Expression, and Long Range -Effects of
- Differential Association of the Conserved SUMO Ligase Zip3 with Meiotic Double-Strand Break Sites Reveals Regional Variations in the Outcome of Meiotic Recombination
- Focusing In on the Complex Genetics of Myopia
- Continent-Wide Decoupling of Y-Chromosomal Genetic Variation from Language and Geography in Native South Americans
- Breakpoint Analysis of Transcriptional and Genomic Profiles Uncovers Novel Gene Fusions Spanning Multiple Human Cancer Types
- Intrinsic Epigenetic Regulation of the D4Z4 Macrosatellite Repeat in a Transgenic Mouse Model for FSHD
- Bisphenol A Exposure Disrupts Genomic Imprinting in the Mouse
- Genetic and Genomic Architecture of the Evolution of Resistance to Antifungal Drug Combinations
- Transposable Elements Are Major Contributors to the Origin, Diversification, and Regulation of Vertebrate Long Noncoding RNAs
- Functional Dissection of the Condensin Subunit Cap-G Reveals Its Exclusive Association with Condensin I
- PLOS Genetics
- Archív čísel
- Aktuálne číslo
- Informácie o časopise
Najčítanejšie v tomto čísle- The G4 Genome
- Neutral Genomic Microevolution of a Recently Emerged Pathogen, Serovar Agona
- The Histone Demethylase Jarid1b Ensures Faithful Mouse Development by Protecting Developmental Genes from Aberrant H3K4me3
- The Tissue-Specific RNA Binding Protein T-STAR Controls Regional Splicing Patterns of Pre-mRNAs in the Brain
Prihlásenie#ADS_BOTTOM_SCRIPTS#Zabudnuté hesloZadajte e-mailovú adresu, s ktorou ste vytvárali účet. Budú Vám na ňu zasielané informácie k nastaveniu nového hesla.
- Časopisy













