Analýza dat v neurologii

XIV. Vyzkoušejte zvláštní typ neparametrického testování hypotéz: permutační testy – Fisherův exaktní test

V minulých dílech seriálu jsme uvedli „klasický“ postup testování statistických hypotéz, který stojí na výpočtu testové statistiky, u které známe její teoretické rozdělení pravděpodobnosti při platnosti nulové hypotézy. Toto tzv. parametrické testování vždy směřuje k práci s kvantily modelových rozdělení, která slouží jako teoretická referenční hodnota pro posuzování výsledku testu. Použitelnost modelových rozdělení je většinou podmíněna splněním určitých vstupních předpokladů. Pokud neznáme vhodná teoretická výběrová rozdělení, nebo naše data nesplňují vstupní předpoklady, existuje možnost tzv. neparametrického testování, které v typické podobě převádí kvantitativní hodnoty měřeného parametru na pořadí a dále pracuje již pouze s nimi. I u neparametrických testů jsme ale do určité míry limitováni velikostí vzorku a výběrovým rozdělením, i když v mnohem menší míře než u parametrické varianty.

Existuje však ještě jeden způsob testování, který v obecné rovině patří mezi neparametrické, ale s jiným principem než u ostatních testů. Tzv. permutační testy obracejí základní postup výpočtu a místo předpokládaného teoretického (referenčního) rozdělení pro testovou statistiku (např. t rozdělení u t‑testu) pracují jenom se získaným vzorkem. Kombinacemi naměřených hodnot je hodnocena pravděpodobnost, se kterou nastane právě pozorovaná varianta anebo varianty extrémnější, ještě více odchýlené od situace odpovídající platnosti nulové hypotézy. Jednoduše řečeno, přeskupováním naměřených dat hodnotíme, jak obvyklá/neobvyklá je právě získaná varianta. Jediným předpokladem zde je, že jednotlivé subjekty, na kterých provádíme měření, jsou vzájemně rovnocenné a zaměnitelné před začátkem vzorkování. V tomto díle seriálu vysvětlíme principy těchto testů na často využívaném Fisherově exaktním testu, v dalším díle se budeme permutačními testy zabývat obecněji.

Fisherův exaktní test, nazvaný po svém autorovi R. A. Fisherovi (Fisher, 1922), nám poslouží jako užitečná ukázka principů permutačního testování. Test se používá k hodnocení závislosti (asociace) dvou znaků nabývajících pouze dvou hodnot (ano/ne, 1/0; tzv. dichotomous variables). Běžným záznamem takových pozorování je 2 × 2 tabulka četností (příklad 1). Takové tabulky obecně označujeme jako kontingenční a k jejich zpracování se ještě v našem seriálu vrátíme. Nulovou hypotézou zde je nezávislost obou binárních znaků. Pokud nulovou hypotézu zamítneme, znamená to, že kombinace hodnot obou znaků nenastávají v sledované populaci náhodně a je mezi nimi závislost (asociace).

Fisherův exaktní test je postaven na velmi chytré, ale zároveň jednoduché myšlence. Místo spoléhání se na teoretickou testovací statistiku se známým teoretickým rozdělením, test nabízí přímý („exaktní“) výpočet pravděpodobnosti odchylky od nulové hypotézy. Výpočet nepracuje s žádným teoreticky předpokládaným referenčním rozdělením a v tomto smyslu nemá ani žádné předpoklady. Jednoduše simulačně generujeme varianty pozorované tabulky četností a určujeme pravděpodobnost výskytu všech obměn, které mají stejné součty řádků a sloupců (tzv. marginální četnosti) jako tabulka pozorovaná.

Klasifikační faktory jsou dvě nominální (binární) proměnné, u kterých sledujeme, zda u sledovaných subjektů nastaly nebo ne. Při výpočtu Fisherova exaktního testu se určuje pravděpodobnost nastání všech možných obměn četností A, B, C, D v tabulce, které dávají stejné marginální četnosti jako skutečně naměřená tabulka četností. Při platnosti nulové hypotézy, tedy nezávislosti obou faktorů, mají četnosti v buňkách tabulky tzv. hypergeometrické rozdělení. Toto rozdělení se využívá k výpočtu pravděpodobnosti výskytu pozorované tabulky a všech variant ještě extrémnějších, tedy více odchýlených od situace odpovídající platnosti nulové hypotézy.

Abychom dobře pochopili interpretační význam testu, musíme si uvědomit, že tabulka četností v příkladu 1 vzniká klasifikací subjektů (pacientů) současně dle dvou kritérií (např. pohlaví × obezita, dodržení dávkování léku × výskyt problémů). Každý hodnocený subjekt je klasifikován současně podle obou faktorů, které nabývají hodnoty ano/ne. Analýzou ověřujeme, zda spolu použité klasifikační míry souvisí, tedy například zda nedodržení dávkování léku vede k nižšímu počtu terapeutických odpovědí ve srovnání s pacienty, kde dávkování bylo dodrženo apod. Testování ověřuje, jak pravděpodobná je pozorovaná varianta a všechny ještě extrémnější varianty mezi všemi kombinacemi, které mohou teoreticky nastat při neměnných součtech řádků a sloupců tabulky.

Velkou výhodou testu je, že jej lze použít i v případě malých pozorovaných a očekávaných četností jednotlivých variant. Skutečně nenahraditelný je tento test u velmi málo četných jevů, kdy očekávaná četnost v ně­kte­rém z políček tabulky nepřesahuje hodnotu 10.

Fisherův exaktní test je svou robustností a přímočarostí výpočtu cenným nástrojem pro reálná klinická data. V klinické praxi totiž velmi často stojíme před úkolem srovnat skupiny pacientů, u kterých nastává nějaká událost nebo jev s nízkou četností a jsou ovlivňovány nějakým klasifikačním faktorem. Jako příklad uveďme:

• výskyt nežádoucích účinků po podání různých léků
• výskyt nějakého jevu ve skupinách pacientů dělených podle binárního kritéria
• společný výskyt (asociace) dvou různých typů nežádoucích účinků
• asociace binárního rizikového faktoru a výskytu nemoci (kouření vs karcinom plic)

Postup výpočtu Fisherova exaktního testu je ilustrativně popsán v příkladu 2 a obecně jej lze shrnout do následujících kroků, které jsou společné pro všechny permutační testy:

1. Pozorováním na N jedincích získáváme konkrétní naměřená data – tabulku četností.
2. Simulačně vytváříme další varianty, které kombinace obou znaků mohou teoreticky poskytnout, i když tyto v našem měření nenastaly. Pracujeme pouze s daným vzorkem a při zachování jeho velikosti a zachování tzv. marginálních četností generujeme další teoreticky možné varianty výsledku.
3. Hodnotíme, jak pravděpodobná je právě ta varianta, která nastala v našem měření, a dále všechny varianty extrémnější, které potvrzují neplatnost nulové hypotézy.

Příklad 2: příklad výpočtu Fisherova exaktního testu

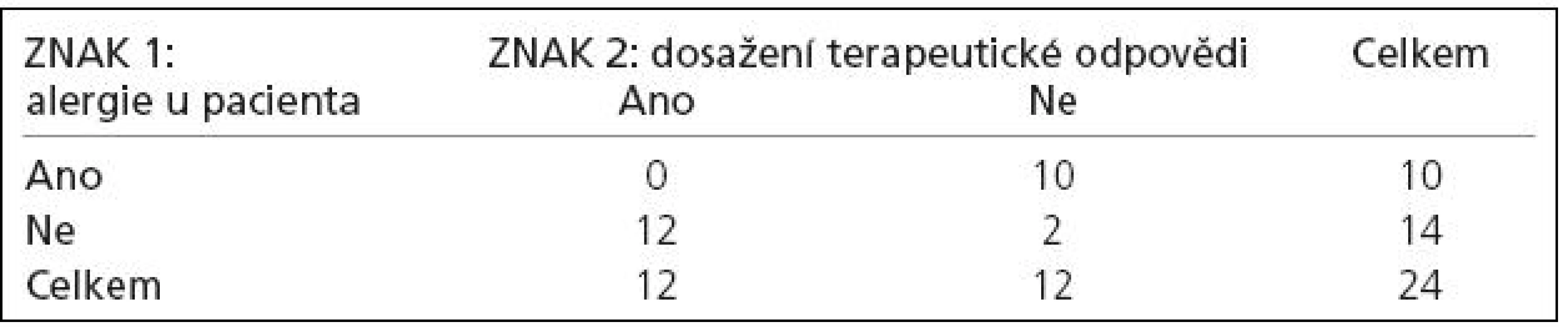
Testujeme, zda dosažení terapeutické odpovědi po určité léčbě souvisí s alergií u pacienta. Tedy přesněji, při daných četnostech alergiků (10) a dosažených odpovědí (12) testujeme nulovou hypotézu, že dosažení terapeutické odpovědi je stejně pravděpodobné u alergiků jako u ostatních pacientů. Víme‑li tedy, že 10 z 24 pacientů jsou alergici a že 12 z 24 pacientů dosáhlo terapeutické odpovědi, ptáme se, jaká je pravděpodobnost, že těchto 10 alergiků se vyskytuje rovnoměrně mezi pacienty s léčebnou odpovědí a bez ní (tab. 1).

K vlastnímu výpočtu směřujeme nejlépe touto otázkou: pokud jsme oněch 10 alergiků zachytili náhodně, jaká je pravděpodobnost, že právě jeden bude mezi pacienty s terapeutickou odpovědí a devět mezi pacienty bez odpovědi? Výpočet testu generuje všechny možné varianty 2 × 2 tabulky při fixních marginálních četnostech. Vyhodnotíme‑li a následně sečteme pravděpodobnost nastání pozorované tabulky a všech tabulek s extrémnějším výsledkem, dostaneme hladinu významnosti tzv. jednostranného testu. Pro hodnocení oboustranného testu musíme uvažovat stejně extrémní varianty tabulky ještě i v opačném směru. Příklad 2 představuje situaci, kdy při fixních součtech řádků a sloupců existuje pouze jedna varianta pozorované tabulky, která je pro distribuci léčebných odpovědí mezi alergiky extrémnější (tab. 2).

Pro každou variantu lze spočítat pravděpodobnost jejího nastání mezi všemi variantami zjištěné tabulky při fixních marginálních četnostech. Pro výpočet slouží následující vztah (symbol „!“ značí faktoriál počítaný z příslušných četností; označení četností A–D odpovídá značení v příkladu 1):

V našem příkladu tak získáváme pro zjištěnou tabulku a tabulku s ještě extrémnější odchylkou od nulové hypotézy následující pravděpodobnosti (někdy také označované jako P_cutoff):

• tabulka 1: P = 0,001346
• tabulka 2: P = 0,000034

Obě pravděpodobnosti jsou evidentně velmi malé, pokud je sečteme, získáváme p = 0,001379. Nastání pozorované tabulky četností a ještě extrémnější varianty je tedy velmi nepravděpodobné při platnosti nulové hypotézy.

Hladina významnosti Fisherova exaktního testu se získává součtem pravděpodobností určité množiny generovaných tabulek:

kde P je pravděpodobnost výskytu určité obměny četností a M je zmíněná množina tabulek:

• u jednostranného (one-tailed) testu:
• levostranného: sčítáme hodnoty P u všech tabulek, kde P je menší než nebo rovno pravděpodobnosti tabulky se zjištěnými četnostmi a kde četnost A (příklad 1) je menší než nebo rovna skutečně zjištěné četnosti
• pravostranného: sčítáme hodnoty P u všech tabulek, kde P je menší než nebo rovno pravděpodobnosti tabulky se zjištěnými četnostmi a kde četnost A (příklad 1) je větší než nebo rovna skutečně zjištěné četnosti
• u oboustranného (two‑tailed) testu: sčítáme hodnoty P u všech tabulek, kde P je menší než nebo rovno pravděpodobnosti tabulky se zjištěnými četnostmi

V našem příkladu tedy dostáváme p = 0,0014 pro případ jednostranného testu levostranného (alternativa k nulové hypotéze je negativní závislost obou faktorů) a p = 0,9999 pro případ jednostranného testu pravostranného (alternativa k nulové hypotéze je pozitivní závislost obou faktorů). Hladina významnosti pro oboustranný test je p = 0,0028.

Závěr příkladu 2

Zamítáme nulovou hypotézu nezávislosti obou faktorů. Na hladině významnosti p = 0,0014 potvrzujeme, že osoby s alergií významně častěji nedosahují léčebné odpovědi na danou léčbu (negativní závislost mezi výskytem alergie a dosažením léčebné odpovědi). Statistická významnost zde znamená, že je významný rozdíl v poměru počtu pacientů bez odpovědi/s odpovědí mezi alergiky a pacienty bez alergie.

Doufejme, že výpočet v příkladu 2 čtenáře neodradil. Generování všech možných variant tabulky četností by při větších vzorcích bylo velmi pracné, nikoli ale ve věku počítačů. Nabídku Fisherova exaktního testu nalezneme i v těch nejjednodušších statistických programech a s provedením výpočtu tedy není problém. Nadto existuje celá řada internetových stránek, které nabízejí rychlý výpočet jednostranného i oboustranného testu, stačí pouze zadat četnosti do tabulky. Jako příklad uvádíme následující odkaz: http://www.langsrud.com/fisher.htm.

Mnohem podstatnější než provedení výpočtu je ovšem samotná podstata testu, stále platná a univerzálně použitelná i po 80 letech od svého odvození. Bez předpokladů o referenčním rozdělení počítáme hladinu významnosti přímou kombinatorikou prováděnou na naměřených datech. Otázka, jak pravděpodobný je právě naměřený výsledek při platnosti nulové hypotézy, je jistě logicky přijatelná. Permutační testy nás tak osvobozují od svazujících předpokladů parametrických testů. Když k tomu u Fisherova exaktního testu ještě přidáme jasnou interpretaci výsledku a aplikovatelnost na malých vzorcích, není jistě důvod jej nepoužívat.

doc. RNDr. Ladislav Dušek, Dr.
Institut biostatistiky a analýz
Masarykova univerzita, Brno
e-mail: dusek@cba.muni.cz