-
Články
- Časopisy
- Kurzy
- Témy
- Kongresy
- Videa
- Podcasty
Analýza dat v neurologii X.
Vybrané otázky sumární statistiky
Autoři: L. Dušek; T. Pavlík; J. Koptíková
Působiště autorů: Masarykova univerzita, Brno ; Institut biostatistiky a analýz
Vyšlo v časopise: Cesk Slov Neurol N 2008; 71/104(4): 491-493
Kategorie: Okénko statistika
V minulém díle seriálu jsme dokončili výklad základních metod tzv. sumární statistiky, tedy statistických nástrojů popisujících výběrová rozdělení a pomáhajících formalizovat odhady jejich parametrů. V této části se s tímto tematickým okruhem rozloučíme diskuzním fórem, tedy odpovíme na otázky, které jsme dostali od čtenářů v mailech nebo na konferencích. Ze zkušenosti můžeme potvrdit, že všechny dotazy se týkají velmi častých problémů provázejících praktickou analýzu dat.
Otázka 1. Mohu použít současně aritmetický průměr a medián na stejných datech a ve stejném článku?
Ano, to je v zásadě možné. Pokud jde o data spojitá, je výpočet aritmetického průměru i mediánu bez problému možný a „numericky legitimní“. Jinými slovy oba ukazatele středu výběrového rozdělení existují a lze je odhadem vyčíslit. Jak jsme již probírali, lze jejich paralelní výpočet i doporučit jako kontrolu možné výrazné asymetrie výběrového rozdělení, odlehlých hodnot apod.
Pozor musíme dávat pouze na interpretaci obou odhadů. Medián je frekvenční střed a lze jej tedy označit za pořadovou střední hodnotu, zatímco průměr nebere pořadí hodnot v úvahu a je kvantitativním ukazatelem středu. Při popisu asymetrického výběrového rozdělení spojité náhodné veličiny, např. koncentrace látky v plazmě, tak může medián ukazovat na typickou naměřenou koncentraci (polovina všech měření je nižší) a průměr naopak na skutečně kvantitativní střed ve smyslu obsahu látky. Oba odhady jsou využitelné, ale mají jiný význam a budou oceněny, především pokud vycházejí číselně rozdílně. Naopak u symetrických rozdělení, kde jsou hodnoty mediánu a průměru přibližně stejné, nemá současné uvádění smysl.
Otázka 2. Narazil jsem na pojem „useknutý“ průměr. Co to znamená?
Tzv. useknuté odhady (trimmed estimates) jsou používány u velmi problematických rozdělení hodnot, kde hrozí vážné zkreslení odhadu (např. průměru) v důsledku několika málo extrémně odlehlých hodnot. Případné ovlivnění odhadu aritmetického průměru extrémními hodnotami lze eliminovat tím, že se záměrně vynechá například 10 % nejnižších a 10 % nejvyšších hodnot. Průměr je vypočten ze zbylých 80 % hodnot. Procento okrajových hodnot, které budou vynechány, se řídí podle situace a rozdělení dat, vždy ovšem musí být korektně uvedeno v metodice postupu. Pokud jsou useknuté odhady využity v jedné práci u více parametrů nebo u jedné veličiny měřené u více skupin jedinců, je jistě dobré, když se postupuje stejným způsobem a „useknutí“ je prováděno na stejné procentické hladině. Alternativou k těmto postupům je použití robustních statistických ukazatelů středové tendence, typicky mediánu, který není tak ovlivňován tvarem rozdělení jako průměr.
Otázka 3. Má smysl počítat interval spolehlivosti při velké velikosti vzorku, když vychází až nesmyslně „úzký“?
Vezměme si na pomoc intervalový odhad výběrového aritmetického průměru jako příklad:
IS : x– ± z1 – a/2 * (s/√n)
Již ze vzorce pro výpočet intervalu jasně vyplývá, že s velikostí vzorku n se interval spolehlivosti zužuje, neboť n je ve jmenovateli zlomku. Při velkých vzorcích může tedy být výsledný interval až nesmyslně úzký. Tím se ovšem nemění jeho interpretace. S pravděpodobností, která se rovná zvolené hladině spolehlivosti, interval pokrývá při opakovaném měření střední hodnoty parametru v cílové populaci, tedy hodnotu µ. Čistě teoreticky je velmi úzký interval vyjádřením vysoké přesnosti a spolehlivosti výsledku. Musíme si ovšem uvědomit, že takový interval informuje čtenáře pouze o výsledku a spolehlivosti odhadu aritmetického průměru, nikoli o rozdělení původních hodnot. Pokud se tazatel domnívá, že velmi úzký interval spolehlivosti je z tohoto hlediska zavádějící, doporučujeme interval spolehlivosti doplnit minimem a maximem původních hodnot nebo vhodně zvolenými percentily (např. 5–95%) původních hodnot.
Výše uvedená otázka vyplývá se situace, kdy se analytik dostane k retrospektivně nasbíranému a zbytečně velkému souboru dat. Máme-li možnost, měli bychom takovým situacím předcházet. V praxi totiž nemůžeme přistupovat k odhadům neplánovitě z finančních i z etických důvodů. Plánujeme takový počet opakovaných měření, který nám při daném rozptylu zajistí odhad průměru s požadovanou přesností a spolehlivostí. Plánování experimentů budeme věnovat celý blok seriálu, zde pouze uvádíme vztah, který umožní vypočítat velikost vzorku n nutnou k zajištění oboustranného intervalu spolehlivosti pro odhad průměru s požadovanou polovinou šířky označenou jako d, při hladině spolehlivosti 1 – a a směrodatné odchylce s. Jednoduchým vyjádřením z rovnice pro interval spolehlivosti získáváme:
n = [(z1 – a/2 * s)/d)]2
Otázka 4. Neustále se publikuje interval spolehlivosti pro průměr, existuje ale nějaký jednoduchý způsob, jak vyjádřit interval spolehlivosti pro medián?
Stejně jako v případě průměru je vhodné a možné doplnit intervalem spolehlivosti i medián. Metod pro výpočet je několik a lze je jednoduše rozdělit na parametrické a neparametrické. Jednoduchým příkladem parametrického výpočtu je použití binomického rozdělení pravděpodobnosti, které je obecně vhodné k výpočtu intervalu spolehlivosti pro jakýkoliv kvantil (označme jej q) [1]. Podstatou tohoto postupu je odhad intervalu spolehlivosti pro pravděpodobnost danou kvantilem q jako u binomické proměnné, přičemž výpočet nám nejprve definuje pořadí hodnot tvořících interval spolehlivosti pro medián v rámci naměřených hodnot. Jak již bylo uvedeno v předchozích částech seriálu, binomická proměnná má střední hodnotu rovnu n * q a rozptyl roven n * q *(1 – q). S pomocí těchto charakteristik jsme schopni spočítat hraniční hodnoty intervalu spolehlivosti pro pravděpodobnost q odpovídající pořadí, která určují hranice intervalu spolehlivosti (IS) pro medián, a to následovně: spodní hranicí 100(1 – a) % IS bude hodnota na pořadí j = n * q – z1 – a/2 * √(n * * q * (1 – q)), horní hranicí 100(1 – a) % IS pak bude hodnota na pořadí k = n * q + + z1 – a/2 * √(n * q *(1 – q)), kde z1 – a/2 je příslušný kvantil normálního rozdělení (pro oboustranný 95% IS je z(0,975) == 1,96). Jednoduše řečeno si tedy pomocí těchto vztahů spočítáme pořadí hodnot, které tvoří hranice intervalu spolehlivosti a tyto hodnoty potom podle pořadí dohledáme v naměřeném souboru dat.
Zde je nutné poznamenat, že na rozdíl od intervalu spolehlivosti pro aritmetický průměr nemusí být interval spolehlivosti pro medián symetrický. Příklad výpočtu intervalu spolehlivosti pro medián s pomocí binomického rozdělení je uveden na schématu 1.
Schéma 1. Výpočet intervalu spolehlivosti pro medián s použitím aproximace na binomické rozložení. 
Z neparametrických metod výpočtu intervalu spolehlivosti pro medián je nutné se zmínit o metodě založené na tzv. bootstrap algoritmu [2]. Jedná se o odhad rozložení hodnot mediánu opakovaným vzorkováním pozorovaných dat. Opakovaně, např. 200krát, vybíráme s opakováním z pozorovaných hodnot soubor o stejném n (tzv. bootstrap vzorek), z něhož následně spočítáme medián. Takto dostaneme pro každý bootstrap vzorek jednu hodnotu mediánu, které pak dohromady popisují množinu hodnot, jichž může medián nabývat (rozdělení pravděpodobnosti pro odhad mediánu). Interval spolehlivosti pro medián ve zdrojových datech pak stanovíme na základě příslušných kvantilů souboru mediánů získaných pomocí opakovaného vzorkování původních hodnot, tedy v případě 95% intervalu spolehlivosti jej budou definovat 2,5% kvantil a 97,5% kvantil. Výhodou této neparametrické metody je její nezávislost na jakýchkoliv statistických předpokladech, kterými jsou někdy omezeny parametrické metody. Na druhou stranu, pro získání relevantního odhadu je nutné dostatečné množství opakovaných výběrů, což nemusí být vždy snadné při malé velikosti původního souboru. Více informací může čtenář nalézt v učebnici Efron a Tibshirani [2].
Otázka 5. V jednom díle statistického seriálu jste se věnovali transformacím dat, spadá do této kapitoly i tzv. standardizace normálního rozdělení?
Standardizace normálního rozdělení není transformací v pravém slova smyslu, jde spíše o číselné sjednocení opakovaně měřených výběrových normálních rozdělení. Měříme-li například výšku postavy ve třech různých populacích, vždy dostaneme jiné výběrové rozdělení rozsahu hodnot a tedy také jiný aritmetický průměr. Ve všech případech budou ale pozorované hodnoty vykazovat stejný modelový typ rozdělení, a to rozdělení normální. Standardizace náhodné veličiny X (reálně naměřené hodnoty) převádí její výběrové normální rozdělení na tzv. standardizované (normované) normální rozdělení s označením náhodné veličiny Z (mezinárodně používáno). Původní výběrová rozdělení mají svůj aritmetický průměr a rozptyl, standardizované normální rozdělení je ale jen jedno a má průměr roven 0 a rozptyl roven 1 : Z ∼ N (0; 1). Význam standardizace spočívá v tom, že distribuční funkce standardizovaného normálního rozdělení je tabelována a my tak snadno zjistíme číselné hodnoty kvantilů rozdělení. Kvantily označené zq jsme ostatně používali i při výpočtech intervalů spolehlivosti pro průměr, takže jejich užití již čtenáři zaznamenali i v tomto seriálu.
V praxi standardizaci provádíme jednoduše tak, že od každé naměřené hodnoty náhodné veličiny Xi odečteme průměr x– (výběrový odhad nebo teoretickou hodnotu) a rozdíl vydělíme směrodatnou odchylkou s (výběrovým odhadem nebo teoretickou hodnotou). Ke každé hodnotě Xi tak získáváme komplementárně hodnotu Zi postupem znázorněným na obr. 1. Praktické využití standardizace normálního rozdělení lze stručně popsat takto:
Obr. 1. Schéma znázorňující standardizaci výběrového normálního rozdělení náhodné veličiny X. 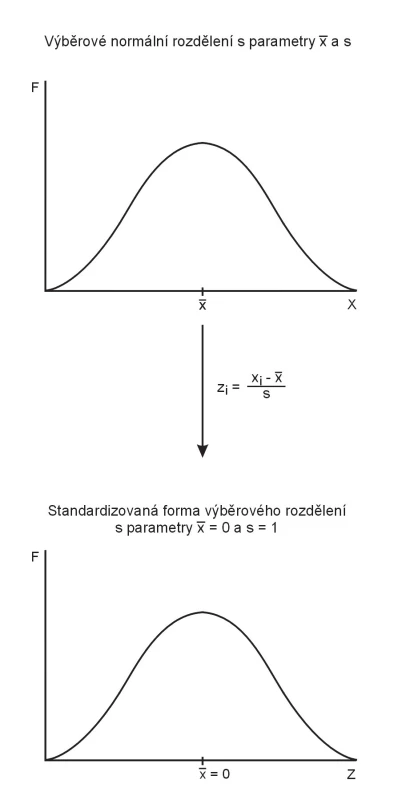
- Můžeme přímo pracovat s hodnotami Z a srovnávat čísla získaná standardizací naměřených dat (obr. 1) proti publikovaným normám, které byly zjištěny na rozsáhlé populaci a slouží jako reference. Tímto způsobem jsou často porovnávány výsledky měření veličiny X na konkrétní populaci s celoevropskými nebo světovými normami. To je zvláště potřebné za situace, kdy se rozdělení znaku X mění s věkem nebo je různé pro různá pohlaví. V tomto případě naměříme konkrétní hodnotu xi u konkrétního jedince a tuto hodnotu standardizujeme na hodnotu zi s využitím průměru a směrodatné odchylky zjištěné na referenční populaci (teoreticky dostupné nebo tabelované hodnoty). Jelikož zde nepoužíváme výběrové odhady průměru a směrodatné odchylky, ale referenční hodnoty, píšeme potom vztah pro standardizaci na rozdíl od příkladu na obr. 1 obecněji: Z = (X – µ) / s. Víme‑li například, že norma pro hodnoty X odpovídající pohlaví a věku daného jedince je Z ≤ 2, pak získanou hodnotu zi takto poměřujeme se standardizovanou normou již v hodnotách Z. Někdy se porovnávané standardizované hodnoty označují jako „Z skóre“.
- Můžeme lehce s použitím tabulek nebo počítače pracovat s kvantily rozdělení z a zjistit tak kvantilovou pozici jakékoli hodnoty náhodné veličiny X. V tomto případě nejprve nalezneme příslušný kvantil zq, který odpovídá hledané kvantilové pravděpodobnosti q (např. z0,975 = 1,96). Následně provedeme v podstatě zpětný výpočet standardizace a zjistíme hodnotu veličiny X, která je hledaným kvantilem q v naměřeném výběrovém rozdělení hodnot: xq = zq * s + µ.
doc. RNDr. Ladislav Dušek, Dr.
Institut biostatistiky a analýz
Masarykova univerzita, Brno
e-mail: dusek@cba.muni.cz
Zdroje
1. Conover WJ. Practical Nonparametric Statistics. 2nd ed. New York: John Wiley & Sons 1980.
2. Efron B, Tibshirani RJ. An introduction to the bootstrap. New York: Chapman and Hall 1993.
Štítky
Detská neurológia Neurochirurgia Neurológia
Článok vyšiel v časopiseČeská a slovenská neurologie a neurochirurgie
Najčítanejšie tento týždeň
2008 Číslo 4- Metamizol jako analgetikum první volby: kdy, pro koho, jak a proč?
- Kombinace metamizol/paracetamol v léčbě pooperační bolesti u zákroků v rámci jednodenní chirurgie
- Antidepresivní efekt kombinovaného analgetika tramadolu s paracetamolem
- Neuromultivit v terapii neuropatií, neuritid a neuralgií u dospělých pacientů
- Srovnání analgetické účinnosti metamizolu s ibuprofenem po extrakci třetí stoličky
-
Všetky články tohto čísla
- Stenóza vnitřní krkavice – endarterektomie nebo stent?
- Srovnání karotické endarterektomie a stentingu – výsledky jednoho pracoviště
- Patofyziologie kompresivní radikulopatie
- Timing karotické endarterektomie
- Přínos statické počítačové posturografie ke skríningovému vyšetření kvantifikace posturální rovnováhy
- Botulotoxin v léčbě detruzorové hyperaktivity u pacientek s roztroušenou sklerózou
- Výskyt epileptických záchvatů a/ nebo epileptiformní EEG abnormity u dětí s dětským a atypickým a utizmem
- Komentář ke článku Schreiberová et al. Sedace kombinací dexmedetomidin- ketamin- midazolam pro endovaskulární léčbu mozkových arteri ovenózních malformací a stenóz karotických tepen
- Sedace kombinací dexmedetomidin-ketamin- midazolam pro endovaskulární léčbu mozkových arteri ovenózních malformací a stenóz karotických tepen
- Vývoj adaptace rovnovážného systému po operacích vestibulárního schwannomu
- Komplikace léčby těžké spasticity implantabilními pumpovými systémy
- Analýza souboru pacientů s kraniocerebrálním poraněním léčených na Pracovišti dětské medicíny FN Brno v období let 2000–2007
- Výsledky operační léčby ne uromuskulárních deformit páteře
- Tuberózní skleróza: optimalizace postupu její DNA di agnostiky
- Cerebelární mutizmus po resekci meduloblastomu u dítěte – kazuistika
- Léky navozený systémový lupus erythematodes při terapii interferonem beta‑1b – kazuistika
- Webové okénko
-
Analýza dat v neurologii X.
Vybrané otázky sumární statistiky - Doporučené postupy pro di agnostiku Alzheimerovy nemoci a dalších onemocnění spojených s demencí
- Kraniocerebrální poranění v dětském věku
- Česká a slovenská neurologie a neurochirurgie
- Archív čísel
- Aktuálne číslo
- Informácie o časopise
Najčítanejšie v tomto čísle- Stenóza vnitřní krkavice – endarterektomie nebo stent?
- Výskyt epileptických záchvatů a/ nebo epileptiformní EEG abnormity u dětí s dětským a atypickým a utizmem
- Léky navozený systémový lupus erythematodes při terapii interferonem beta‑1b – kazuistika
- Timing karotické endarterektomie
Prihlásenie#ADS_BOTTOM_SCRIPTS#Zabudnuté hesloZadajte e-mailovú adresu, s ktorou ste vytvárali účet. Budú Vám na ňu zasielané informácie k nastaveniu nového hesla.
- Časopisy



