-
Články
- Časopisy
- Kurzy
- Témy
- Kongresy
- Videa
- Podcasty
Pharmacodynamics, Population Dynamics, and the Evolution of Persistence in
When growing populations of bacteria are confronted with bactericidal antibiotics, the vast majority of cells are killed, but subpopulations of genetically susceptible but phenotypically resistant bacteria survive. In accord with the prevailing view, these “persisters” are non - or slowly dividing cells randomly generated from the dominant population. Antibiotics enrich populations for pre-existing persisters but play no role in their generation. The results of recent studies with Escherichia coli suggest that at least one antibiotic, ciprofloxacin, can contribute to the generation of persisters. To more generally elucidate the role of antibiotics in the generation of and selection for persisters and the nature of persistence in general, we use mathematical models and experiments with Staphylococcus aureus (Newman) and the antibiotics ciprofloxacin, gentamicin, vancomycin, and oxacillin. Our results indicate that the level of persistence varies among these drugs and their concentrations, and there is considerable variation in this level among independent cultures and mixtures of independent cultures. A model that assumes that the rate of production of persisters is low and persisters grow slowly in the presence of antibiotics can account for these observations. As predicted by this model, pre-treatment with sub-MIC concentrations of antibiotics substantially increases the level of persistence to drugs other than those with which the population is pre-treated. Collectively, the results of this jointly theoretical and experimental study along with other observations support the hypothesis that persistence is the product of many different kinds of errors in cell replication that result in transient periods of non-replication and/or slowed metabolism by individual cells in growing populations. This Persistence as Stuff Happens (PaSH) hypothesis can account for the ubiquity of this phenomenon. Like mutation, persistence is inevitable rather than an evolved character. What evolved and have been identified are genes and processes that affect the frequency of persisters.
Published in the journal: Pharmacodynamics, Population Dynamics, and the Evolution of Persistence in. PLoS Genet 9(1): e32767. doi:10.1371/journal.pgen.1003123
Category: Research Article
doi: https://doi.org/10.1371/journal.pgen.1003123Summary
When growing populations of bacteria are confronted with bactericidal antibiotics, the vast majority of cells are killed, but subpopulations of genetically susceptible but phenotypically resistant bacteria survive. In accord with the prevailing view, these “persisters” are non - or slowly dividing cells randomly generated from the dominant population. Antibiotics enrich populations for pre-existing persisters but play no role in their generation. The results of recent studies with Escherichia coli suggest that at least one antibiotic, ciprofloxacin, can contribute to the generation of persisters. To more generally elucidate the role of antibiotics in the generation of and selection for persisters and the nature of persistence in general, we use mathematical models and experiments with Staphylococcus aureus (Newman) and the antibiotics ciprofloxacin, gentamicin, vancomycin, and oxacillin. Our results indicate that the level of persistence varies among these drugs and their concentrations, and there is considerable variation in this level among independent cultures and mixtures of independent cultures. A model that assumes that the rate of production of persisters is low and persisters grow slowly in the presence of antibiotics can account for these observations. As predicted by this model, pre-treatment with sub-MIC concentrations of antibiotics substantially increases the level of persistence to drugs other than those with which the population is pre-treated. Collectively, the results of this jointly theoretical and experimental study along with other observations support the hypothesis that persistence is the product of many different kinds of errors in cell replication that result in transient periods of non-replication and/or slowed metabolism by individual cells in growing populations. This Persistence as Stuff Happens (PaSH) hypothesis can account for the ubiquity of this phenomenon. Like mutation, persistence is inevitable rather than an evolved character. What evolved and have been identified are genes and processes that affect the frequency of persisters.
Introduction
While it is convenient to consider genetically identical populations of bacteria as collections of physiologically homogeneous cells, they are commonly composed of phenotypically different subpopulations. Usually by some form of stochastic switch, during the course of growth or at stationary phase, bacteria of one phenotype produce cells of different phenotypes [1]–[6]. From the practical perspective of antibiotic treatment, the most important of these phenotypically distinct subpopulations are the persistent cells. As first reported by John Bigger [7], when growing populations of bacteria are confronted with bactericidal antibiotics, the majority of cells are killed but a minority survive. Upon re-culture, these surviving bacteria are as sensitive to antibiotics as the cells from whence they were derived. And, when exposed to bactericidal antibiotics, they too produced minority populations of survivors. Bigger called these phenotypically resistant but genetically susceptible subpopulations of bacteria “persisters”.
In his original 1944 studies, Bigger used Staphylococcus pyogenes (now Staphylococcus aureus) and the beta-lactam antibiotic penicillin. Since then, persistence has been demonstrated for a number of different species of bacteria with many classes of antibiotics [8]–[15]. Indeed, persistence has been suggested to be a universal character, not only among the bacteria [16] but also fungi [17], [18], the cells responsible for neoplasms [19] and doubtless other somatic cells. Although it is not absolutely clear how important persister subpopulations are to the course of antibiotic treatment in human patients, at least in theory persisters can prolong the course therapy, prevent clearance and promote the generation and ascent of bacteria with heritable resistance [20], [21]. There is in fact recent clinical evidence for persistence retarding the rate of, and possibly preventing the clearance of bacterial infections in antibiotic treated humans [22], [23].
What are persisters? In accord with the prevailing view, bacterial persisters are subpopulations of cells that are refractory to antibiotics because they are either not dividing or they are dividing at very low rates [16], [24], [25], [26]. In this perspective, one class of persisters are generated at random by a stochastic switch from non-persisters during exponential growth, remain in that state for some time and then revert to the non-persister state [24], [25]. It has been proposed that persisters are also generated at stationary phase as, upon transfer to fresh medium, they take longer to come out of lag (“wake up”) than non-persisters [27]. Further work has shown that during the first 1.5 hours following inoculation into fresh media, the class of non-growing persister cells generated during stationary phase are not yet completely dormant and not yet refractory to antibiotic treatment but rather complete this transition during this time period [28]. Thus, by killing the majority population of replicating cells, antibiotics increase the relative frequency of these phenotypically resistant but genetically susceptible bacteria, i.e. antibiotics reveal the existence of persister subpopulations, but have no role in their generation. A recent report by Dörr and colleagues questions the generality of this perspective on the role of antibiotics in the generation of persisters [29]. In their study with E coli, pre-exposure to the fluoroquinolone ciprofloxacin increased fraction of cells surviving exposure to bactericidal concentrations of this drug (also see [30]).
In this investigation, we use mathematical models, computer simulations and experiments with Staphylococcus aureus and antibiotics of four classes to determine the effects of different antibiotics and their concentrations on the level of persistence and more broadly elucidate the contribution of these drugs to the formation of persisters. We interpret the results of these experiments to be inconsistent with the hypothesis that persisters are a unique, or even very few types of subpopulations that are generated at random, and that bactericidal antibiotics only reveal their existence by killing growing cells. Our results provide evidence that the singular observation that pre-exposure of E. coli to ciprofloxacin increases the frequency of persisters in generally applicable. We show that it not only obtains with a very different species of bacteria, but also with antibiotics of different classes. Based on these theoretical and experimental results, the results of other studies of persistence, and evolutionary considerations we postulate that persisters are: (i) the product of many different of errors and/or processes that result in transient periods of inhibition of the cell replication cycle of individual metabolizing bacteria and/or affect the amount of time required for the transition from stationary phase to replication (the lag), and (ii) the rates at which these processes occur are influenced by environmental stresses including the presence of antibiotics. We propose that persistence is analogous to mutation, an inevitable rather than an evolved character.
Results
Theoretical considerations
We open this report with a quantitative straw person. We use a simple mathematical model of to illustrate what would be anticipated in our experiments if persisters are generated at random at a rate that is independent of the nature and quantity of antibiotics that select for these phenotypically resistant cells, the null hypothesis. In this model, there are three populations of bacteria, one that is replicating at a high rate and two that are not replicating, persisters, with densities and designations, N, PE and PS, respectively. As shown by Balaban and colleagues [24], we assume that these persisters are of two types: 1 - those that are produced at stationary phase, PS, and those that are produced when the cells are growing exponentially, PE. These persister cells are generated from the N population at maximum rates, fs and fe, per cell per hour and return to the N state at maximum rates gs and ge, per cell per hour. To distinguish between growing and stationary phase, we assume a logistic function (1-NT/K) where NT is the total density of bacteria and K the saturation (stationary phase) density, where NT≤K. The rate of growth of the bacteria, the rate of production of persisters from growing cells N→PE, and the rate of return from the persister to the growing state, PS→N and PE→N is proportional to (1-NT/K). The idea being that these rates are greater when the population is further from stationary phase and these processes cease when the population is at stationary phase, NT = K. The rate of production of stationary phase persisters, N→PS, on the other hand is proportional to NT/K and thereby increases as the population approaches stationary phase and continues during stationary phase.
For the pharmacodynamics of the antibiotic, and the N population we use a Hill function [31],
where A is the concentration of the antibiotic, VMAX the maximum growth rate of the bacteria, VMIN the minimum growth rate, (VMIN≤0), the minimum inhibitory concentration (MIC) of the antibiotic and k the hill coefficient, a shape parameter. With these definitions and assumptions, the rates of change in the densities of these three states of bacteria are given by where NT = N+PE+PSTo illustrate the properties of this model, we use a finite step size Euler method to numerically solve these differential equations. For these computer simulations, the generation and loss of persisters are stochastic processes, which we simulate by a Monte Carlo process. For example, when the rectangularly distributed random number, r (0≤r≤1) is less than the product of the fe(1-NT/K) *N*Δt, a single individual of the PE persister population is generated and a single individual of the N population is lost. The step sizes of these simulations, ΔT, are chosen so that during any finite step, the probability of generating a persister is less than 1. These computer simulations were programmed in Berkeley Madonna. Copies of this program and instructions for its used are available at www.eclf.net.
Predictions
In Figure 1A, we present the Hill function antibiotic concentration – dependent growth/death rates for bacteria confronting bactericidal drugs with different combinations of MICs, VMINs and κs. In Figure 1B, we follow the dynamics of change in density of normal, N, bacteria and bacteria of the stationary and exponential phase persister states, PE and PS, respectively. Initially, the population in this simulation consisted solely of 103 N cells per ml. Within short order, the N population reaches the saturation level K. During the course of its ascent, persisters of the PS and PE populations also accumulate. Although the density of the persisters generated during exponential growth, PE, stopped increasing when the N population at large NT, enters stationary phase, NT = K, the stationary phase persister population PS, continued to ascend.
Fig. 1. Pharmacodynamics and anticipated population dynamics of treatment. 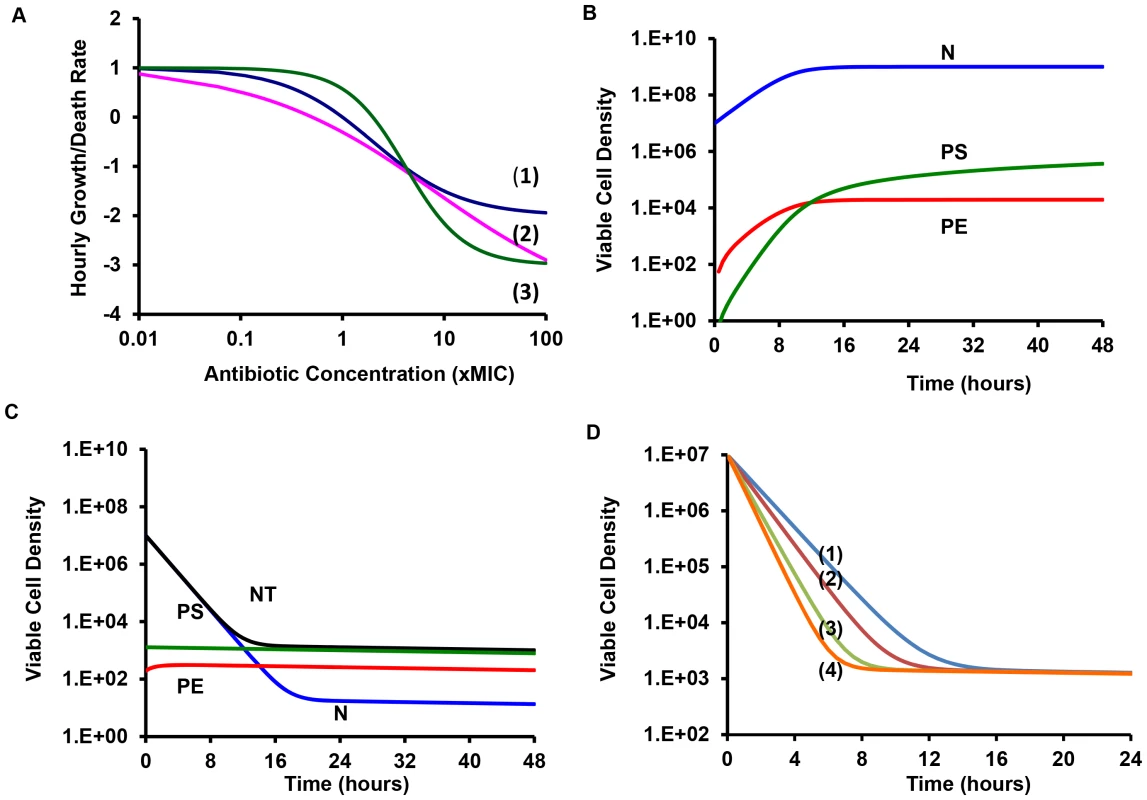
(A) Antibiotic-dependent growth/death rates. Hill function VMAX = 1 for all, the values of VMIN, MIC, κ are respectively (1) −1: 1: 1, (2) −3, 1, 1, (3) −5.0, 0.5, 0.5. (B) Changes in viable cell density in the absence of antibiotics, K = 2×109, fE = 10−5, gS = 10−3, gE = 10−3 per persister cell per hour. (C) Changes in viable cell density with 10 µg/ml of an antibiotic and the Hill function parameters in (A) line (1). The rest of the parameters in this and the following figure were the same as those in 1B. In this, and the following figure, the initial density of cells was 2×107 and the initial densities of PS and PE were 1/100 of that generated during the 24 hours before the start of the run. (D) Changes in total viable cell density, NT following exposure to antibiotics with different Hill function parameters and/or drug concentration. Lines (1) and (2) – Hill function in (A) line (1) with respectively 10 and 100 µg/ml of the antibiotic, Line (3) Hill function parameters in (A) line (2) and 100 µg/ml of the antibiotic, Line (4) Hill function parameters in (A) line (3) and 100 µg/ml of the antibiotic. The antibiotic kills the sensitive N cells but the initial presence and continuous production of the PS and PE persister cells prevents the total population from being cleared (Figure 1C). Because of reversion from the persisters to the N state, the sensitive population remains present. With these parameters the total population of bacteria slowly wanes as time proceeds. In Figure 1D we consider the effect of antibiotics with different properties (Hill function parameters) and concentrations on the changes in total density of viable cells, NT. There are substantial differences among drugs and concentrations in the rates at which the bacteria are killed. On the other hand, there are only modest differences in the viable cell density (primarily the density of persisters) after the population levels off. At 24 hours, the average viable cell density for 10 independent simulation runs with the most rapidly killing treatment, line (4) in Figure 1D, was 4.2×102 whilst that for treatment with the lowest rate of killing, line (1) in Figure 1D, was 5.9×102. The ratio of the standard deviation to the mean density of viable cells at 24 hours among the 10 runs was relatively low, on the order of 0.02.
Experiments
MIC estimates
In Table 1, we list the estimated MICs for the S. aureus - antibiotic combination used in the following experiments. Considering the factor of two limitation of the CLSI serial dilution protocol, the MIC estimated by both of these methods are coincident.
Tab. 1. Estimated MICs for <i>S. aureus</i> (Newman) by serial dilution and calculated from the Hill functions. 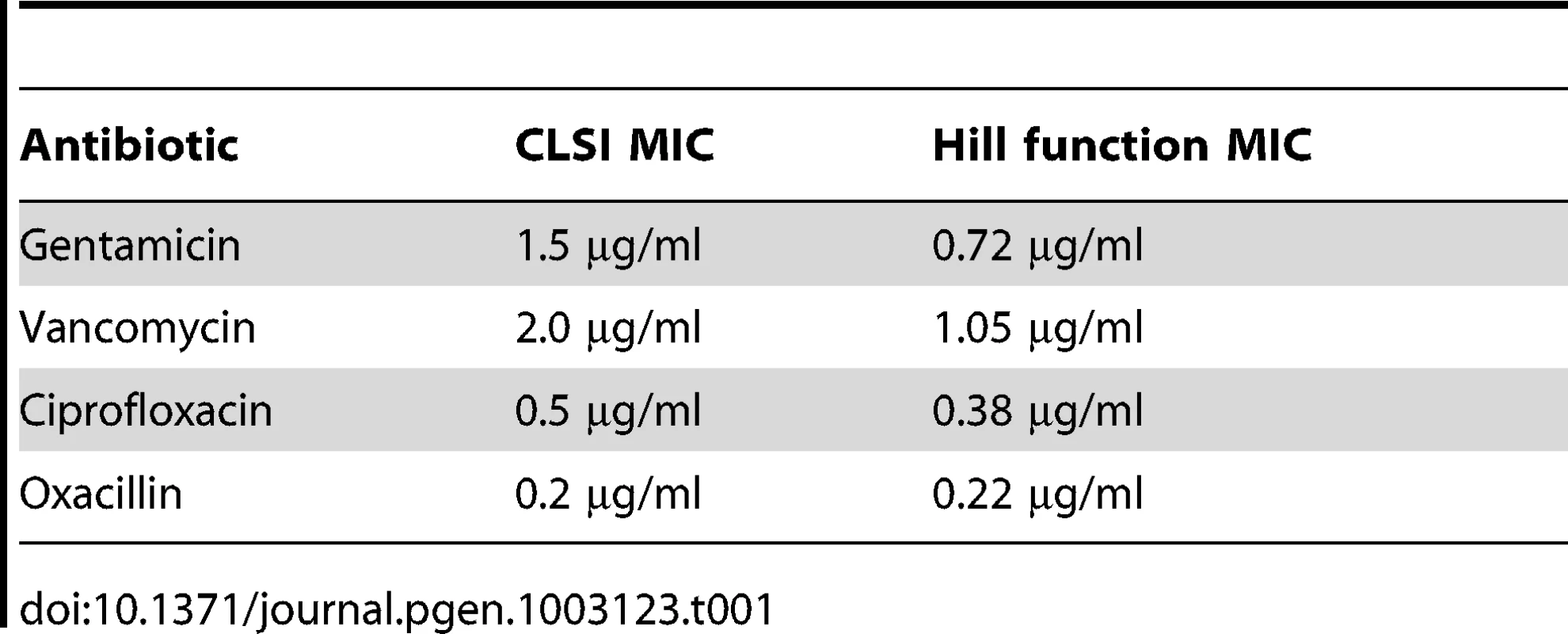
Short-term time kill—persistence level experiments
In Figure 2, we present the results of the S. aureus time kill experiments run over eight hours with frequent estimates of viable cell density. Antibiotic mediated killing starts almost immediately after ciprofloxacin and gentamicin are added to the cultures, but does not commence for about an hour after oxacillin and vancomycin are added (2 hours after the overnight cultures were diluted into fresh medium). Persistence can be seen in all cultures with above MIC concentrations of these drugs. Moreover, for ciprofloxacin and gentamicin some killing and persistence are observed for the cultures exposed to 0.5× MIC as well as supra-MIC concentrations during these eight hours. These data also suggest that the viable cell density of the persistent population may vary with the drugs and possibly their concentrations. The persistence level of cells exposed to gentamicin appears to be an order of magnitude, or more, lower than that of the other drugs.
Fig. 2. Short-term time kill experiments. 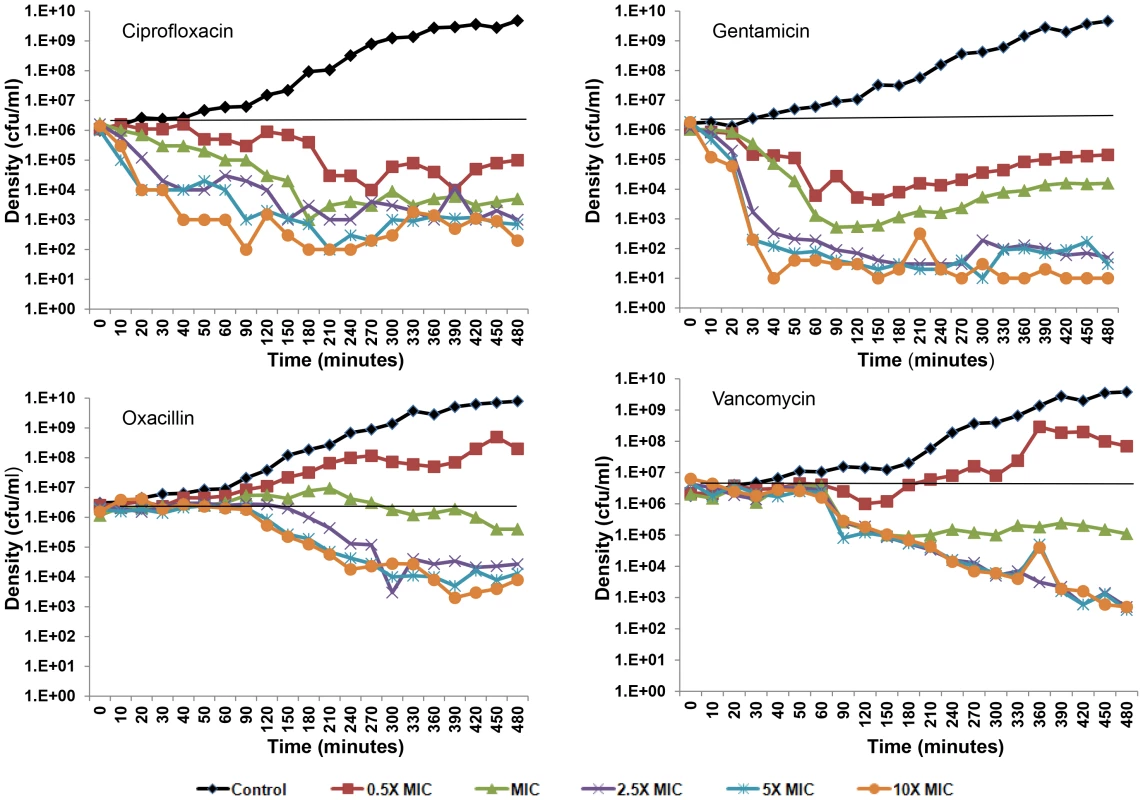
Changes in viable cell density for S. aureus Newman cultures treated with varying concentrations (0.5× MIC, MIC, 2.5× MIC, 5× MIC, and 10× MIC) of ciprofloxacin, gentamicin, oxacillin, and vancomycin. To test the hypothesis that that the cells surviving antibiotic treatment, the persisters, are only transiently refractory to antibiotics (phenotypically resistant), we conducted a second round of short term time kill experiments initiated with overnight cultures derived colonies surviving the first encounter with antibiotics. Upon re-exposure to the same concentration of each antibiotic that they were exposed to during the first time kill experiment, the persistence levels and general killing dynamics were recapitulated for all supra-MIC concentrations of antibiotics (Text S1).
Longer-term time kill—persistence level experiments
Experiments were performed to determine the relationship between the different antibiotics, their concentrations and the levels of persistence over a longer period of exposure. In the first of these longer-term persistence experiments, cultures were incubated for 12 hours with different concentrations of the four antibiotics used previously before sampling. Starting at the 12th hour, viable cell densities were estimated every two hours for the following 10 hours (Figure 3). This experiment differed from the short-term time kill experiment (Figure 2) in two ways. First, the initial density of bacteria in these longer-term cultures was greater than that we used in the short-term experiments and we only considered above MIC concentrations of the drugs. Second, we also performed three independent replicas each initiated from separate overnight cultures. It should be noted, that while in these experiments antibiotics were not added until an hour after inoculation, effectively the same final level of persistence obtains when antibiotics are added immediately (data not shown).
Fig. 3. Longer-term time kill experiments. 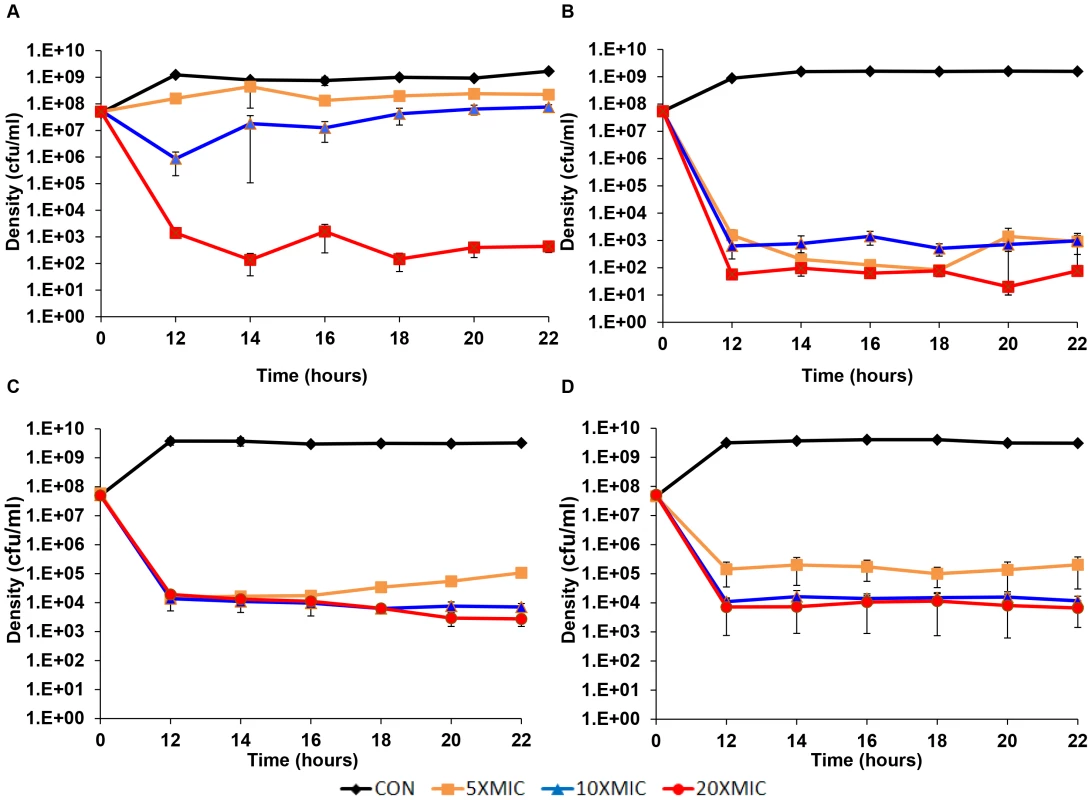
Changes in viable cell density, means and standard errors (bars), for three independent cultures of S. aureus each exposed to different concentrations (5× MIC, 10× MIC and 20× MIC) of four antibiotics: (A) Ciprofloxacin, (B) Gentamicin, (C) Oxacillin and (D) Vancomycin. The existence of a persistent subpopulation is apparent for bacteria exposed to all four drugs. For the higher concentrations of these drugs, the level of persistence seems relatively constant between 12 and 22 hours. With higher concentrations of these antibiotics, the level of persistence of the cultures treated with gentamicin and ciprofloxacin appear to be lower than that of vancomycin and oxacillin. For vancomycin, there seems to be a slight concentration effect. A concentration effect also seems to be the case for the level of persistence for oxacillin and ciprofloxacin, but see the following.
To test for inherited resistance, colonies were taken at 22 hours from these cultures, suspended in MHII broth and tested for resistance by disk diffusion assays. The only resistance observed in these assays was for the colonies recovered from the experiments with 5× and 10× MIC ciprofloxacin. Thus the seemingly higher level of persistence for these lower concentrations of this fluoroquinolone can be attributed to the evolution of bacteria that were inherently resistant to this drug. In the case of oxacillin, the higher level of persistence at lowest concentration (5× MIC) cannot be attributed to resistance, but rather appears to be due to a decline in the effective concentration of this drug. Evidence for this are the results of a bioassay, where we estimated the MIC of cell-free supernatants recovered from the 5× MIC oxacillin cultures. During the course of the 24 hours, the apparent MIC of this supernatant increased 4 fold. No significant increase in the apparent MIC was noted for the cultures with 10× and 20× MIC of oxacillin.
Antibiotic and concentration effects on the level of persistence: In an effort to better determine the effects of the nature and concentration of antibiotics on the level of persistence for two concentrations of each drug, we performed two-point time kill experiments with 10 independent replicas. For each experiment, we prepared 10 independent starting cultures, initiated with less than 5×106 cells per ml, and at times 0 and 22 hours we estimated the densities of viable cells in the cultures from CFU data. In Figure 4, we present the results of these experiments.
Fig. 4. Relative survival after 22 hours of exposure to antibiotics. 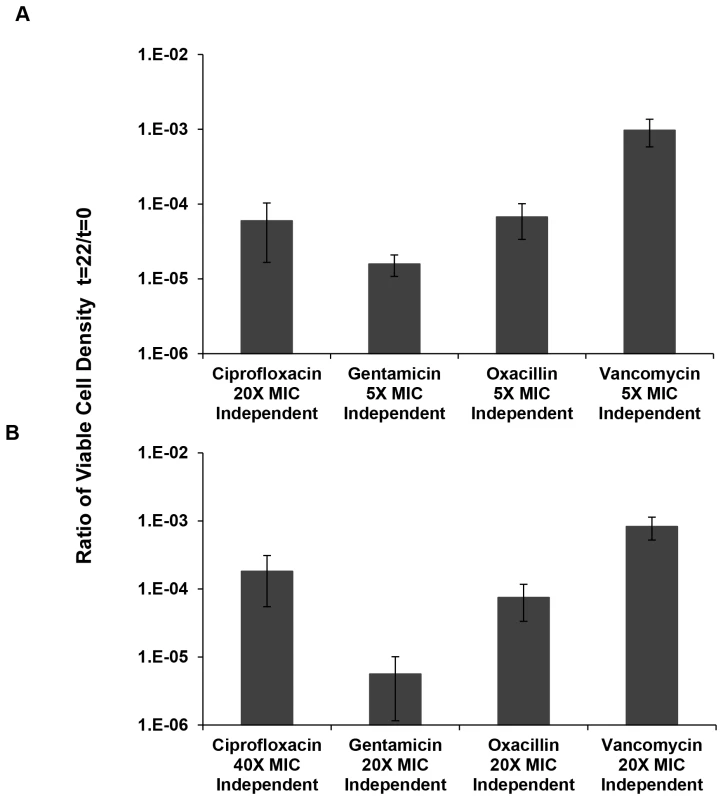
Ratio of viable cell densities (22 hours/0 hours) following treatment of 10 independent cultures of S. aureus Newman (for oxacillin and vancomycin only 9 samples are used for the calculation as we removed the extreme high numbers from each of them). (A) Mean and standard deviation of viable cell density in cultures containing “low” multiplicities of MIC for ciprofloxacin, gentamicin, oxacillin and vancomycin. (B) Mean and standard deviation of viable cell density in cultures containing “high” multiplicities of MIC for ciprofloxacin, gentamicin, oxacillin and vancomycin. Using a one-factor analysis of variance, we tested for differences in the fraction of cells surviving after 22 hours of exposure to 5× and 20× MIC of the different antibiotics relative to the initial inoculum, the persistence fraction. We did not do a 5× MIC experiment for ciprofloxacin because it was already clear that the fraction of surviving cells at this concentration was substantially greater than the other three drugs (Figure 3). Instead, we used 20× and 40× MIC in the two-point time kill experiments with this antibiotic. If we include the oxacillin survivors, the differences in viable cell densities for the 5× MIC comparison (gentamicin, oxacillin and vancomycin) were highly significant (F(2,26) = 25.6, p<0.005). If we remove oxacillin from this comparison, the between drug difference in density of persisters remains significant but less so, p<0.04 (t-test with unequal variances). For the 20× MIC comparison there were no significant differences in the level of persistence of cells exposed to the different antibiotics, F(3,34) = 1.4, p∼0.23).
For three out of the four drugs considered, gentamicin, oxacillin and vancomycin, there were significant differences between the 5× and 20× MIC survival, p<0.002 for a 2-tailed t-test with unequal variances. The level of persisters for the 20× and 40× MIC ciprofloxacin experiments were not significant, p∼0.95. But as also seen in Figure 2, at both 5× and 10× MIC of ciprofloxacin there were substantially greater numbers of surviving cells at 22 hours than at 20× MIC of ciprofloxacin.
The variance
Particularly striking in these data is the large variance in the number of persisters generated among cultures exposed to the same antibiotic. Included among these samples are cultures for which no cells were detected at minimum dilution (1/10) and cultures with more than 100 colonies. To illustrate the magnitude of this between-culture variation, we plot the standard deviation as well as the mean fraction of surviving cells for the different antibiotics in 10 independent cultures treated with different antibiotics and concentrations there-of (Figure 5).
Fig. 5. Relative survival after 22 hours of exposure to antibiotics. 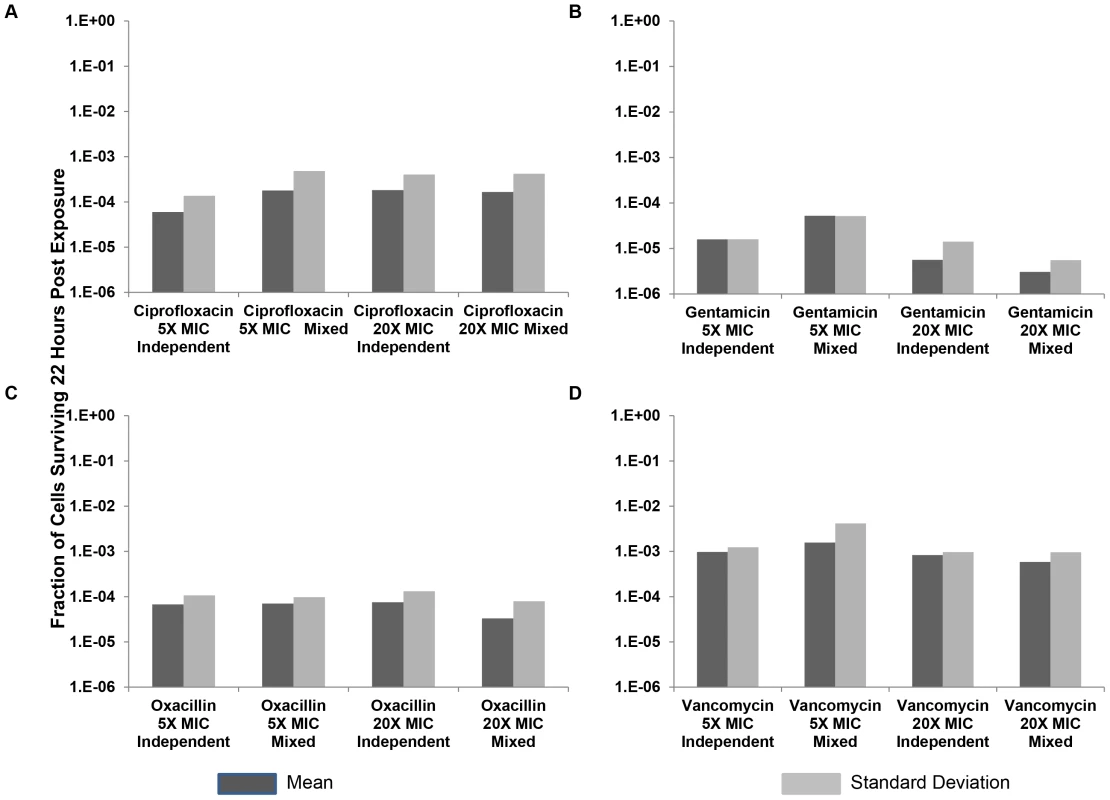
Means and standard deviations of the fraction of persisters following treatment for 10 independent cultures, and 10 cultures derived from mixtures of equal amounts of the 10 independent cultures, with either 5× MIC or 20× MIC of four antibiotics. (A) Ciprofloxacin, (B) Gentamicin, (C) Oxacillin, and (D) Vancomycin. In these experiments, the initial density of cells exposed to the antibiotics was on the order of 106 to reduce the incidence of mutants for ciprofloxacin (none were observed). To determine whether the variation in number of cells surviving exposure to the antibiotics is generated while the bacteria are growing or after they encountered the antibiotic, we performed fluctuation experiments similar to those Luria and Delbruck used to test whether mutations occur before exposure to the selective agent [36]. For this we compared the relative survival of antibiotic-exposed cells among independent cultures and cultures derived from equal volume mixtures of independent cultures. If the antibiotics only selected for pre-existing persisters, the variance in relative frequency of persisters would be substantially greater among independent cultures than the mixtures of independent cultures. The protocol for this experiment was the same as that for the experiments depicted in Figure 4. However, for the mixed cultures, equal volumes of cells from the overnight independent cultures were mixed together prior to dilution in fresh media. Following this mixing, 10 replica's were prepared in fresh media in parallel with the 10 independent cultures prepared in fresh media, allowed to grow for 1 hour, and then were incubated with either 5× or 20× MIC of their respective antibiotic for 22 hours.
As seen in Figure 5, the variation in the between culture number of persisters among the cultures that were inoculated with equal volume mixtures of individual cultures was similar to that among those inoculated with the independent cultures. This is what would be anticipated if antibiotics played a role in determining the number of persisters rather than just enriched these cultures for pre-existing persisters.
To determine the extent to which the above-described variance in the fraction of surviving cells can be attributed to variation in the ability to form colonies by the antibiotic exposed cells (plating efficiency), we plated 10 independent samples from single cultures of bacteria exposed to each of the four antibiotics. The ratios of the standard deviations to the means are respectively, 0.33, 0.10, 0.26 and 0.30 for ciprofloxacin, vancomycin, oxacillin and gentamicin. The extent of variation in the plating efficiency of antibiotic treated cultures is greater than that for the antibiotic-free control. This suggests that antibiotic exposure effects on plating efficiency accounts for some of the large variance among independent persister samples. However, the magnitude of this plating efficiency effect is far less than that which could account for the large variation among independent cultures seen in Figure 5.
A hypothesis
How do we account for the large variance in the fraction of persisters among independent and mixed cultures? As noted in the opening theoretical consideration, if antibiotics only enrich populations for existing persisters the between culture variance in the number of persisters is anticipated to be small (less than 5% of the mean) and we would not expect some cultures not to produce any persisters while others would produce many. One possible explanation is that there are few or no persisters when these independent or mixed cultures are exposed to antibiotics and these phenotypically resistant bacteria are generated after the bacteria start replicating in the presence of these drugs. If this were the case and the persisters were able to replicate at a low rate or somehow be able covert non-persisters into persisters so as a population they have a net growth rate in the presence of the antibiotic, results similar to those observed can be generated.
To illustrate the plausibility of this hypothesis in a necessarily quantitative way, we use the semi-stochastic model presented in our opening “straw person” theoretical consideration, but assume the probability of producing persisters, fe and fs is low (10−7 per cell per hour or less) and that in presence of the drug, the antibiotic refractory persisters have a maximum rate of increase of 0.2 per cell hour. The results of these simulation experiments are presented in Table 2 for four groups of 10 independent runs of antibiotics with different pharmacodynamics (Hill function parameters) and/or initial concentrations. Two related results are particularly note-worthy. First, the ratio of the standard deviation to mean number of persisters is similar to that observed in our experiments. Second, as also observed in our experiments, a number of runs terminated without persisters being detected.
Tab. 2. Simulated persister generation experiments. 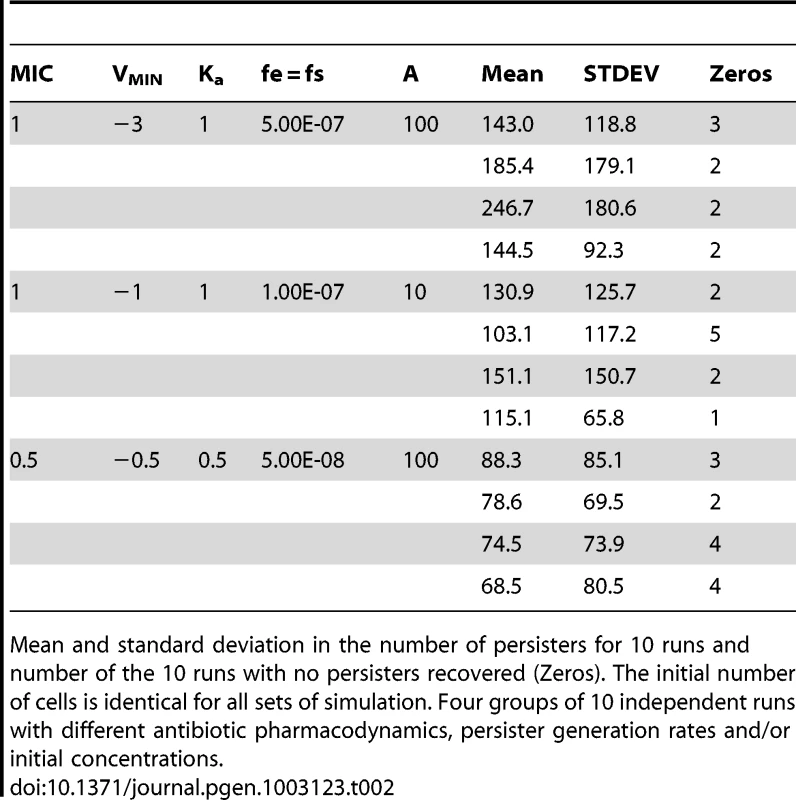
Mean and standard deviation in the number of persisters for 10 runs and number of the 10 runs with no persisters recovered (Zeros). The initial number of cells is identical for all sets of simulation. Four groups of 10 independent runs with different antibiotic pharmacodynamics, persister generation rates and/or initial concentrations. It should be emphasized that the preceding model is probably not the only mechanism that could account for the high variance between cultures in the number of persisters, the zero classes, and why mixtures of independent cultures generate similar results as independent cultures. As one reviewer of an earlier draft of this report suggested, it could well be that the different types of persisters are generated in these cultures and these vary in their ability to form colonies when exposed to antibiotics on the selecting agar. Either way, these results clearly suggest that the antibiotics play a role in determining how many persisters are produced.
Test of this hypothesis
If, as assumed above, in some way antibiotics promote the generation and/or ascent of persisters, then bacteria cultured in media with sub-MIC concentrations of antibiotics should have greater numbers of persisters than that found with unexposed bacteria. Most importantly, the number of persisters generated in these pre-treated cultures would be greater for all antibiotics, not only those to which the bacteria were pre-treated. Moreover, if this model is correct, there would be considerable between culture variations in the numbers of persisters. To test this hypothesis, we grew the bacteria with 0.2× MIC ciprofloxacin, gentamicin, vancomycin, or 0.5× MIC oxacillin and antibiotic free controls. Using the protocol employed in the preceding time-kill persister experiments, we then exposed these cultures to 20× MIC of each of the four antibiotics. The results of this experiment are presented in Figure 6.
Fig. 6. Effects of pre-exposure to sub-MIC drug concentrations on persistence levels. 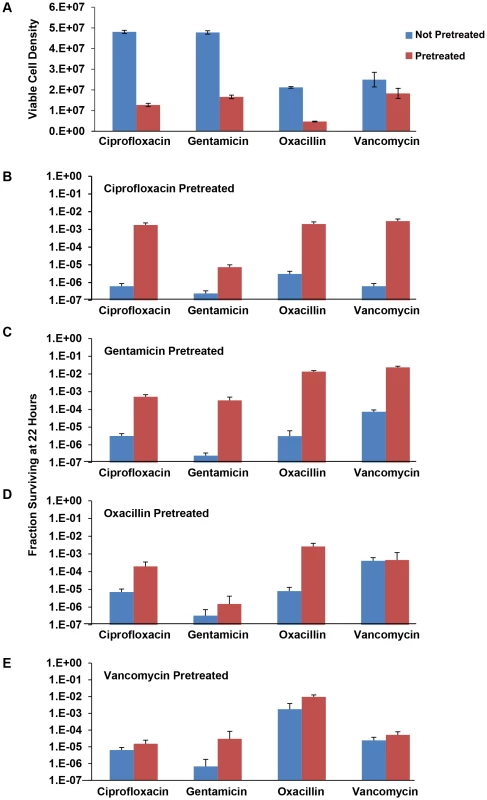
(A) Initial density of the 24 hour unexposed and antibiotic pre-treated bacteria. (B) Fraction of surviving cells (persisters) of S. aureus pre-treated with 0.2× MIC ciprofloxacin and unexposed controls after secondary treatment with 20× MIC of indicated antibiotic for 22 hours. (C) Fraction of surviving cells (persisters) of S. aureus pre-treated with 0.2× MIC gentamicin and unexposed controls after secondary treatment with 20× MIC of indicated antibiotic for 22 hours. Each data point represents the mean and standard error for 10 independent cultures. (D) Fraction of surviving cells (persisters) of S. aureus pre-treated with 0.5× MIC oxacillin and unexposed controls after secondary treatment with 20× MIC of indicated antibiotic for 22 hours. Each data point represents the mean and standard error for 10 independent cultures. (E) Fraction of surviving cells (persisters) of S. aureus pre-treated with 0.2× MIC vancomycin and unexposed controls after secondary treatment with 20× MIC of indicated antibiotic for 22 hours. Each data point represents the mean and standard error for 10 independent cultures. Although there was no evidence for difference in the turbidity of the 24-hour cultures grown in 0.2× MIC ciprofloxacin, gentamicin, and vancomycin the CFU estimates of densities were significantly lower than the corresponding controls. The turbidity of the 24-hour 0.5× MIC pre-treated oxacillin cultures however, were lower than the control cultures as were the corresponding CFU estimates. Pre-treatment with sub-MIC concentrations of ciprofloxacin and gentamicin resulted in substantial increases in the fraction of surviving cells (level of persistence) when exposed to all four antibiotics. The effects of pre-exposure to oxacillin and vancomycin, however, depended on the antibiotic used for treatment. Pre-treatment with sub-MIC concentrations of oxacillin resulted in substantial increase in the level of persistence in cultures exposed to ciprofloxacin and oxacillin but not gentamicin or vancomycin. Pre-treatment with vancomycin only augmented the level of persistence in cultures treated with gentamicin. This experiment has been performed at least twice for all the pre-treatment and treatment drugs and the same results obtained.
It should be noted that in addition to these effects of pretreatment on the level of persistence the variance in the number of persisters among cultures for the pre-exposed populations appeared to be as great as that observed earlier. That is, the ratio of the standard deviation to the mean of surviving cells in the pre-treated cultures was similar to that of the controls that were treated but not pre-treated (data not shown).
Discussion
In accord with the prevailing view, persisters are non - or slowly - growing cells generated at random from a dominant population of antibiotic susceptible bacteria. By killing growing cells, bactericidal antibiotics reveal the presence of these already existing genetically susceptible but phenotypically resistant subpopulations, but play no role in their generation and ascent. This perspective on the role of antibiotics in the generation and ascent of persisters was recently challenged by Dörr and colleague's demonstration that pre-exposure of E. coli to sub-MIC concentrations of the fluoroquinolone ciprofloxacin increases the frequency of persisters in cultures subsequently exposed to bactericidal concentrations of this drug [29]. The results presented in this jointly theoretical and experimental study with the Gram positive pathogen, Staphylococcus aureus add considerable generality to this observation. In their E. coli experiments, the only drug used for pretreatment was ciprofloxacin. Moreover the demonstration of an augmented level of persistence was also limited to a single drug, ciprofloxacin. In our experiments, pre-treatment to sub-MIC concentrations gentamicin as well as ciprofloxacin, oxacillin, and vancomycin increased the level of persistence to at least one of the four drugs used for treatment and not solely the drug used for pre-treatment. Indeed, pretreatment with ciprofloxacin and gentamicin substantially increased the level of persistence to all four drugs.
Further evidence in support of the hypothesis that antibiotics play a role in the production or ascent of persisters is the high variance in the fraction of persisters observed when independent cultures are exposed to antibiotics and the similarly high variances when mixtures of independent cultures are exposed to antibiotics. The logic behind this interpretation is the same as that which Luria and Delbruck employed [36] to distinguish between the random generation (pre-existence) of mutants and their production due to exposure to the agent selecting for their ascent. If the persisters were present before the cultures were exposed to antibiotics, contrary to what we observed there would be little variation in the number of persisters among the cultures derived from mixtures of the independent cultures. It should be noted, a high variance in the number of persisters in antibiotic treated cultures can be seen in, but was not remarked upon, earlier studies of persistence; for example, see the standard errors in Table 1 of the study by Wiuff and colleagues [20], and the error bars in Figure 1 of the investigation by Allison and collaborators [37].
In addition to providing generality and support for the proposition that antibiotics contribute to the generation and/or ascent of persisters, we also postulate and provide theoretical support for a mechanism by which antibiotics can play this role. The essence of this hypothesis is that there are few if any persisters present before the bacteria are exposed to these drugs. However, when exposed persisters are produced at a very low rate (on the order of 10−8 to 10−7) per cell per hour and, in the presence of antibiotics persisters either replicate at a low rate and/or in some way convert surviving non-persisters into persisters, see for example [38]. This mechanism however only accounts for the phenomenon of the antibiotic-associated generation of persistence at a population dynamic level. It is not founded on any specific physiological, molecular or genetic process for generating these phenotypically antibiotic resistant cells. Physiological and genetic mechanisms have, however, been postulated that could account for these results. For example, it is conceivable that these drugs induce stress responses that result in transient periods of arrested cell division [30], [39], or lead to unstable (and reversible) genetic changes, like amplification, which would then be subject to selection [40].
We do not consider the postulated population dynamic mechanism for antibiotics promoting the generation of persisters to be inconsistent with any of the hypothesis proposed for the physiological and molecular mechanisms responsible for the generation of these phenotypically - antibiotic refractory cells [24], [25], [41]–[49]. On the other hand, taken at large we believe our jointly theoretical and experimental results provide compelling support for the hypothesis that persistence can be attributed to many different mechanisms and that persisters are a diverse collection of different cell types [42].
That persistence is due to many different mechanisms [42], the majority of which are results of transient glitches and errors in the cell replication cycle or slow downs in cell metabolism, Persistence as Stuff Happens, PaSH, hypothesis can explain a variety of other observations. It provides at least two possible explanations for the different levels of persistence observed among the drugs used in the present experiments and other studies [37], [50]. First, as suggested earlier, a cell's entry into a transiently, replication - arrested, antibiotic-refractory state could be the product of a antibiotic induced stress responses [30]. The nature and extent of this stress response will almost certainly vary among drugs and their concentrations. Second, if, as suggested by [42], there are many different kinds of persister cells it is likely that the susceptibility of these bacteria to antibiotic-mediated killing would vary among drugs. An example of variation in the susceptibility of persisters to drugs has in fact been shown for some antimicrobial peptides [51].
Additional evidence in support of the PaSH hypothesis comes from essentially negative results. While there have been a number of attempts to identify the specific genes responsible for the persistence, it has not been possible to find mutants that fail to produce persisters in the surveys that have been conducted thus far [41], [52], [53], [54]. Also consistent with the PaSH hypothesis is the identification of large numbers of genes that increase or decrease frequency of persisters in different bacteria [54]. If persistence is due to different kinds of errors in cell division or reductions in rates of metabolism, it is not at all surprising that mutations in many different genes would alter the rates at which those errors occur.
An evolutionary argument
Although not direct evidence in its support, the PaSH hypothesis provides a parsimonious explanation for the existence and ubiquity of persistence. In theory and experimentally, it has been shown that if bacterial populations are periodically challenged with agents that kill growing cells, “episodic selection” [55], a population that produces persisters can be favored in competition with an otherwise higher fitness population that does not produce them [25], [55]. However, the conditions under which episodic selection will favor populations that produce persisters are restrictive. Unless the persister producing population has an intrinsic advantage, when it is rare it will not be able to invade and become established in a population that does not produce persisters or produces them at a lower rate. The reason for this is that the phenotype favored by episodic selection, a low rate of the production of non - or slow growing cells, would not be manifest if the number of the persister-producing cells is low. For example, if there were 102 persister-producing cells, N, in a population of 108 non-producers, M, and persisters are produced at a rate of 10−5 per cell per hour, the probability that there will be a single persister cell is 10−3. Although random persisters may be generated, because of their low density, the N population is more likely to eliminated by a bactericidal antibiotic rather than generate persisters, which would allow for its survival.
For a more quantitative consideration of the conditions under which episodic selection will favor the evolution and maintenance of persistence, we use an extension of our opening model of the random production of persisters for bacterial populations maintained in continuous culture. We now consider two populations of bacteria, one that produces persisters, P, and one that does not respectively N and M. The N, M populations grow at a rate proportional to the concentration of a limiting resource, R, which is consumed at a rate proportional to the maximum growth rate of the bacteria and a conversion efficiency parameter, e µg. [58], [59]. The limiting resource from a reservoir where it is maintained at a concentration, C µg/ml flows into a habitat of unit volume (1 ml) at a constant rate, w per hour which is the same rate at which excess resource, antibiotics wastes and the bacterial population, N, P and M flow out. In this model we assume the persister, P, population does not replicate or take up the resource.
In this model, persisters are generated from N cells with a single probability f per cell per hour and revert back to the N state at a rate g per cell per hour. At each hour, there is a probability, de, that AMAX µg/ml of a bacteriocidal antibiotic will be added to the vessel. In addition to being washed out at a rate w per hour the effective concentration of the antibiotic can decay at a rate da per hour. As with the model described in the body of this report, we use a Hill function for the relationship between the concentration of the antibiotic and the rate of growth/death of the bacteria. We assume the same pharmacodynamics for the N and M populations and that the persister population is totally refractory to this drug.
In our simulation, the production of persisters and the return to the N state are stochastic processes as are incidence of episodes of antibiotic introduction is stochastic processes. For this use a Monte Carlo protocol. At each time interval, Δt, the probability that a persister cell will be generated is N*f*Δt, if a random number 0<r<1 is less than this product, a persister will be added to the P population and a single cell removed from the N population. The same protocol is used for conversion of P into N, but now the probability used for comparison is P*g*Δt. For these simulations we use values of Δt and other parameters such that at any time interval these products are less than 1. At each time interval a third random number is generated. If that number is less than de*Δt, AMAX µg/ml of the antibiotic is introduced. The Berkeley Madonna program used for these is available from www.eclf.net/programs.
For each of four sets of parameters, we made 20 independent simulations each for 2000 hours. In Figure 7A we present a single simulation where the N and M populations are initially present at the same density, N = M = 5×108 (the chemostat equilibrium) and there are initially no persisters. At each episode of antibiotic treatment the viable cell density of the N and M populations decline as do that of the persisters. Although the latter are not killed by the antibiotics, their rate of production is reduced, due to the decline in N population and their reversion to the N state. They do, however, buffer the extent of decline of the N population and thereby provide the N cells an advantage, even though they grow at the same rate as the M population. This advantage of the N population also obtains when the initial frequency of N is somewhat lower than M (Figure 7B). However, when the persister producing N population is substantially rare than the M population (N = 103 and M = 109), the N population no longer has an advantage due production of antibiotic refractory persisters. Although persisters are generated by chance, their densities are too low to generate persisters and thereby prevent the elimination of the N population when confronted with the antibiotic. This threshold for density of N necessary for persistence to provide an advantage is even greater when the probability of producing persisters is lower. This can be seen in Figure 7D, where f = 10−5 rather than 10−4 per cell per hour. Under these conditions the persister-producing N population does not have an episodic selection advantage when its initial density is 105 cells per hour. More details about the outcome of the 20 independent simulations with the four sets of parameters in Figure 7 are presented in Table 3.
Fig. 7. Simulation results, episodic selection for persistence in continuous culture. 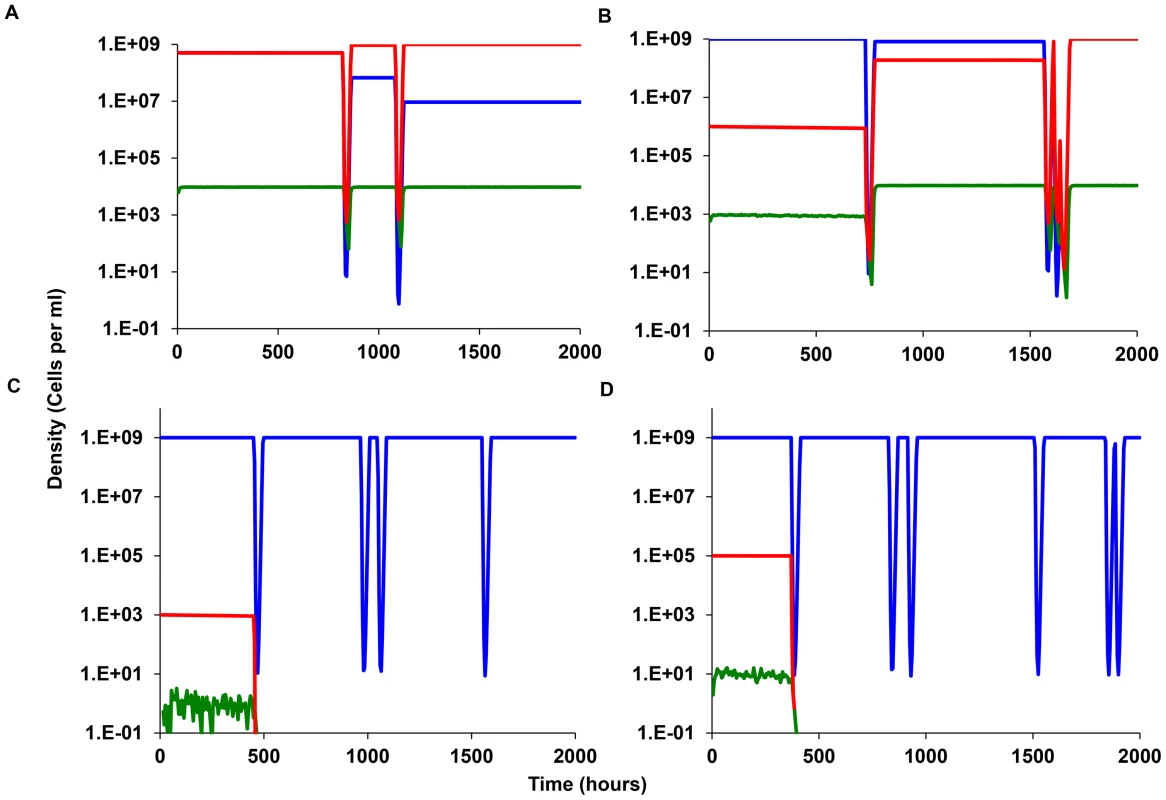
Bacteria that do and do not produce persisters, respectively N (red) and M (blue). The density of the persister population denoted by the green line. Common parameter values: g = 0.01, VMAX = 1.0, VMIN = −2.0, MIC = 1, κ = 1, epi = 0.001, and Amax = 50 µg/ml, da = 0.10 hr-1, w = 0.2 hr. for both N and M. Save for (D), f = 2×10−4 per cell per hour and in all simulations there are no persisters at time 0. (A) Changes in the density of M (blue) and N (Red) and the total persisters (Green) with initially equal densities (N = M = 5×108). (B) Same as (A) but initially N = 106 and M = 109). (C) Same as (B) but with N = 103 and M = 109 initially. (D) Same as (C) but f = 2×10−5 per cell per hour. Tab. 3. Outcomes of a series of 20 runs with the parameters in Figure 7. 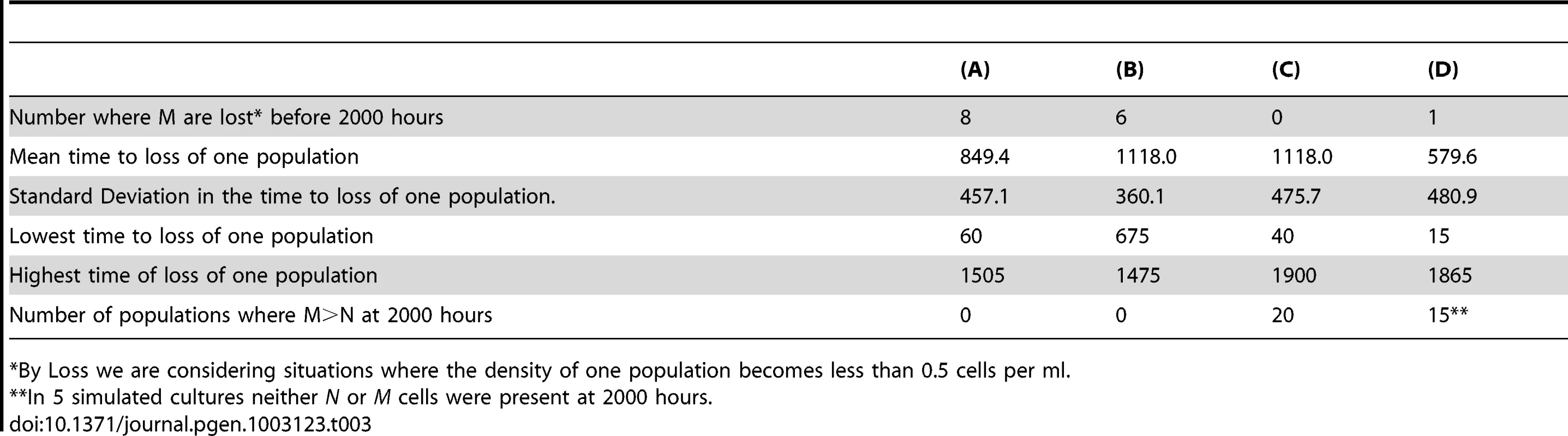
By Loss we are considering situations where the density of one population becomes less than 0.5 cells per ml. In Figure 7A, 7B, and 7C, we follow the changes in density of the persister-producing N population and it's non - producing competitor M. In Figure 7A and 7B, if in addition to producing non-growing cells, the persister producing, N population has an intrinsic disadvantage in its maximum growth rate VMAXN = 0.995, VMAXM = 1.000. In the absence of episodic selection, the relative density of the N population declines (Figure 7A). When we allow for the random introduction of a decaying antibiotic, the production of non-growing persister cells can provides the otherwise less fit persister-producing N population with an advantage. In the simulation presented in Figure 7B the population that does not produce persisters, M, is lost by 3000 hours, whilst the persister-producing N population dominates. To get a better idea of the advantage to producing non-growing, antibiotic-refractory cells, we ran this simulation 50 times and calculated the M/N ratio at 1000 hours. In 39 out of the 50 runs, the ratio of N/M exceeded 1.0. If we assume a density of 0.1 cells per ml as the cut-off for the loss of a population, the average N/M ratio at 1000 hours for the 50 runs was 3.2×109 with a standard deviation of 4.4×109 cells per ml. The lowest N/M ratio noted for the 11 runs where the M dominated was 0.15.
A very different outcome is obtained when the persister-producing N population is initially rare and the production of persisters is a random process. Although this persister-producing population has an intrinsic growth rate advantage relative to the non-producing M, it is invariably lost when its initial frequency is low (Figure 7C). The rare N population is also most commonly lost when is initial numbers are somewhat higher, 105 rather than 103 (Figure 7D). The time before the loss of the rare persister-producing population (N<0.1 per ml) varies over a large range (Table 3). The reason for this is that at these low densities, antibiotic-refractory persister cells are rarely if ever produced. And, since this population with the capacity to produce persisters is rare, even though it has a higher intrinsic fitness, it is more likely to be eliminated by the antibiotic episodes than the more common non-persister producing M, population.
If the PaSH hypothesis is correct, and persisters are largely if not exclusively the product of errors in cell replication and cell metabolism, it is no more necessary to explain the evolutionary processes responsible for the existence of persisters than it is for mutation. Like mutation, persistence is an inevitable rather than an evolved character. The high frequency persister mutants, like hipA [56], [57], are analogous to the mutants with defective mismatch and other repair genes, “mutator” genes like mutS. As is the case for mutation, evolution by natural selection can favor mechanisms that alter the rate at which these errors occur but it cannot eliminate them any more than mutator genes eliminate mutation. Because persistence is an inevitable rather than an evolved character, we would expect it to be ubiquitous. Indeed, persistence has been shown to occur in single celled eukaryotes [17], [18] as well as prokaryotes [16] and the somatic cells responsible for neoplasms [19].
Materials and Methods
Bacterial strains, antibiotics, culture, and sampling media
The experiments herein utilize Staphylococcus aureus strain Newman which was originally isolated in 1952 from a patient suffering from tubercular osteomyelitis [32]. This strain was generously provided by Dr. William Shafer. Cultures were grown in 10 mL of Mueller-Hinton II (MHII) broth in 50 mL Pyrex flasks at 37°C shaking at 200 rpm. Viable cell density per ml was determined by dilution plating on Lysogeny Broth (LB) agar (also incorrectly, but commonly, known as Luria Bertani broth or Luria Broth) [33], [34]. Antibiotic stocks were prepared to a final concentration of 10 µg/µl for ciprofloxacin, gentamicin and oxacillin while vancomycin was prepared to a final stock concentration of 15 µg/µl. All antibiotics were procured from Mediatech, Inc. (Herndon, Va.) and Sigma-Aldrich (St. Louis, Mo.). Dilutions of requisite antibiotics were made fresh in MHII broth to the appropriate concentrations for each experiment.
MICs and pharmacodynamic functions
The minimum inhibitory concentrations (MICs) of the antibiotics and bacteria used in this study were estimated with the factor of two serial dilution protocol using the method recommended by the Clinical and Laboratory Standards Institute (CLSI) [35]. In short, overnight cultures were grown in MHII, diluted to final concentrations of ∼105 in fresh media and incubated 96 well plates with two-fold serial dilutions of each antibiotic. After incubation at 37°C for 18 hours, the OD630 nm was obtained and the MICs estimated as the lowest concentration for which there was no growth. Using methods described in Regoes et al [31], we calculated the parameters of the pharmaocdymamic (Hill) functions for each combination of S. aureus and antibiotic.
Time kill and persistence assay experiments
The bacteria were grown overnight in MHII broth with shaking (200 rpm) at 37°C in 50 mL Pyrex flasks. These overnight cultures were then diluted to a final concentration of ∼2×106 or ∼2×107 bacteria (depending on assay) in fresh MHII media and incubated for 1 hour at 37°C shaking at 200 rpm to ensure entry into the exponential growth phase. Cultures were then inoculated with different concentrations (multiples of the MICs) of ciprofloxacin, gentamicin, oxacillin, or vancomycin. Densities were estimated at different times by diluting and plating on LB agar followed by incubation at 37°C for 48 hours. To control for possible confounding by antibiotic carryover on the plates, experiments were performed with a washing protocol. The antibiotic-treated cultures were centrifuged at 5,000 rpm for 6 minutes. The pellets obtained were re-suspended in fresh MHII media and pelleted again at 5,000 rpm for 6 minutes. Following the second re-suspension in fresh MHII these twice-washed cells were either plated directly, or plated following dilution in saline. While the variance in numbers of colonies observed with the washed cells was similar to those plated without washing, the estimated densities were lower, presumably because of the loss of cells or their viability during pelleting. Consequently, we elected to plate the cultures without washing.
Antimicrobial susceptibility testing
Disk diffusion (Becton, Dickinson, and Company) assays were used to test for changes in susceptibility following exposure to the antibiotics. For this, we grew individual colonies in MHII overnight and added 50 µl to 1.5 mL of LB Soft (top) agar which was then poured onto LB agar. Disks containing 5 µg ciprofloxacin, 10 µg gentamicin, 1 µg oxacillin, or 30 µg vancomycin were placed onto the plates and the plates were incubated overnight at 37°C. The following day, zones of inhibition were determined.
Supporting Information
Zdroje
1. Gonzalez-PastorJE, HobbsEC, LosickR (2003) Cannibalism by sporulating bacteria. Science 301 : 510–513.
2. DubnauD, LosickR (2006) Bistability in bacteria. Mol Microbiol 61 : 564–572.
3. ArkinA, RossJ, McAdamsHH (1998) Stochastic kinetic analysis of developmental pathway bifurcation in phage lambda-infected Escherichia coli cells. Genetics 149 : 1633–1648.
4. KaernM, ElstonTC, BlakeWJ, CollinsJJ (2005) Stochasticity in gene expression: from theories to phenotypes. Nat Rev Genet 6 : 451–464.
5. HillSA, DaviesJK (2009) Pilin gene variation in Neisseria gonorrhoeae: reassessing the old paradigms. FEMS Microbiol Rev 33 : 521–530.
6. HakanssonS, BergholmAM, HolmSE, WagnerB, WagnerM (1988) Properties of high and low density subpopulations of group B streptococci: enhanced virulence of the low density variant. Microb Pathog 5 : 345–355.
7. BiggerJW (1944) Treatment of Staphylococcal infections with penicillin. The Lancet 2 : 497–500.
8. SorianoF, GreenwoodD (1979) Action and interaction of penicillin and gentamicin on enterococci. J Clin Pathol 32 : 1174–1179.
9. MeyerK, ChaffeeE, HobbyGL, DawsonMH, SchwenkE, et al. (1942) On Penicillin. Science 96 : 20–21.
10. McDermottW (1958) Microbial persistence. Yale J Biol Med 30 : 257–291.
11. GreenwoodD, O'GradyF (1970) Trimodal response of Escherichia coli and Proteus mirabilis to penicillins. Nature 228 : 457–458.
12. PattynSR, DockxP, RollierMT, RollierR, SaerensEJ (1976) Mycobacterium leprae persisters after treatment with dapsone and rifampicin. Int J Lepr Other Mycobact Dis 44 : 154–158.
13. SinghR, BarryCE3rd, BoshoffHI (2010) The three RelE homologs of Mycobacterium tuberculosis have individual, drug-specific effects on bacterial antibiotic tolerance. J Bacteriol 192 : 1279–1291.
14. ShapiroJA, NguyenVL, ChamberlainNR (2011) Evidence for persisters in Staphylococcus epidermidis RP62a planktonic cultures and biofilms. J Med Microbiol 60 : 950–960.
15. SpoeringAL, LewisK (2001) Biofilms and planktonic cells of Pseudomonas aeruginosa have similar resistance to killing by antimicrobials. J Bacteriol 183 : 6746–6751.
16. ShahD, ZhangZ, KhodurskyA, KaldaluN, KurgK, et al. (2006) Persisters: a distinct physiological state of E. coli. BMC Microbiol 6 : 53.
17. LaFleurMD, KumamotoCA, LewisK (2006) Candida albicans biofilms produce antifungal-tolerant persister cells. Antimicrob Agents Chemother 50 : 3839–3846.
18. HarrisonJJ, TurnerRJ, CeriH (2007) A subpopulation of Candida albicans and Candida tropicalis biofilm cells are highly tolerant to chelating agents. FEMS Microbiol Lett 272 : 172–181.
19. DawsonC, IntapaC, Jabra-RizkMA (2011) “Persisters”: survival at the cellular level. PLoS Pathog 7: e1002121 doi:10.1371/journal.ppat.1002121.
20. WiuffC, ZappalaRM, RegoesRR, GarnerKN, BaqueroF, et al. (2005) Phenotypic tolerance: antibiotic enrichment of noninherited resistance in bacterial populations. Antimicrob Agents Chemother 49 : 1483–1494.
21. LevinBR, RozenDE (2006) Non-inherited antibiotic resistance. Nat Rev Microbiol 4 : 556–562.
22. MulcahyLR, BurnsJL, LoryS, LewisK (2010) Emergence of Pseudomonas aeruginosa strains producing high levels of persister cells in patients with cystic fibrosis. J Bacteriol 192 : 6191–6199.
23. LafleurMD, QiQ, LewisK (2010) Patients with long-term oral carriage harbor high-persister mutants of Candida albicans. Antimicrob Agents Chemother 54 : 39–44.
24. BalabanNQ, MerrinJ, ChaitR, KowalikL, LeiblerS (2004) Bacterial persistence as a phenotypic switch. Science 305 : 1622–1625.
25. KussellE, KishonyR, BalabanNQ, LeiblerS (2005) Bacterial persistence: a model of survival in changing environments. Genetics 169 : 1807–1814.
26. KerenI, ShahD, SpoeringA, KaldaluN, LewisK (2004) Specialized persister cells and the mechanism of multidrug tolerance in Escherichia coli. Journal of Bacteriology 186 : 8172–8180.
27. JoersA, KaldaluN, TensonT (2010) The frequency of persisters in Escherichia coli reflects the kinetics of awakening from dormancy. J Bacteriol 192 : 3379–3384.
28. GefenO, GabayC, MumcuogluM, EngelG, BalabanNQ (2008) Single-cell protein induction dynamics reveals a period of vulnerability to antibiotics in persister bacteria. Proc Natl Acad Sci U S A 105 : 6145–6149.
29. DorrT, LewisK, VulicM (2009) SOS response induces persistence to fluoroquinolones in Escherichia coli. PLoS Genet 5: e1000760 doi:10.1371/journal.pgen.1000760.
30. DorrT, VulicM, LewisK (2010) Ciprofloxacin causes persister formation by inducing the TisB toxin in Escherichia coli. PLoS Biol 8: e1000317 doi:10.1371/journal.pbio.1000317.
31. RegoesRR, WiuffC, ZappalaRM, GarnerKN, BaqueroF, et al. (2004) Pharmacodynamic functions: a multiparameter approach to the design of antibiotic treatment regimens. Antimicrob Agents Chemother 48 : 3670–3676.
32. DuthieES, LorenzLL (1952) Staphylococcal coagulase; mode of action and antigenicity. J Gen Microbiol 6 : 95–107.
33. BertaniG (1951) Studies on lysogenesis. I. The mode of phage liberation by lysogenic Escherichia coli. J Bacteriol 62 : 293–300.
34. BertaniG (2004) Lysogeny at mid-twentieth century: P1, P2, and other experimental systems. J Bacteriol 186 : 595–600.
35. Institute CaLS (2009) Methods of Dilution Antimicrobial Susceptibility Tests for Bacteria That Grow Aerobically. Vol. 29 No. 2 ed. Wayne, Pennsylvania: Clinical and Laboratory Standards Institute.
36. LuriaSE, DelbruckM (1943) Mutations of Bacteria from Virus Sensitivity to Virus Resistance. Genetics 28 : 491–511.
37. AllisonKR, BrynildsenMP, CollinsJJ (2011) Metabolite-enabled eradication of bacterial persisters by aminoglycosides. Nature 473 : 216–220.
38. VegaNM, AllisonKR, KhalilAS, CollinsJJ (2012) Signaling-mediated bacterial persister formation. Nat Chem Biol
39. FerulloDJ, LovettST (2008) The stringent response and cell cycle arrest in Escherichia coli. PLoS Genet 4: e1000300 doi:10.1371/journal.pgen.1000300.
40. GullbergE, CaoS, BergOG, IlbackC, SandegrenL, et al. (2011) Selection of resistant bacteria at very low antibiotic concentrations. PLoS Pathog 7: e1002158 doi:10.1371/journal.ppat.1002158.
41. FauvartM, De GrooteVN, MichielsJ (2011) Role of persister cells in chronic infections: clinical relevance and perspectives on anti-persister therapies. J Med Microbiol 60 : 699–709.
42. AllisonKR, BrynildsenMP, CollinsJJ (2011) Heterogeneous bacterial persisters and engineering approaches to eliminate them. Curr Opin Microbiol 14 : 593–598.
43. BalabanNQ (2011) Persistence: mechanisms for triggering and enhancing phenotypic variability. Current Opinion in Genetics & Development 21 : 768–775.
44. LewisK (2010) Persister cells. Annu Rev Microbiol 64 : 357–372.
45. LewisK (2005) Persister cells and the riddle of biofilm survival. Biochemistry (Mosc) 70 : 267–274.
46. JayaramanR (2008) Bacterial persistence: some new insights into an old phenomenon. J Biosci 33 : 795–805.
47. HansenS, LewisK, VulicM (2008) Role of global regulators and nucleotide metabolism in antibiotic tolerance in Escherichia coli. Antimicrob Agents Chemother 52 : 2718–2726.
48. Vazquez-LaslopN, LeeH, NeyfakhAA (2006) Increased persistence in Escherichia coli caused by controlled expression of toxins or other unrelated proteins. J Bacteriol 188 : 3494–3497.
49. MaisonneuveE, ShakespeareLJ, JorgensenMG, GerdesK (2011) Bacterial persistence by RNA endonucleases. Proc Natl Acad Sci U S A 108 : 13206–13211.
50. LuidaleppH, JoersA, KaldaluN, TensonT (2011) Age of inoculum strongly influences persister frequency and can mask effects of mutations implicated in altered persistence. J Bacteriol 193 : 3598–3605.
51. ChenX, ZhangM, ZhouC, KallenbachNR, RenD (2011) Control of bacterial persister cells by trp/arg-containing antimicrobial peptides. Appl Environ Microbiol 77 : 4878–4885.
52. CorreiaFF, D'OnofrioA, RejtarT, LiL, KargerBL, et al. (2006) Kinase activity of overexpressed HipA is required for growth arrest and multidrug tolerance in Escherichia coli. J Bacteriol 188 : 8360–8367.
53. SpoeringAL, VulicM, LewisK (2006) GlpD and PlsB participate in persister cell formation in Escherichia coli. J Bacteriol 188 : 5136–5144.
54. MaartinF, GrooteVD, MichielsJ (2011) Role of persister cells in chronic infections: clinical relevance and perspectives on anti-persister therapies. J Med Microbiol June 2011 60 : 699–709. J Med Microbiol 60.
55. JohnsenPJ, DubnauD, LevinBR (2009) Episodic selection and the maintenance of competence and natural transformation in Bacillus subtilis. Genetics 181 : 1521–1533.
56. MoyedHS, BertrandKP (1983) hipA, a newly recognized gene of Escherichia coli K-12 that affects frequency of persistence after inhibition of murein synthesis. J Bacteriol 155 : 768–775.
57. MoyedHS, BroderickSH (1986) Molecular cloning and expression of hipA, a gene of Escherichia coli K-12 that affects frequency of persistence after inhibition of murein synthesis. J Bacteriol 166 : 399–403.
58. MonodJ (1949) The growth of bacterial cultures. Annual Review of Microbiology 3 : 371–394.
59. StewartFM, LevinBR (1973) Resource partitioning and the outcome of interspecific competition: a model and some general considerations. American Naturalist 107 171–198.
Štítky
Genetika Reprodukčná medicína
Článek Comparative Genome Structure, Secondary Metabolite, and Effector Coding Capacity across PathogensČlánek TATES: Efficient Multivariate Genotype-Phenotype Analysis for Genome-Wide Association StudiesČlánek Secondary Metabolism and Development Is Mediated by LlmF Control of VeA Subcellular Localization inČlánek Human Disease-Associated Genetic Variation Impacts Large Intergenic Non-Coding RNA ExpressionČlánek The Roles of Whole-Genome and Small-Scale Duplications in the Functional Specialization of GenesČlánek The Role of Autophagy in Genome Stability through Suppression of Abnormal Mitosis under Starvation
Článok vyšiel v časopisePLOS Genetics
Najčítanejšie tento týždeň
2013 Číslo 1- Gynekologové a odborníci na reprodukční medicínu se sejdou na prvním virtuálním summitu
- Je „freeze-all“ pro všechny? Odborníci na fertilitu diskutovali na virtuálním summitu
-
Všetky články tohto čísla
- A Model of High Sugar Diet-Induced Cardiomyopathy
- Comparative Genome Structure, Secondary Metabolite, and Effector Coding Capacity across Pathogens
- Emerging Function of Fat Mass and Obesity-Associated Protein (Fto)
- Positional Cloning Reveals Strain-Dependent Expression of to Alter Susceptibility to Bleomycin-Induced Pulmonary Fibrosis in Mice
- Genetics of Ribosomal Proteins: “Curiouser and Curiouser”
- Transposable Elements Re-Wire and Fine-Tune the Transcriptome
- Function and Regulation of , a Gene Implicated in Autism and Human Evolution
- MAML1 Enhances the Transcriptional Activity of Runx2 and Plays a Role in Bone Development
- Predicting Mendelian Disease-Causing Non-Synonymous Single Nucleotide Variants in Exome Sequencing Studies
- A Systematic Mapping Approach of 16q12.2/ and BMI in More Than 20,000 African Americans Narrows in on the Underlying Functional Variation: Results from the Population Architecture using Genomics and Epidemiology (PAGE) Study
- Transcription of the Major microRNA–Like Small RNAs Relies on RNA Polymerase III
- Histone H3K56 Acetylation, Rad52, and Non-DNA Repair Factors Control Double-Strand Break Repair Choice with the Sister Chromatid
- Genome-Wide Association Study Identifies a Novel Susceptibility Locus at 12q23.1 for Lung Squamous Cell Carcinoma in Han Chinese
- Genetic Disruption of the Copulatory Plug in Mice Leads to Severely Reduced Fertility
- The [] Prion Exists as a Dynamic Cloud of Variants
- Adult Onset Global Loss of the Gene Alters Body Composition and Metabolism in the Mouse
- Fis Protein Insulates the Gene from Uncontrolled Transcription
- The Meiotic Nuclear Lamina Regulates Chromosome Dynamics and Promotes Efficient Homologous Recombination in the Mouse
- Genome-Wide Haplotype Analysis of Expression Quantitative Trait Loci in Monocytes
- TATES: Efficient Multivariate Genotype-Phenotype Analysis for Genome-Wide Association Studies
- Structural Basis of a Histone H3 Lysine 4 Demethylase Required for Stem Elongation in Rice
- The Ecm11-Gmc2 Complex Promotes Synaptonemal Complex Formation through Assembly of Transverse Filaments in Budding Yeast
- MCM8 Is Required for a Pathway of Meiotic Double-Strand Break Repair Independent of DMC1 in
- Comparative Genomic Analysis of the Endosymbionts of Herbivorous Insects Reveals Eco-Environmental Adaptations: Biotechnology Applications
- Integration of Nodal and BMP Signals in the Heart Requires FoxH1 to Create Left–Right Differences in Cell Migration Rates That Direct Cardiac Asymmetry
- Pharmacodynamics, Population Dynamics, and the Evolution of Persistence in
- A Hybrid Likelihood Model for Sequence-Based Disease Association Studies
- Aberration in DNA Methylation in B-Cell Lymphomas Has a Complex Origin and Increases with Disease Severity
- Multiple Opposing Constraints Govern Chromosome Interactions during Meiosis
- Transcriptional Dynamics Elicited by a Short Pulse of Notch Activation Involves Feed-Forward Regulation by Genes
- Dynamic Large-Scale Chromosomal Rearrangements Fuel Rapid Adaptation in Yeast Populations
- Heterologous Gln/Asn-Rich Proteins Impede the Propagation of Yeast Prions by Altering Chaperone Availability
- Gene Copy-Number Polymorphism Caused by Retrotransposition in Humans
- An Incompatibility between a Mitochondrial tRNA and Its Nuclear-Encoded tRNA Synthetase Compromises Development and Fitness in
- Secondary Metabolism and Development Is Mediated by LlmF Control of VeA Subcellular Localization in
- Single-Stranded Annealing Induced by Re-Initiation of Replication Origins Provides a Novel and Efficient Mechanism for Generating Copy Number Expansion via Non-Allelic Homologous Recombination
- Tbx2 Controls Lung Growth by Direct Repression of the Cell Cycle Inhibitor Genes and
- Suv4-20h Histone Methyltransferases Promote Neuroectodermal Differentiation by Silencing the Pluripotency-Associated Oct-25 Gene
- A Conserved Helicase Processivity Factor Is Needed for Conjugation and Replication of an Integrative and Conjugative Element
- Telomerase-Null Survivor Screening Identifies Novel Telomere Recombination Regulators
- Genome-Wide Analysis Reveals Selection for Important Traits in Domestic Horse Breeds
- Coordinated Degradation of Replisome Components Ensures Genome Stability upon Replication Stress in the Absence of the Replication Fork Protection Complex
- Nkx6.1 Controls a Gene Regulatory Network Required for Establishing and Maintaining Pancreatic Beta Cell Identity
- HIF- and Non-HIF-Regulated Hypoxic Responses Require the Estrogen-Related Receptor in
- Delineating a Conserved Genetic Cassette Promoting Outgrowth of Body Appendages
- The Telomere Capping Complex CST Has an Unusual Stoichiometry, Makes Multipartite Interaction with G-Tails, and Unfolds Higher-Order G-Tail Structures
- Comprehensive Methylome Characterization of and at Single-Base Resolution
- Loci Associated with -Glycosylation of Human Immunoglobulin G Show Pleiotropy with Autoimmune Diseases and Haematological Cancers
- Switchgrass Genomic Diversity, Ploidy, and Evolution: Novel Insights from a Network-Based SNP Discovery Protocol
- Centromere-Like Regions in the Budding Yeast Genome
- Sequencing of Loci from the Elephant Shark Reveals a Family of Genes in Vertebrate Genomes, Forged by Ancient Duplications and Divergences
- Mendelian and Non-Mendelian Regulation of Gene Expression in Maize
- Mutational Spectrum Drives the Rise of Mutator Bacteria
- Human Disease-Associated Genetic Variation Impacts Large Intergenic Non-Coding RNA Expression
- The Roles of Whole-Genome and Small-Scale Duplications in the Functional Specialization of Genes
- Sex-Specific Signaling in the Blood–Brain Barrier Is Required for Male Courtship in
- A Newly Uncovered Group of Distantly Related Lysine Methyltransferases Preferentially Interact with Molecular Chaperones to Regulate Their Activity
- Is Required for Leptin-Mediated Depolarization of POMC Neurons in the Hypothalamic Arcuate Nucleus in Mice
- Unlocking the Bottleneck in Forward Genetics Using Whole-Genome Sequencing and Identity by Descent to Isolate Causative Mutations
- The Role of Autophagy in Genome Stability through Suppression of Abnormal Mitosis under Starvation
- MTERF3 Regulates Mitochondrial Ribosome Biogenesis in Invertebrates and Mammals
- Downregulation and Altered Splicing by in a Mouse Model of Facioscapulohumeral Muscular Dystrophy (FSHD)
- NBR1-Mediated Selective Autophagy Targets Insoluble Ubiquitinated Protein Aggregates in Plant Stress Responses
- Retroactive Maintains Cuticle Integrity by Promoting the Trafficking of Knickkopf into the Procuticle of
- Phenome-Wide Association Study (PheWAS) for Detection of Pleiotropy within the Population Architecture using Genomics and Epidemiology (PAGE) Network
- Genetic and Functional Modularity of Activities in the Specification of Limb-Innervating Motor Neurons
- A Population Genetic Model for the Maintenance of R2 Retrotransposons in rRNA Gene Loci
- A Quartet of PIF bHLH Factors Provides a Transcriptionally Centered Signaling Hub That Regulates Seedling Morphogenesis through Differential Expression-Patterning of Shared Target Genes in
- A Genome-Wide Integrative Genomic Study Localizes Genetic Factors Influencing Antibodies against Epstein-Barr Virus Nuclear Antigen 1 (EBNA-1)
- Mutation of the Diamond-Blackfan Anemia Gene in Mouse Results in Morphological and Neuroanatomical Phenotypes
- Life, the Universe, and Everything: An Interview with David Haussler
- Alternative Oxidase Expression in the Mouse Enables Bypassing Cytochrome Oxidase Blockade and Limits Mitochondrial ROS Overproduction
- An Evolutionarily Conserved Synthetic Lethal Interaction Network Identifies FEN1 as a Broad-Spectrum Target for Anticancer Therapeutic Development
- The Flowering Repressor Underlies a Novel QTL Interacting with the Genetic Background
- Telomerase Is Required for Zebrafish Lifespan
- and Diversified Expression of the Gene Family Bolster the Floral Stem Cell Network
- Susceptibility Loci Associated with Specific and Shared Subtypes of Lymphoid Malignancies
- An Insertion in 5′ Flanking Region of Causes Blue Eggshell in the Chicken
- Increased Maternal Genome Dosage Bypasses the Requirement of the FIS Polycomb Repressive Complex 2 in Arabidopsis Seed Development
- WNK1/HSN2 Mutation in Human Peripheral Neuropathy Deregulates Expression and Posterior Lateral Line Development in Zebrafish ()
- Synergistic Interaction of Rnf8 and p53 in the Protection against Genomic Instability and Tumorigenesis
- Dot1-Dependent Histone H3K79 Methylation Promotes Activation of the Mek1 Meiotic Checkpoint Effector Kinase by Regulating the Hop1 Adaptor
- A Heterogeneous Mixture of F-Series Prostaglandins Promotes Sperm Guidance in the Reproductive Tract
- Starvation, Together with the SOS Response, Mediates High Biofilm-Specific Tolerance to the Fluoroquinolone Ofloxacin
- Directed Evolution of a Model Primordial Enzyme Provides Insights into the Development of the Genetic Code
- Genome-Wide Screens for Tinman Binding Sites Identify Cardiac Enhancers with Diverse Functional Architectures
- PLOS Genetics
- Archív čísel
- Aktuálne číslo
- Informácie o časopise
Najčítanejšie v tomto čísle- Function and Regulation of , a Gene Implicated in Autism and Human Evolution
- An Insertion in 5′ Flanking Region of Causes Blue Eggshell in the Chicken
- Comprehensive Methylome Characterization of and at Single-Base Resolution
- Susceptibility Loci Associated with Specific and Shared Subtypes of Lymphoid Malignancies
Prihlásenie#ADS_BOTTOM_SCRIPTS#Zabudnuté hesloZadajte e-mailovú adresu, s ktorou ste vytvárali účet. Budú Vám na ňu zasielané informácie k nastaveniu nového hesla.
- Časopisy





